人教版数学八年级上册14.2.2完全平方公式 课件(共19张ppt)
文档属性
| 名称 | 人教版数学八年级上册14.2.2完全平方公式 课件(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 21:25:14 | ||
图片预览






文档简介
14.2.2 完全平方公式
八年级人教版上册
课前练习:
1.计算(m+2) (m-2)=_______ (3a-2b)(3a+2b)=______
(-3-x) (3-x)=_________ (a+1) (a-1)=________
2.用代数式表示
1)a、b的平方和__________ 2) a、b的平方差________
3)a、b和的平方__________ 4) a、b差的平方_______
9a2--4b2
x2-9
a2 -1
a2+b2
a2 - b2
(a+b)2
(a-b)2
m2-4
完全平方公式的数学表达式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
你能否用代数的知识解释它的由来呢?
(a+b)2
(a-b)2
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
口诀
首平方,尾平方,两倍首尾放中央。
巧记完全平方公式:
b
b
a
a
(a+b)?
a?
b?
ab
ab
+
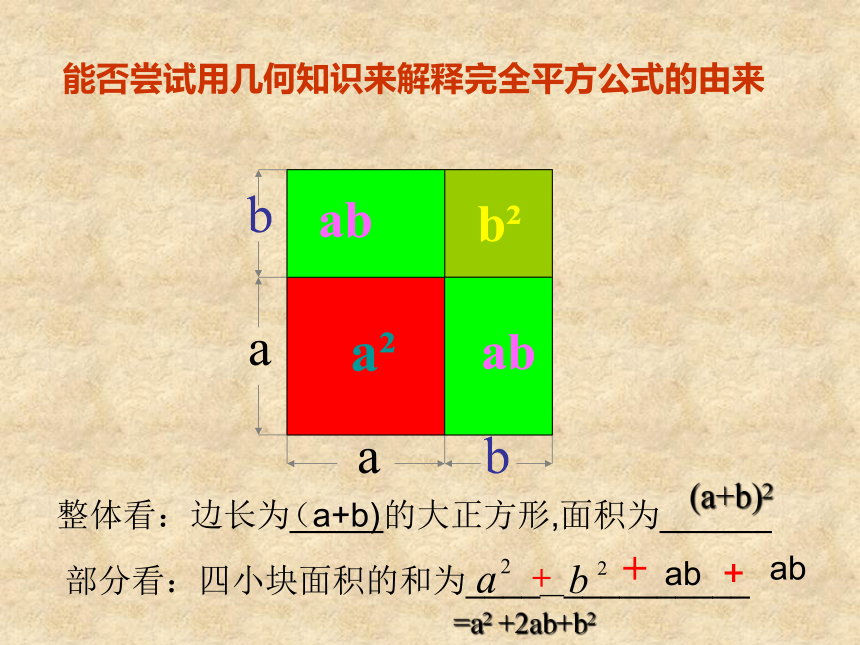
能否尝试用几何知识来解释完全平方公式的由来
整体看:边长为_____的大正方形,面积为______
部分看:四小块面积的和为________________
(a+b)
ab
+
ab
+
(a+b)2
=a2 +2ab+b2
a
a
b
b
b
b
怎样求红色阴影部分的面积?
交流合作,探索发现(二)
直接看:红色部分是边长为_______的正方形,面积为__________
(a-b)
间接看:用大正方形的面积减去其他部分的面积____________________
练一练:
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2) (x-y)2 =x2 -y2
(3) (a-b)2 =a2+2ab +b2
(4) (x+2y)2 =x2 +2xy +2y2
错
错
错
错
(x+y)2 =x2+2xy +y2
(x-y)2 =x2 -2xy+y2
(a -b)2 =a2 -2ab +b2
(x +2y)2 =x2+4xy +4y2
例3 运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 ab + b2
(4m)2
+2 · (4m) · n
+ n2
+8mn
+n2
解: (y- )2=
=y2
(2)(y - )2
(a - b)2= a2 - 2 ab + b2
y2
-2 · y ·
+( )2
-y
+
(2)1992
(1)1022
例4:利用完全平方公式计算:
解:(1)1022
= (100+2)2
=10000+400+4
=10404
(2)992
= (100 - 1)2
=10000 - 200+1
=9801
=1002+2×100×2+22
=1002-2×100×1+12
练习巩固:运用完全平方公式计算
(1)(x+6)2
(2)( y-5)2
(3)(-2x+5)2
(4)( x - y)2
(6) ( 4a2 - b2 )2
综合运用1:
计算:(a+b)(a-b)(a2 - b2)
综合运用2:
已知:a+b=3,ab=-12
求a2 +b2的值
你 难 不 倒 我
每位同学出一道要求运用完全平方公式来解的计算题。然后同位交换互测。
通过这节课的学习你学到了什么
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及
其指数;
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、公式的逆向使用;
4、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2
八年级人教版上册
课前练习:
1.计算(m+2) (m-2)=_______ (3a-2b)(3a+2b)=______
(-3-x) (3-x)=_________ (a+1) (a-1)=________
2.用代数式表示
1)a、b的平方和__________ 2) a、b的平方差________
3)a、b和的平方__________ 4) a、b差的平方_______
9a2--4b2
x2-9
a2 -1
a2+b2
a2 - b2
(a+b)2
(a-b)2
m2-4
完全平方公式的数学表达式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
你能否用代数的知识解释它的由来呢?
(a+b)2
(a-b)2
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
口诀
首平方,尾平方,两倍首尾放中央。
巧记完全平方公式:
b
b
a
a
(a+b)?
a?
b?
ab
ab
+
能否尝试用几何知识来解释完全平方公式的由来
整体看:边长为_____的大正方形,面积为______
部分看:四小块面积的和为________________
(a+b)
ab
+
ab
+
(a+b)2
=a2 +2ab+b2
a
a
b
b
b
b
怎样求红色阴影部分的面积?
交流合作,探索发现(二)
直接看:红色部分是边长为_______的正方形,面积为__________
(a-b)
间接看:用大正方形的面积减去其他部分的面积____________________
练一练:
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2) (x-y)2 =x2 -y2
(3) (a-b)2 =a2+2ab +b2
(4) (x+2y)2 =x2 +2xy +2y2
错
错
错
错
(x+y)2 =x2+2xy +y2
(x-y)2 =x2 -2xy+y2
(a -b)2 =a2 -2ab +b2
(x +2y)2 =x2+4xy +4y2
例3 运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 ab + b2
(4m)2
+2 · (4m) · n
+ n2
+8mn
+n2
解: (y- )2=
=y2
(2)(y - )2
(a - b)2= a2 - 2 ab + b2
y2
-2 · y ·
+( )2
-y
+
(2)1992
(1)1022
例4:利用完全平方公式计算:
解:(1)1022
= (100+2)2
=10000+400+4
=10404
(2)992
= (100 - 1)2
=10000 - 200+1
=9801
=1002+2×100×2+22
=1002-2×100×1+12
练习巩固:运用完全平方公式计算
(1)(x+6)2
(2)( y-5)2
(3)(-2x+5)2
(4)( x - y)2
(6) ( 4a2 - b2 )2
综合运用1:
计算:(a+b)(a-b)(a2 - b2)
综合运用2:
已知:a+b=3,ab=-12
求a2 +b2的值
你 难 不 倒 我
每位同学出一道要求运用完全平方公式来解的计算题。然后同位交换互测。
通过这节课的学习你学到了什么
小结:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及
其指数;
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
3、公式的逆向使用;
4、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2
