人教版数学九年级下册27.3 位似——在平面直角坐标系中画位似图形课件(共20张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.3 位似——在平面直角坐标系中画位似图形课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览




文档简介
27.3.2 在平面直角坐标系中画位似图形
寄语:数学并不神秘,不是只有天才才能学好数学,只要通过努力,掌握适当的方法,人人都能学会数学。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
y
x
A(1,3)
B(0,1)
C(2,1)
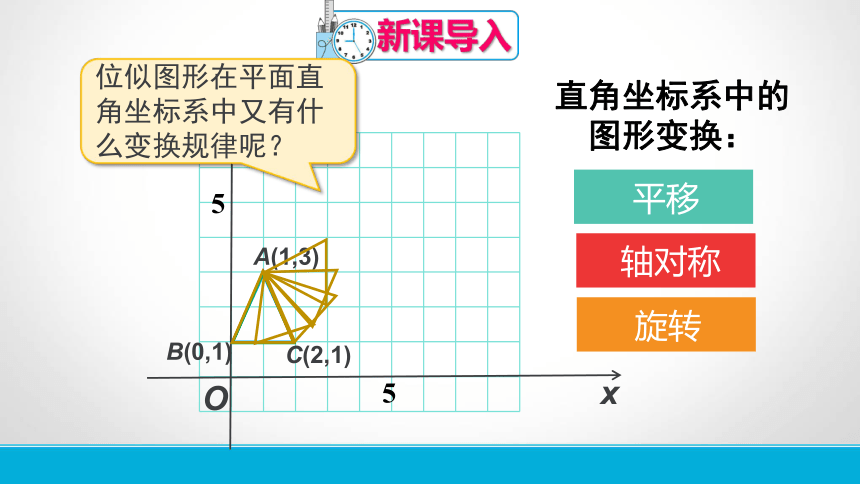
新课导入
直角坐标系中的图形变换:
平移
轴对称
旋转
5
5
位似图形在平面直角坐标系中又有什么变换规律呢?
学习目标:
(1)进一步熟悉位似的作图.
(2)会用坐标的变化来表示图形的位似变换.
(3)会根据位似图形上的点的坐标变化的规律,在坐 标系中画一个图形以原点为位似中心的位似图形.
学习重、难点:
重点:位似图形的点的坐标变化规律.
难点:以原点为位似中心的位似作图.
O
x
y
A(6,3)
5
B(6,0)
A′
B′
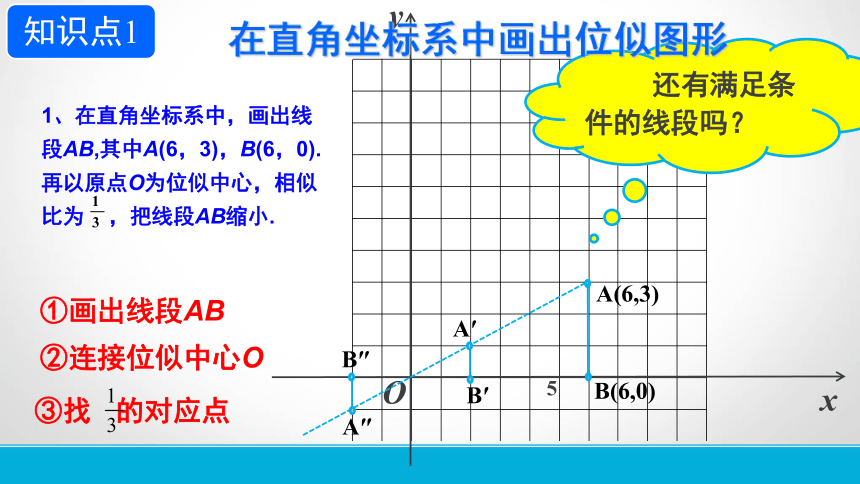
③找 的对应点
B″
A″
还有满足条件的线段吗?
1、在直角坐标系中,画出线段AB,其中A(6,3),B(6,0). 再以原点O为位似中心,相似比为 ,把线段AB缩小.
知识点1
在直角坐标系中画出位似图形
①画出线段AB
②连接位似中心O
O
x
y
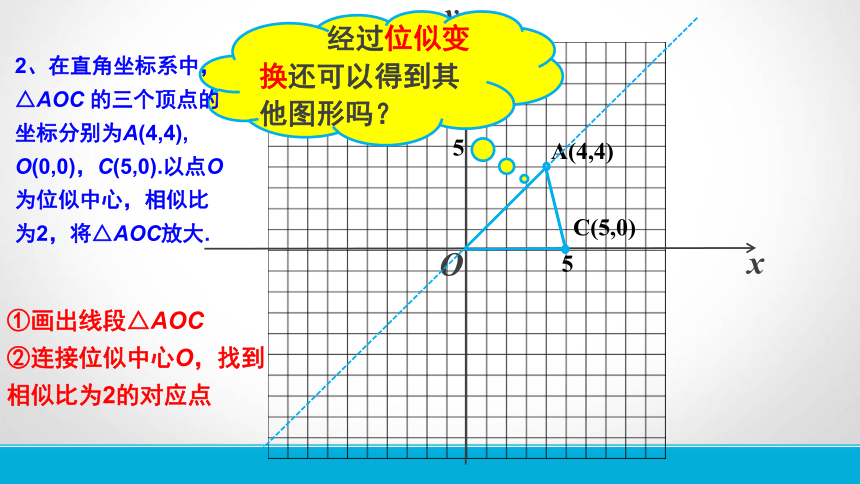
①画出线段△AOC
②连接位似中心O,找到相似比为2的对应点
A(4,4)
C(5,0)
5
5
经过位似变换还可以得到其他图形吗?
2、在直角坐标系中,△AOC 的三个顶点的坐标分别为A(4,4), O(0,0),C(5,0).以点O为位似中心,相似比为2,将△AOC放大.
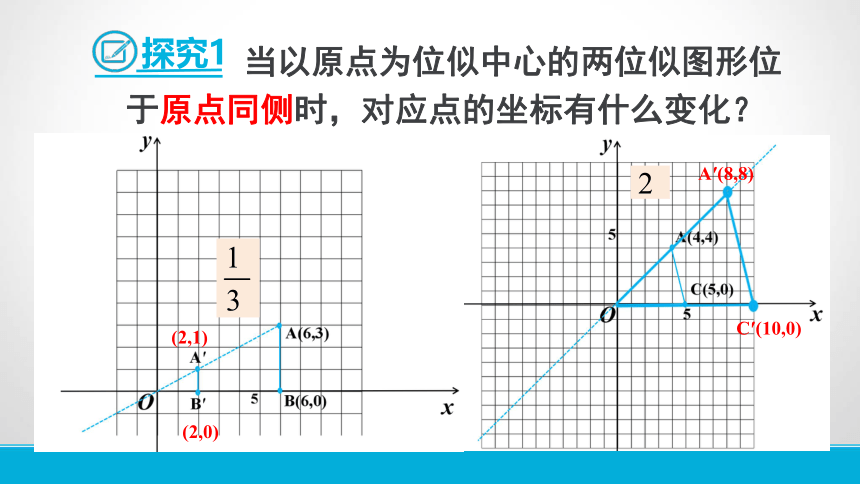
当以原点为位似中心的两位似图形位于原点同侧时,对应点的坐标有什么变化?
探究1
(2,1)
(2,0)
A′(8,8)
C′(10,0)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点同侧时,与原图形上的点(x , y)对应的位似图形上的点的坐标是 .
(kx , ky)
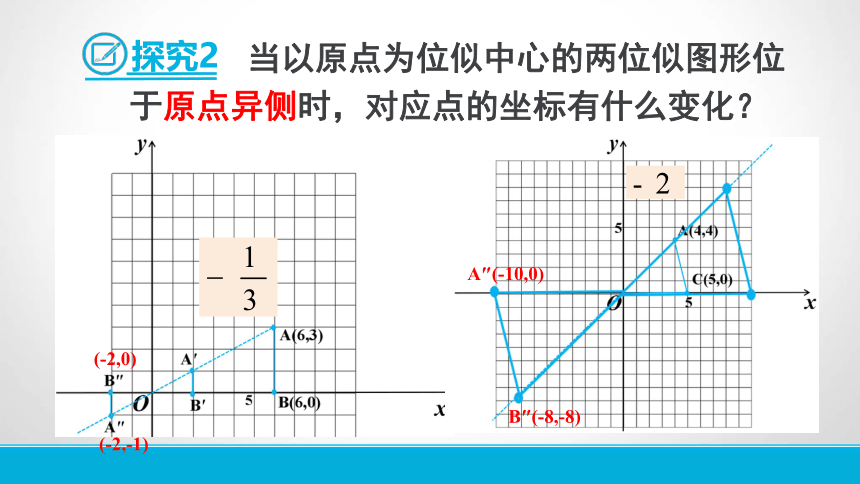
探究2
当以原点为位似中心的两位似图形位于原点异侧时,对应点的坐标有什么变化?
(-2,0)
(-2,-1)
A″(-10,0)
B″(-8,-8)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点异侧时,与原图形上的点(x , y)对应的位似图形上的点的坐标是 .
(-kx , -ky)
一般地,在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
位似图形的坐标规律
典例精析
例 如图,△ABO三个顶点的坐标分别为A(-2,4), B(-2,0), O(0,0). 以原点O为位似中心, 画出一个三角形, 使它与△ABO的
相似比为 .
{5940675A-B579-460E-94D1-54222C63F5DA}
x
O
y
-2
-4
2
2
4
6
A
B
{5940675A-B579-460E-94D1-54222C63F5DA}
x
O
y
-2
2
2
4
6
A
B
还可以得到其他图形吗?
A′(-3,6)
B′(-3,0)
A″
B″
1.如图表示△AOB和把它缩小后得到的△OCD,求△COD与△AOB的相似比。
解:相似比为OD:OB=2:5.
A
B
5
5
C
D
练习
2.如图,△ABO三个顶点的坐标分别为A(4,-5), B(6,0), O(0,0). 以原点O为位似中心,把这个三角形放大为原来的2倍,得到△A′B′O′.写出△A′B′O′三个顶点的坐标.
6
-5
A
B
6
-5
A
B
A(4,-5), B(6,0)
A′(8,-10), B′(12,0)
A″(-8,10), B″(-12,0)
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}平移、轴对称、旋转、位似变换的坐标变化规律
平移变换
轴对称变换
旋转变换
位似变换
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y 轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
一个图形绕原点旋转180° ,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数
当以原点为位似中心时,变换前后两个图形对应点的横坐标、纵坐标之比的绝对值等于相似比
课堂小结
目前已经学了哪些变换?有什么区别与联系?
平移、轴对称、旋转
还有
位似变换
位似与平移、轴对称、旋转三种变换的联系和区别:
联系:位似、平移、轴对称、旋转都是图形变换的基本形式;
区别:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(放大或缩小)变换.
1.课本第:50页 练习题1、2
2.完成课本第51页4、5
课后作业
本课时可类比上一课时的教学方式进行,只不过本课时涉及到了平面直角坐标系,教学时教师应让学生充分参与,体会平面直角坐标系的位似变换,以培养学生的动手操作能力和用位似变换解决实际问题的能力.本课的难点是用图形的坐标变化来表示图形的位似变换的变化规律,教师可让学生以小组为单位进行讨论,争取让学生自己发现规律,教师再予以适当点拨,以培养学生的探究能力.
教学反思
寄语:数学并不神秘,不是只有天才才能学好数学,只要通过努力,掌握适当的方法,人人都能学会数学。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
y
x
A(1,3)
B(0,1)
C(2,1)
新课导入
直角坐标系中的图形变换:
平移
轴对称
旋转
5
5
位似图形在平面直角坐标系中又有什么变换规律呢?
学习目标:
(1)进一步熟悉位似的作图.
(2)会用坐标的变化来表示图形的位似变换.
(3)会根据位似图形上的点的坐标变化的规律,在坐 标系中画一个图形以原点为位似中心的位似图形.
学习重、难点:
重点:位似图形的点的坐标变化规律.
难点:以原点为位似中心的位似作图.
O
x
y
A(6,3)
5
B(6,0)
A′
B′
③找 的对应点
B″
A″
还有满足条件的线段吗?
1、在直角坐标系中,画出线段AB,其中A(6,3),B(6,0). 再以原点O为位似中心,相似比为 ,把线段AB缩小.
知识点1
在直角坐标系中画出位似图形
①画出线段AB
②连接位似中心O
O
x
y
①画出线段△AOC
②连接位似中心O,找到相似比为2的对应点
A(4,4)
C(5,0)
5
5
经过位似变换还可以得到其他图形吗?
2、在直角坐标系中,△AOC 的三个顶点的坐标分别为A(4,4), O(0,0),C(5,0).以点O为位似中心,相似比为2,将△AOC放大.
当以原点为位似中心的两位似图形位于原点同侧时,对应点的坐标有什么变化?
探究1
(2,1)
(2,0)
A′(8,8)
C′(10,0)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点同侧时,与原图形上的点(x , y)对应的位似图形上的点的坐标是 .
(kx , ky)
探究2
当以原点为位似中心的两位似图形位于原点异侧时,对应点的坐标有什么变化?
(-2,0)
(-2,-1)
A″(-10,0)
B″(-8,-8)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点异侧时,与原图形上的点(x , y)对应的位似图形上的点的坐标是 .
(-kx , -ky)
一般地,在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
位似图形的坐标规律
典例精析
例 如图,△ABO三个顶点的坐标分别为A(-2,4), B(-2,0), O(0,0). 以原点O为位似中心, 画出一个三角形, 使它与△ABO的
相似比为 .
{5940675A-B579-460E-94D1-54222C63F5DA}
x
O
y
-2
-4
2
2
4
6
A
B
{5940675A-B579-460E-94D1-54222C63F5DA}
x
O
y
-2
2
2
4
6
A
B
还可以得到其他图形吗?
A′(-3,6)
B′(-3,0)
A″
B″
1.如图表示△AOB和把它缩小后得到的△OCD,求△COD与△AOB的相似比。
解:相似比为OD:OB=2:5.
A
B
5
5
C
D
练习
2.如图,△ABO三个顶点的坐标分别为A(4,-5), B(6,0), O(0,0). 以原点O为位似中心,把这个三角形放大为原来的2倍,得到△A′B′O′.写出△A′B′O′三个顶点的坐标.
6
-5
A
B
6
-5
A
B
A(4,-5), B(6,0)
A′(8,-10), B′(12,0)
A″(-8,10), B″(-12,0)
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}平移、轴对称、旋转、位似变换的坐标变化规律
平移变换
轴对称变换
旋转变换
位似变换
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y 轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
一个图形绕原点旋转180° ,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数
当以原点为位似中心时,变换前后两个图形对应点的横坐标、纵坐标之比的绝对值等于相似比
课堂小结
目前已经学了哪些变换?有什么区别与联系?
平移、轴对称、旋转
还有
位似变换
位似与平移、轴对称、旋转三种变换的联系和区别:
联系:位似、平移、轴对称、旋转都是图形变换的基本形式;
区别:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(放大或缩小)变换.
1.课本第:50页 练习题1、2
2.完成课本第51页4、5
课后作业
本课时可类比上一课时的教学方式进行,只不过本课时涉及到了平面直角坐标系,教学时教师应让学生充分参与,体会平面直角坐标系的位似变换,以培养学生的动手操作能力和用位似变换解决实际问题的能力.本课的难点是用图形的坐标变化来表示图形的位似变换的变化规律,教师可让学生以小组为单位进行讨论,争取让学生自己发现规律,教师再予以适当点拨,以培养学生的探究能力.
教学反思
