人教版数学七年级下册课件:6.3实数(第一课时)(19张)
文档属性
| 名称 | 人教版数学七年级下册课件:6.3实数(第一课时)(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 214.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:27:04 | ||
图片预览




文档简介
6.3实数(第一课时)
实数(第一课时)学习目标
1.通过把数写成小数形式后特征的分析引进无理数
2.掌握实数的概念和结构特征.
3.明确实数与数轴的关系,掌握实数比大小的方法.
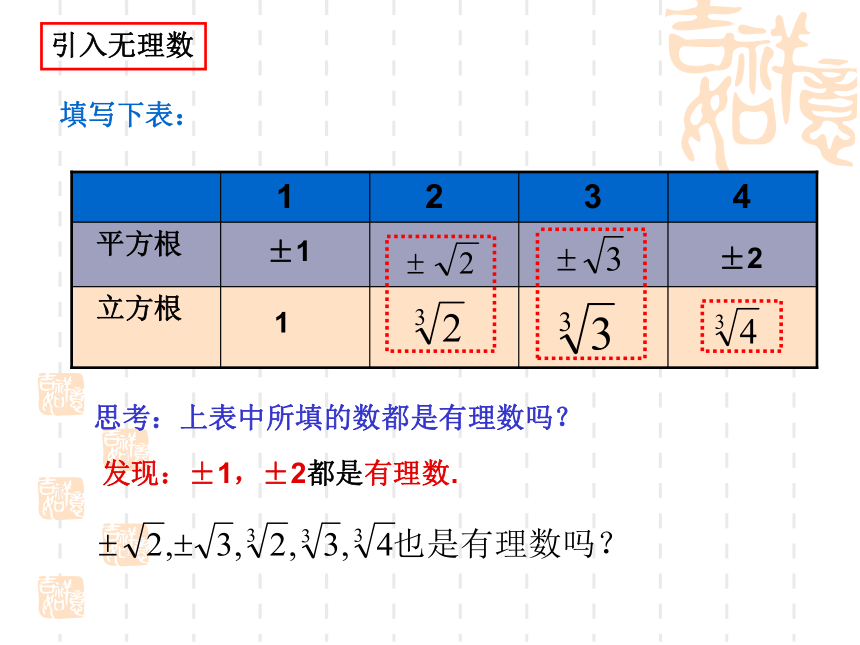
引入无理数
填写下表:
1
2
3
4
平方根
立方根
±1
±2
1
思考:上表中所填的数都是有理数吗?
发现:±1,±2都是有理数.
探索发现
写成小数观察
∏
-1
0
-1.0
0.0
-0.6
2.5
1.4142…
1.2599…
3.1415…
有理数(整数﹑分数)可以写成有限小数或无限循环小数
反过来,任何有限小数或无限循环小数也都是有理数(rationalnumber).
很多数的平方根和立方根都是无限不循环小数
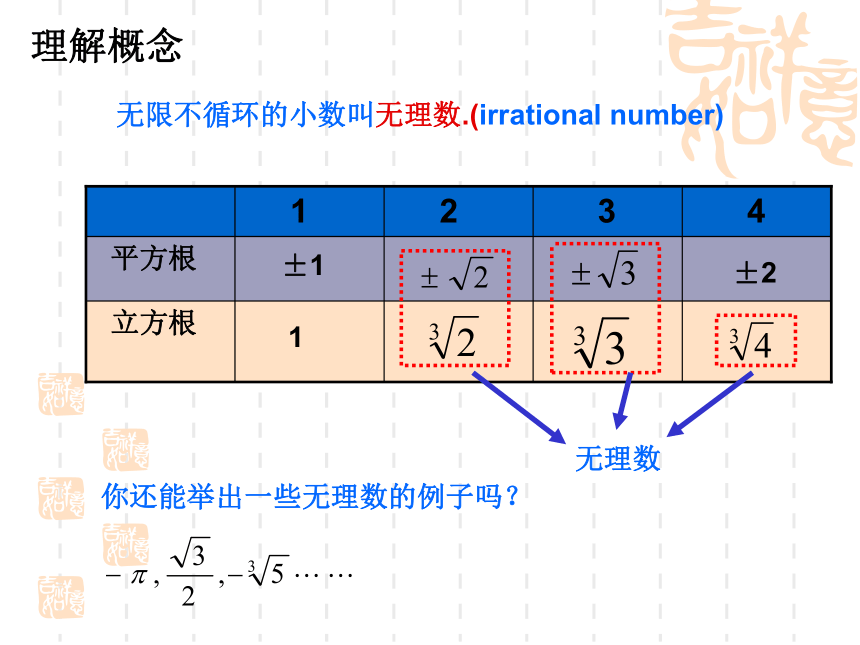
理解概念
无限不循环的小数叫无理数.(irrational number)
1
2
3
4
平方根
立方根
±1
±2
1
无理数
你还能举出一些无理数的例子吗?
巩固概念
例1 将下列各数按有理数与无理数分类.
并不是带根号的都是无理数
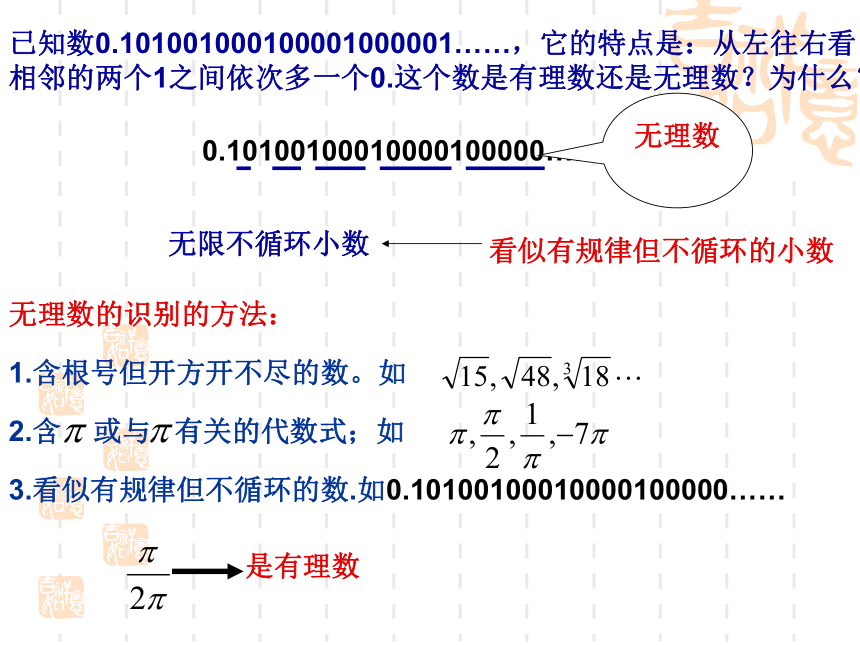
已知数0.101001000100001000001……,它的特点是:从左往右看
相邻的两个1之间依次多一个0.这个数是有理数还是无理数?为什么?
0.10100100010000100000……
无限不循环小数
看似有规律但不循环的小数
无理数
无理数的识别的方法:
1.含根号但开方开不尽的数。如
2.含 或与 有关的代数式;如
3.看似有规律但不循环的数.如0.10100100010000100000……
是有理数
概念拓展
有理数和无理数统称为实数
实
数
有理数:
有限小数或无限循环小数
无理数:
无限不循环小数
0
负实数
正无理数
实数
负有理数
正实数
正有理数
负无理数
整数
分数
1.含根号但开方开不尽的数.
2.含 ∏ 或与∏ 有关的代数式.
3.看似有规律但不循环的数.
实数与数轴
思考:每个有理数都可以用数轴上的点来表示,无理数是否
也能用数轴上的点表示出来呢?
探究:能不能在数轴上找到表示∏的点呢?
· · · · · · · ·
-3 -2 -1 0 1 2 3 4
·
直径为1的圆
∏
实数与数轴
边长为1的正方形,
对角线长为 .
· · · · · ·
-2 -1 0 1 2 3
· ·
· · · · · ·
-2 -1 0 1 2 3
· ·
· · · · · ·
-2 -1 0 1 2 3
∏
事实上,每一个无理数都可以用数轴上的点表示出来
实数与数轴上的点是一一对应的.
每一个实数都可以用数轴上的点来表示.
数轴上的每一个点都表示一个实数.
与有理数一样,实数也可以比较大小:
数轴上右边表示的实数比左边表示的实数大
· · · · · ·
-2 -1 0 1 2 3
· ·
与有理数一样,在实数范围内:
正实数大于零,负实数小于零,正实数大于一切负实数
比较大小
1.无限小数都是无理数。 ( )
2.带根号的数都是无理数. ( )
3.所有有理数都可以用数轴上的点表示,反过来,数轴上所有
点都表示有理数. ( )
×
×
×
练习1 判断
练习2
把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
练习3
……
……
有理数集合
无理数集合
在下列每一个圈里,至少填入三个适当的数.
小结归纳
有理数和无理数统称为实数
实
数
有理数:
有限小数或无限循环小数
无理数:
无限不循环小数
0
负实数
正无理数
实数
负有理数
正实数
正有理数
负无理数
整数
分数
1.含根号但开方开不尽的数.
2.含 ∏ 或与∏ 有关的代数式.
3.看似有规律但不循环的数.
1.什么是无理数、实数以及它们之间的关系
小结归纳
2.实数与数轴上的点一一对应
· · · · · ·
-2 -1 0 1 2 3
· ·
· ·
-3 4
·
-4
· ·
3.会估算与无理数接近的整数:
作业
1.教材57页习题6.3的1.2.6.7.9题
2.教材61页复习题6的6.7题
留在家校本里,要求:
1.认真书写
2.及时上传(晚9:30分之前)
3.拍照要垂直于试题,清晰
4.教师批阅后要及时订正。
实数(第一课时)学习目标
1.通过把数写成小数形式后特征的分析引进无理数
2.掌握实数的概念和结构特征.
3.明确实数与数轴的关系,掌握实数比大小的方法.
引入无理数
填写下表:
1
2
3
4
平方根
立方根
±1
±2
1
思考:上表中所填的数都是有理数吗?
发现:±1,±2都是有理数.
探索发现
写成小数观察
∏
-1
0
-1.0
0.0
-0.6
2.5
1.4142…
1.2599…
3.1415…
有理数(整数﹑分数)可以写成有限小数或无限循环小数
反过来,任何有限小数或无限循环小数也都是有理数(rationalnumber).
很多数的平方根和立方根都是无限不循环小数
理解概念
无限不循环的小数叫无理数.(irrational number)
1
2
3
4
平方根
立方根
±1
±2
1
无理数
你还能举出一些无理数的例子吗?
巩固概念
例1 将下列各数按有理数与无理数分类.
并不是带根号的都是无理数
已知数0.101001000100001000001……,它的特点是:从左往右看
相邻的两个1之间依次多一个0.这个数是有理数还是无理数?为什么?
0.10100100010000100000……
无限不循环小数
看似有规律但不循环的小数
无理数
无理数的识别的方法:
1.含根号但开方开不尽的数。如
2.含 或与 有关的代数式;如
3.看似有规律但不循环的数.如0.10100100010000100000……
是有理数
概念拓展
有理数和无理数统称为实数
实
数
有理数:
有限小数或无限循环小数
无理数:
无限不循环小数
0
负实数
正无理数
实数
负有理数
正实数
正有理数
负无理数
整数
分数
1.含根号但开方开不尽的数.
2.含 ∏ 或与∏ 有关的代数式.
3.看似有规律但不循环的数.
实数与数轴
思考:每个有理数都可以用数轴上的点来表示,无理数是否
也能用数轴上的点表示出来呢?
探究:能不能在数轴上找到表示∏的点呢?
· · · · · · · ·
-3 -2 -1 0 1 2 3 4
·
直径为1的圆
∏
实数与数轴
边长为1的正方形,
对角线长为 .
· · · · · ·
-2 -1 0 1 2 3
· ·
· · · · · ·
-2 -1 0 1 2 3
· ·
· · · · · ·
-2 -1 0 1 2 3
∏
事实上,每一个无理数都可以用数轴上的点表示出来
实数与数轴上的点是一一对应的.
每一个实数都可以用数轴上的点来表示.
数轴上的每一个点都表示一个实数.
与有理数一样,实数也可以比较大小:
数轴上右边表示的实数比左边表示的实数大
· · · · · ·
-2 -1 0 1 2 3
· ·
与有理数一样,在实数范围内:
正实数大于零,负实数小于零,正实数大于一切负实数
比较大小
1.无限小数都是无理数。 ( )
2.带根号的数都是无理数. ( )
3.所有有理数都可以用数轴上的点表示,反过来,数轴上所有
点都表示有理数. ( )
×
×
×
练习1 判断
练习2
把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
练习3
……
……
有理数集合
无理数集合
在下列每一个圈里,至少填入三个适当的数.
小结归纳
有理数和无理数统称为实数
实
数
有理数:
有限小数或无限循环小数
无理数:
无限不循环小数
0
负实数
正无理数
实数
负有理数
正实数
正有理数
负无理数
整数
分数
1.含根号但开方开不尽的数.
2.含 ∏ 或与∏ 有关的代数式.
3.看似有规律但不循环的数.
1.什么是无理数、实数以及它们之间的关系
小结归纳
2.实数与数轴上的点一一对应
· · · · · ·
-2 -1 0 1 2 3
· ·
· ·
-3 4
·
-4
· ·
3.会估算与无理数接近的整数:
作业
1.教材57页习题6.3的1.2.6.7.9题
2.教材61页复习题6的6.7题
留在家校本里,要求:
1.认真书写
2.及时上传(晚9:30分之前)
3.拍照要垂直于试题,清晰
4.教师批阅后要及时订正。
