湘教版七年级数学上册第5章《数据的收集与统计图》复习课件(共40张ppt)
文档属性
| 名称 | 湘教版七年级数学上册第5章《数据的收集与统计图》复习课件(共40张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览











文档简介
第5章数据的收集与统计图
复 习
1. 熟悉调查的两种方式及相关概念;
2. 能根据研究对象和调查目的确定恰当的调查方式;
3. 掌握各种统计图的特点,能从统计图表中提取相关信息。
4. 能制作恰当的统计图表描述数据。
5. 进一步树立数据意识,体验数形结合思想.
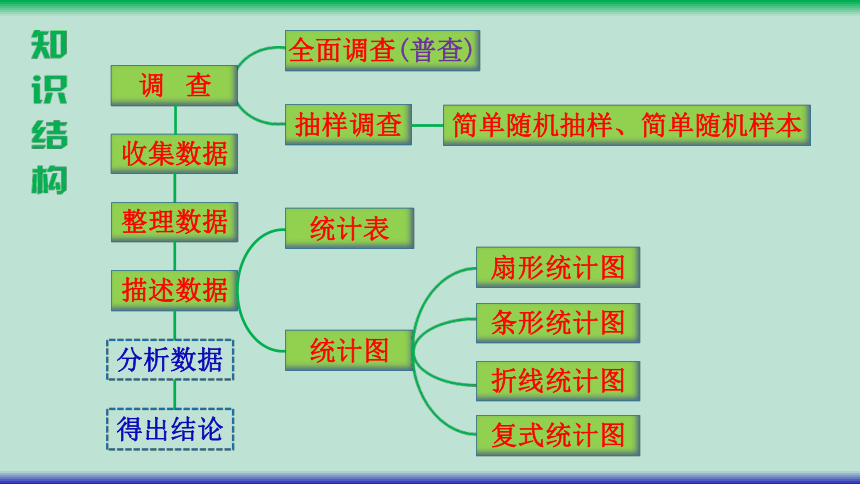
全面调查(普查)
抽样调查
简单随机抽样、简单随机样本
调 查
收集数据
整理数据
描述数据
分析数据
得出结论
统计表
统计图
扇形统计图
条形统计图
折线统计图
复式统计图
1. 研究问题,要通过 ,收集数据;收集数据之后,还要 、 、分析数据,最后得出结论。
2. 调查方式有两种: 和 。当不必要或不能进行全面调查时,采用 调查。
调查
整理数据
描述数据
全面调查
抽样调查
抽样
3. 收集的数据通过整理用 和 呈现出来.
统计表
统计图
3. 简单随机抽样要保证每个个体都有 被选入
样本。通常情况下,要使样本具有代表性,必须要选取
样本容量.
同等的机会
合适的
4. 抽取简单随机样本的方法有计算机的随机数发生器法、
抽签抽取法和 法。
按比例抽取
5. 从总体中抽取的一部分个体组成一个 ,样本
中个体的个数叫做 。
样本
样本容量
扇形统计图能清楚地表示各成分在总体中所占的百分比;
条形统计图能清楚地表示出事物的数量大小;
折线统计图能清楚地表示出事物的变化趋势;
复式统计图能清楚地对多组同性质的数据做出比较.
6. 说一说各种统计图分别有哪些特点?
7. 制作扇形统计图的三个步骤分别是什么?
第一步:计算各部分数量占总体数量的百分比;
第二步:计算各部分扇形的圆心角(百分比×360?);
第三步:画扇形统计图(画一个圆表示总体,画各个扇
形表示各部分,标出各部分占总体的百分比).
8、把多组统计数据表示在一个条形(折线)统计图上,并
标注图例,就得到 条形(折线)统计图。
9、根据 和数据的性质,选择合适的统计图。
复式
调查的目的
要点突破
(一)与调查有关的概念
例1
要了解一批电脑的内存速度,从中抽取50台电脑进行检测,在这个问题中,50是 ( )
A . 总体 B. 个体
C. 样本容量 D. 样本
C
为了了解我市140000名初中学生对“同讲普通话,携手进小康”活动的认识情况,从中随机抽取800名学生进行调查并进行统计分析,下列说法正确的是 ( )
A. 这800名学生是总体中的一个样本;
B. 我市140000名初中学生是总体;
C. 每位初中生对“同讲普通话,携手进小康”活动的认识情况
是个体;
D. 800名初中学生是样本容量。
C
下列调查中,调查方式合理的是 ( )
A. 调查洞庭湖的水质情况,采用抽样调查;
B. 对一枚火箭的零件进行检测,采用抽样调查;
C. 检验一批橘子罐头的防腐剂含量,采用全面调查;
D. 某县招聘一批新教师,对入围考生面试,采用抽样调查。
A
例2
要点突破
(二)调查方式
对下列问题的调查,最适合采用普查方式的是 ( )
A. 了解本班学生的视力情况;
B. 对一块杂交水稻试验田的水稻单穗平均结粒数的调查;
C. 对我市中学生每周课外阅读时间情况的调查;
D. 了解青少年学生对文艺明星的态度。
A
下列哪一项是复式统计图最主要的特点? ( )
A. 能清楚地看出事物的数量大小;
B. 能清楚地表示各成分在总体中所占的百分比;
C. 能清楚地对多组同性质的数据作出比较;
D. 能清楚地看出事物的变化趋势。
C
要点突破
(三)统计图的特点和选择
例3
变式题:
对某班45名学生喜欢的体育项目进行一次调查,得到下表:
为了更清楚地表示上述数据,可以制作 ( )
A. 条形统计图 B. 扇形统计图
C. 折线统计图 D. 条形统计图或扇形统计图
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}最喜欢的体育项目
乒乓球
羽毛球
篮球
足球
人数
30
20
15
10
根据右边销售量统计图,
回答问题:
(1)甲、乙两家商店这一年销售量的共同趋势是什么?
(2)你还能从图中得到什么信息?
例4
要点突破
(四)从统计图获取信息
(1)甲、乙商店这一年销售量的共同趋势是什么?
解:(1)这一年两家商店的销售高峰都在1月,而12月也是一个小高峰,同时两家商店具有共同的销售旺季和淡季.
(2)你还能从图中得到什么信息?
解:(2)第一季度甲商店的销售量低于乙商店的销售量,但甲商店的店主可能采取了一些有力的促销措施,从4月份开始,甲商店的销售量超过乙商店的销售量.
要根据统计图的特点获取信息,例如从条形统计图,可以获得数量的大小、最大值或最小值等;从折线统计图,不但可以发现事物的变化趋势,还能看出数量的大小;从扇形统计图,可以知道各成分在总体中的百分比;从复式统计图,可以对同性质的多组数据进行比较,以确定相同或不同的变化趋势及数量情况。
为培养学生的兴趣爱好好良好素质,本学期某中学准备举办科技创作、艺术特长、体育技能三个项目的素质教育活动。庞大华对全班同学所选择的活动项目进行统计,得到下表:
(1)求全班学生人数,并把表格中的数据填写完整;
(3)制作合适的统计图,表示表中人数的百分比。
例5
要点突破
(五)画统计图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}所选项目
科技创作
艺术特长
体育技能
人数
15
20
占全班人数百分比
40%
(1) 体育技能人数÷对应的百分比=全班总人数;
全班总人数×对应的百分比=各项目人数;
各项目人数÷全班总人数=对应的百分比。
(2) 要表示各项目所占百分比,选择扇形统计图比较合适.
解:(1)全班总人数:20÷40%=50(人),表格中所填数
据如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}所选项目
科技创作
艺术特长
体育技能
人数
15
15
20
占全班人数百分比
30%
30%
40%
(2)根据题意,可制作扇形统计图。
科技创作:360?×30%≈108?
艺术特长:360?×30%≈108?
体育技能:360?×40%≈144?
画出的扇形统计图如右图:
所选项目所在扇形的圆心角:
画条形、折线统计图要画好横轴和纵轴,并分别注明分别表示什么,条形统计图要根据数量画出长方形,折线统计图要注意描点;复式统计图,还要标出图例。
画扇形统计图,先计算各成分占总体的百分比,再求出对应的圆心角,最后画出各个扇形并标明各成分所占百分比。
某校为了对学生进行前途理想教育,设计调查问卷,对学生开展“将来我最想当什么”进行随机抽样调查,下面是调查后绘制的统计图(不完整):
例6
要点突破
(五)统计图的综合应用
根据上面的统计图,回答下列问题:
(1)调查了多少名学生?
(2)求出“其他”所占百分比;
(3)求出“最想当教师”的人数所占百分比;
(4)把折线统计图补充完整。
(1) 从折线统计图中找出“军人40人”,再在扇形统计图中找出40的对应百分比,用除法计算即可求出调查了多少人;
(2)用“其他”人数除以调查了的总人数;
(3)用“1”减去各成分所占百分比;
(4)用调查了的总人数分别乘“教师”、“医生”所占百分比,得出“教师”“医生”人数,然后把折线图补充完整。
解:(1)调查了的人数:40÷16%=250(人)。
(2)“其他”所占百分比:80÷250=32%。
(3)“教师”所占百分比:1-(16%+32%+24%+18%)=10%.
(4)教师人数:250×10%=25(人),
公务员人数:250×18%=45(人),(图略)。
画条形、折线统计图要画好横轴和纵轴,并分别注明分别表示什么,条形统计图要根据数量画出长方形,折线统计图要注意描点;复式统计图,还要标出图例。
画扇形统计图,先计算各成分占总体的百分比,再求出对应的圆心角,最后画出各个扇形并标明各成分所占百分比。
●基础巩固题
1.下面说法中正确的是 ( )
A.样本中个体的个数叫做总体
B. 考察对象的总个数叫做总体
C. 总体的一部分叫个体
D. 从总体中抽取的一部分个体叫总体的一个样本.
D
2.为了解一次七年级数学考试成绩,从2000名学生的成绩中抽取了一部分,其中2人得100分,3人得98分,5人得94分,12人得90分,15人得82分,23人得76分,在这个问题中,样本容量是 .
60
3.隆回县教育局为了解学生对学校推行素质教育的看法,
应采用的最佳调查方式是 ( )
A. 对所有学校进行全面调查
B. 对县内两所省示范性高中进行调查
C. 对城区随机抽取1所小学、1所初中和1所高中进行调查
D. 按8%的比例在城区和农村随机抽取若干所小学、初中
和高中进行调查.
D
4. 空气质量是天气预报的一项重要内容。要描述某市在一个月
内空气质量的变化情况,应当绘制 ( )
A. 条形统计图 B. 扇形统计图
C. 折线统计图 D. 条形统计图或扇形统计图
C
5. 如图是某粮店仓库的贮藏情况统计图,已知仓库中有玉米8
吨, 那么其中大米有 吨,小麦 吨。
24
40
6. 某校在“艺术节”活动中,根据各年级参赛节目数,绘制
了如下扇形统计图。小敏只知道七年级共有18个节目,
小锐说他能算出八、九年
的参赛节目数。小锐算出
九年级参赛的节目个数是
.
24
7.张老师对班上期中考试的成绩进行统计,绘制了如下统计
图,根据图中给出的信息,可知本次考试达到A等和B等
成绩的人数占全班的 ( )
A. 24%
B. 26%
C. 48%
D. 52%
D
8.下图是根据某市2014至2019年工业生产总值绘制的折线统计
图,下列判断不正确的是 ( )
A. 2014至2019年工业生产
总值逐年增加;
B. 2017至2019年每年工业
生产总值增长速度相同;
C. 增长速度最快是2016年;
D. 2014至2018年工业生产
总值共增加80万元.
D
●综合运用题
9. 在2020年荷香桥镇中心校“读书沙龙及师德宣讲活动”竞赛中,共评出一等奖15名、二等奖25名、三等奖40名.
(1) 分别求出获一、二、三等奖人数占获奖总人数的百分比;
(2) 制作恰当的统计图,表示上面求得的百分比.
10. 交通部门随机抽样调查了某单位职工上下班的交通方式,
绘制了如下两幅统计图:
根据统计图的信息,解答问题:
(1) m= ;
(2) 补全条形统计图;
(3) 求出扇形统计图中“乘公交车”所占百分比;
(4) 该单位共有1000人,倡导“低碳生活,绿色出行”一段时间后,步行和乘公交车上班的人数保持不变,坐私家车的人数与骑自行车的人数相等,原来坐私家车的人中有多少人改成了骑自行车?
解:(1)调查总人数:24÷12%=200(人);m=200×28%=56;
(2)骑自行车的人数:200×24%=48(人),图略;
(3)1-(12%+24%+28%)=36%;
(4)该单位坐私家车和骑自行车的总人数为:
1000×(28%+24%)=520(人)。
原来坐私家车的人数:1000×28%=280(人)。
现在坐私家车的人数:520÷2=260(人)。
坐私家车改为骑自行车的人数:280-260=20(人)。
复 习
1. 熟悉调查的两种方式及相关概念;
2. 能根据研究对象和调查目的确定恰当的调查方式;
3. 掌握各种统计图的特点,能从统计图表中提取相关信息。
4. 能制作恰当的统计图表描述数据。
5. 进一步树立数据意识,体验数形结合思想.
全面调查(普查)
抽样调查
简单随机抽样、简单随机样本
调 查
收集数据
整理数据
描述数据
分析数据
得出结论
统计表
统计图
扇形统计图
条形统计图
折线统计图
复式统计图
1. 研究问题,要通过 ,收集数据;收集数据之后,还要 、 、分析数据,最后得出结论。
2. 调查方式有两种: 和 。当不必要或不能进行全面调查时,采用 调查。
调查
整理数据
描述数据
全面调查
抽样调查
抽样
3. 收集的数据通过整理用 和 呈现出来.
统计表
统计图
3. 简单随机抽样要保证每个个体都有 被选入
样本。通常情况下,要使样本具有代表性,必须要选取
样本容量.
同等的机会
合适的
4. 抽取简单随机样本的方法有计算机的随机数发生器法、
抽签抽取法和 法。
按比例抽取
5. 从总体中抽取的一部分个体组成一个 ,样本
中个体的个数叫做 。
样本
样本容量
扇形统计图能清楚地表示各成分在总体中所占的百分比;
条形统计图能清楚地表示出事物的数量大小;
折线统计图能清楚地表示出事物的变化趋势;
复式统计图能清楚地对多组同性质的数据做出比较.
6. 说一说各种统计图分别有哪些特点?
7. 制作扇形统计图的三个步骤分别是什么?
第一步:计算各部分数量占总体数量的百分比;
第二步:计算各部分扇形的圆心角(百分比×360?);
第三步:画扇形统计图(画一个圆表示总体,画各个扇
形表示各部分,标出各部分占总体的百分比).
8、把多组统计数据表示在一个条形(折线)统计图上,并
标注图例,就得到 条形(折线)统计图。
9、根据 和数据的性质,选择合适的统计图。
复式
调查的目的
要点突破
(一)与调查有关的概念
例1
要了解一批电脑的内存速度,从中抽取50台电脑进行检测,在这个问题中,50是 ( )
A . 总体 B. 个体
C. 样本容量 D. 样本
C
为了了解我市140000名初中学生对“同讲普通话,携手进小康”活动的认识情况,从中随机抽取800名学生进行调查并进行统计分析,下列说法正确的是 ( )
A. 这800名学生是总体中的一个样本;
B. 我市140000名初中学生是总体;
C. 每位初中生对“同讲普通话,携手进小康”活动的认识情况
是个体;
D. 800名初中学生是样本容量。
C
下列调查中,调查方式合理的是 ( )
A. 调查洞庭湖的水质情况,采用抽样调查;
B. 对一枚火箭的零件进行检测,采用抽样调查;
C. 检验一批橘子罐头的防腐剂含量,采用全面调查;
D. 某县招聘一批新教师,对入围考生面试,采用抽样调查。
A
例2
要点突破
(二)调查方式
对下列问题的调查,最适合采用普查方式的是 ( )
A. 了解本班学生的视力情况;
B. 对一块杂交水稻试验田的水稻单穗平均结粒数的调查;
C. 对我市中学生每周课外阅读时间情况的调查;
D. 了解青少年学生对文艺明星的态度。
A
下列哪一项是复式统计图最主要的特点? ( )
A. 能清楚地看出事物的数量大小;
B. 能清楚地表示各成分在总体中所占的百分比;
C. 能清楚地对多组同性质的数据作出比较;
D. 能清楚地看出事物的变化趋势。
C
要点突破
(三)统计图的特点和选择
例3
变式题:
对某班45名学生喜欢的体育项目进行一次调查,得到下表:
为了更清楚地表示上述数据,可以制作 ( )
A. 条形统计图 B. 扇形统计图
C. 折线统计图 D. 条形统计图或扇形统计图
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}最喜欢的体育项目
乒乓球
羽毛球
篮球
足球
人数
30
20
15
10
根据右边销售量统计图,
回答问题:
(1)甲、乙两家商店这一年销售量的共同趋势是什么?
(2)你还能从图中得到什么信息?
例4
要点突破
(四)从统计图获取信息
(1)甲、乙商店这一年销售量的共同趋势是什么?
解:(1)这一年两家商店的销售高峰都在1月,而12月也是一个小高峰,同时两家商店具有共同的销售旺季和淡季.
(2)你还能从图中得到什么信息?
解:(2)第一季度甲商店的销售量低于乙商店的销售量,但甲商店的店主可能采取了一些有力的促销措施,从4月份开始,甲商店的销售量超过乙商店的销售量.
要根据统计图的特点获取信息,例如从条形统计图,可以获得数量的大小、最大值或最小值等;从折线统计图,不但可以发现事物的变化趋势,还能看出数量的大小;从扇形统计图,可以知道各成分在总体中的百分比;从复式统计图,可以对同性质的多组数据进行比较,以确定相同或不同的变化趋势及数量情况。
为培养学生的兴趣爱好好良好素质,本学期某中学准备举办科技创作、艺术特长、体育技能三个项目的素质教育活动。庞大华对全班同学所选择的活动项目进行统计,得到下表:
(1)求全班学生人数,并把表格中的数据填写完整;
(3)制作合适的统计图,表示表中人数的百分比。
例5
要点突破
(五)画统计图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}所选项目
科技创作
艺术特长
体育技能
人数
15
20
占全班人数百分比
40%
(1) 体育技能人数÷对应的百分比=全班总人数;
全班总人数×对应的百分比=各项目人数;
各项目人数÷全班总人数=对应的百分比。
(2) 要表示各项目所占百分比,选择扇形统计图比较合适.
解:(1)全班总人数:20÷40%=50(人),表格中所填数
据如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}所选项目
科技创作
艺术特长
体育技能
人数
15
15
20
占全班人数百分比
30%
30%
40%
(2)根据题意,可制作扇形统计图。
科技创作:360?×30%≈108?
艺术特长:360?×30%≈108?
体育技能:360?×40%≈144?
画出的扇形统计图如右图:
所选项目所在扇形的圆心角:
画条形、折线统计图要画好横轴和纵轴,并分别注明分别表示什么,条形统计图要根据数量画出长方形,折线统计图要注意描点;复式统计图,还要标出图例。
画扇形统计图,先计算各成分占总体的百分比,再求出对应的圆心角,最后画出各个扇形并标明各成分所占百分比。
某校为了对学生进行前途理想教育,设计调查问卷,对学生开展“将来我最想当什么”进行随机抽样调查,下面是调查后绘制的统计图(不完整):
例6
要点突破
(五)统计图的综合应用
根据上面的统计图,回答下列问题:
(1)调查了多少名学生?
(2)求出“其他”所占百分比;
(3)求出“最想当教师”的人数所占百分比;
(4)把折线统计图补充完整。
(1) 从折线统计图中找出“军人40人”,再在扇形统计图中找出40的对应百分比,用除法计算即可求出调查了多少人;
(2)用“其他”人数除以调查了的总人数;
(3)用“1”减去各成分所占百分比;
(4)用调查了的总人数分别乘“教师”、“医生”所占百分比,得出“教师”“医生”人数,然后把折线图补充完整。
解:(1)调查了的人数:40÷16%=250(人)。
(2)“其他”所占百分比:80÷250=32%。
(3)“教师”所占百分比:1-(16%+32%+24%+18%)=10%.
(4)教师人数:250×10%=25(人),
公务员人数:250×18%=45(人),(图略)。
画条形、折线统计图要画好横轴和纵轴,并分别注明分别表示什么,条形统计图要根据数量画出长方形,折线统计图要注意描点;复式统计图,还要标出图例。
画扇形统计图,先计算各成分占总体的百分比,再求出对应的圆心角,最后画出各个扇形并标明各成分所占百分比。
●基础巩固题
1.下面说法中正确的是 ( )
A.样本中个体的个数叫做总体
B. 考察对象的总个数叫做总体
C. 总体的一部分叫个体
D. 从总体中抽取的一部分个体叫总体的一个样本.
D
2.为了解一次七年级数学考试成绩,从2000名学生的成绩中抽取了一部分,其中2人得100分,3人得98分,5人得94分,12人得90分,15人得82分,23人得76分,在这个问题中,样本容量是 .
60
3.隆回县教育局为了解学生对学校推行素质教育的看法,
应采用的最佳调查方式是 ( )
A. 对所有学校进行全面调查
B. 对县内两所省示范性高中进行调查
C. 对城区随机抽取1所小学、1所初中和1所高中进行调查
D. 按8%的比例在城区和农村随机抽取若干所小学、初中
和高中进行调查.
D
4. 空气质量是天气预报的一项重要内容。要描述某市在一个月
内空气质量的变化情况,应当绘制 ( )
A. 条形统计图 B. 扇形统计图
C. 折线统计图 D. 条形统计图或扇形统计图
C
5. 如图是某粮店仓库的贮藏情况统计图,已知仓库中有玉米8
吨, 那么其中大米有 吨,小麦 吨。
24
40
6. 某校在“艺术节”活动中,根据各年级参赛节目数,绘制
了如下扇形统计图。小敏只知道七年级共有18个节目,
小锐说他能算出八、九年
的参赛节目数。小锐算出
九年级参赛的节目个数是
.
24
7.张老师对班上期中考试的成绩进行统计,绘制了如下统计
图,根据图中给出的信息,可知本次考试达到A等和B等
成绩的人数占全班的 ( )
A. 24%
B. 26%
C. 48%
D. 52%
D
8.下图是根据某市2014至2019年工业生产总值绘制的折线统计
图,下列判断不正确的是 ( )
A. 2014至2019年工业生产
总值逐年增加;
B. 2017至2019年每年工业
生产总值增长速度相同;
C. 增长速度最快是2016年;
D. 2014至2018年工业生产
总值共增加80万元.
D
●综合运用题
9. 在2020年荷香桥镇中心校“读书沙龙及师德宣讲活动”竞赛中,共评出一等奖15名、二等奖25名、三等奖40名.
(1) 分别求出获一、二、三等奖人数占获奖总人数的百分比;
(2) 制作恰当的统计图,表示上面求得的百分比.
10. 交通部门随机抽样调查了某单位职工上下班的交通方式,
绘制了如下两幅统计图:
根据统计图的信息,解答问题:
(1) m= ;
(2) 补全条形统计图;
(3) 求出扇形统计图中“乘公交车”所占百分比;
(4) 该单位共有1000人,倡导“低碳生活,绿色出行”一段时间后,步行和乘公交车上班的人数保持不变,坐私家车的人数与骑自行车的人数相等,原来坐私家车的人中有多少人改成了骑自行车?
解:(1)调查总人数:24÷12%=200(人);m=200×28%=56;
(2)骑自行车的人数:200×24%=48(人),图略;
(3)1-(12%+24%+28%)=36%;
(4)该单位坐私家车和骑自行车的总人数为:
1000×(28%+24%)=520(人)。
原来坐私家车的人数:1000×28%=280(人)。
现在坐私家车的人数:520÷2=260(人)。
坐私家车改为骑自行车的人数:280-260=20(人)。
同课章节目录
