1.2空间几何体的三视图与直观图 专题训练(含答案)
文档属性
| 名称 | 1.2空间几何体的三视图与直观图 专题训练(含答案) |  | |
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:26:24 | ||
图片预览


文档简介
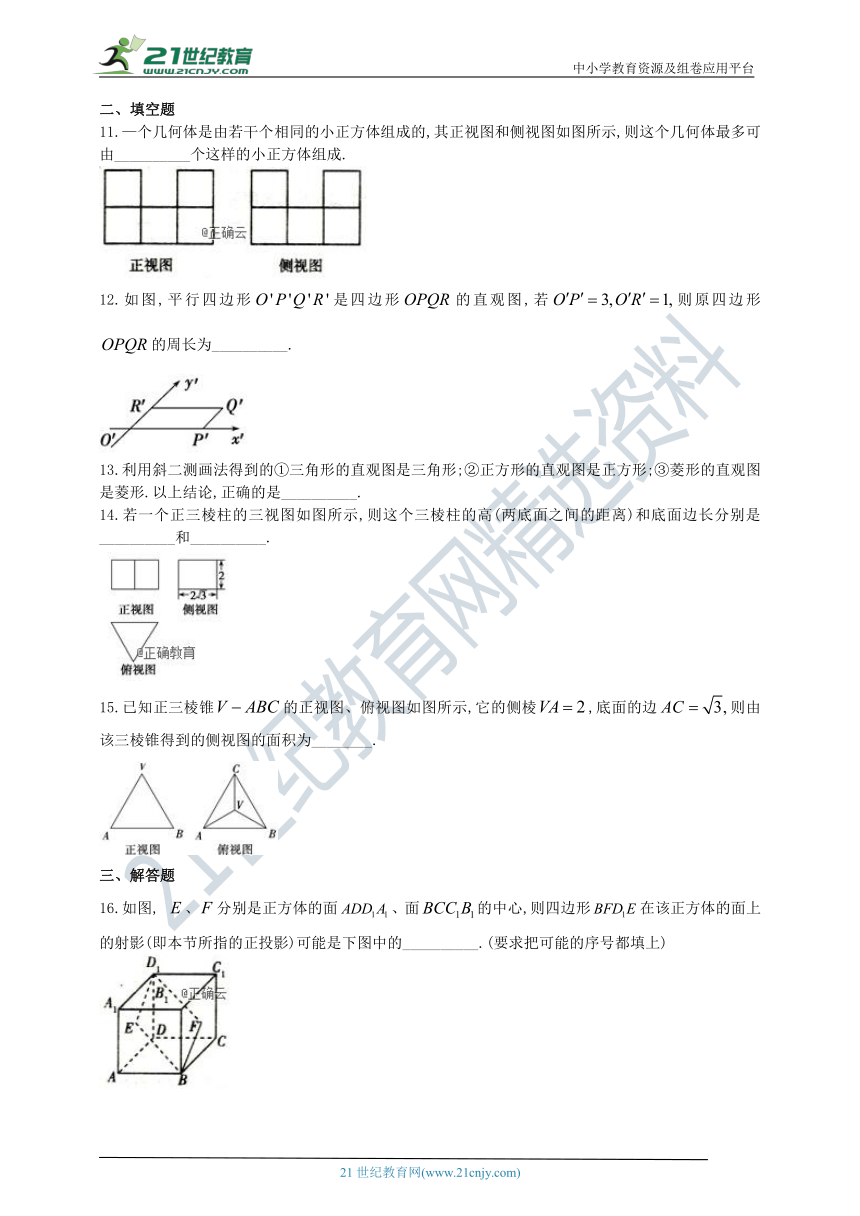
中小学教育资源及组卷应用平台
必修二 第一章空间几何体 1.2空间几何体的三视图与直观图专题训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.若某几何体的三视图如图所示,则这个几何体的直观图可以是(?? )
A. B. C. D.
2.如图所示为一个简单几何体的三视图,则其对应的实物图是(???)
A. B. C. D.
3.已知一几何体的三视图,则它的体积为( )
A. B. C.1 D.2
4.下列说法正确的是(?? )
A.任何物体的三视图都与观察者的观察角度有关
B.任何物体的三视图都与观察者的观察角度无关
C.有的物体的三视图与观察者的观察角度无关
D.正方体的三视图一定是三个全等的正方形
5.如图,矩形是水平放置的一个平面图形的直观图,其中则原图形是(???)
A.正方形?????B.矩形???????C.菱形???????D.梯形
6.水平放置的有一边在水平线上,它的斜二测直观图是正,则为(???)
A.锐角三角形????????????????????????B.直角三角形
C.钝角三角形????????????????????????D.以上都有可能
7.若一个三角形采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的(???)
A. 倍
B. 倍
C. 倍
D. 倍
8.一个棱锥的三视图如图,则该棱锥的全面积(单位: )为(???)
A.
B.
C.
D.
9.某几何体的三视图如图所示,则改几何体的体积为(???)
A.
B.
C.
D.
10.一个几何体的三视图及其尺寸(单位:cm)如图所示,则该几何体的表面积为(?? )cm2
A.64?????????B.80?????????C.112????????D.144
二、填空题
11.—个几何体是由若干个相同的小正方体组成的,其正视图和侧视图如图所示,则这个几何体最多可由__________个这样的小正方体组成.
12.如图,平行四边形是四边形的直观图,若则原四边形的周长为__________.
13.利用斜二测画法得到的①三角形的直观图是三角形;②正方形的直观图是正方形;③菱形的直观图是菱形.以上结论,正确的是__________.
14.若一个正三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是__________和__________.
15.已知正三棱锥的正视图、俯视图如图所示,它的侧棱,底面的边则由该三棱锥得到的侧视图的面积为________.
三、解答题
16.如图, 、分别是正方体的面、面的中心,则四边形在该正方体的面上的射影(即本节所指的正投影)可能是下图中的__________.(要求把可能的序号都填上)
17.如图所示的是某两个几何体的三视图,试判断这两个几何体的形状.
参考答案
1.答案:D
解析:的正视图不符合要求, 的俯视图不符合要求
2.答案:A
解析:
3.答案:C
解析:
4.答案:C
解析:球的三视图与观察者的观察角度无关.而棱柱或棱锥的三视图与观察者的观察角度有关,对于正方体,观察者的观察角度不同,它的三视图也不同.
5.答案:C
解析:设轴与交于点,则.在原图形中, 且
所以,所以原图形是菱形.
6.答案:C
解析:如下图所示,斜二测直观图还原为平面图形,故是钝角三角形.
7.答案:A
解析:
8.答案:A
解析:
9.答案:C
解析:
10.答案:D
解析:
11.答案:13
解析:依题意可知,这个几何体最多可由个这样的小正方体组成.
12.答案:10
解析:由四边形的直观图可知原四边形是矩形,且,所以原四边形
的周长为
13.答案:①
解析:
①正确.②错,正方形的直观图是平行四边形;③错,利用斜二测画法画菱形的直观图时,相邻两边不一定再相等,故不一定是菱形.
14.答案:2; 4
解析:正三棱柱的高同侧视图的高,侧视图的宽度恰为底面正三角形的高,故底面边长为4.
15.答案:
解析:
正三棱锥的侧视图不是一个等腰三角形,而是一个以一条侧棱、该侧棱所对面的斜高和底面正三角形的一条高构成的三角形,如侧视图所示(其中是斜高),由所给数据知原几何体的高为,且
故侧视图的面积为
16.答案:②③
解析:先考虑在面上的投影: 的投影仍然是的投影是的中点,
的投影是的中点, 的投影是.
因此,投影就是题图②.
同理,苛求得在面上的投影也是题图②,
而在面上的投影是一条线段,即题图③.
故应填②③.
17.答案:
①由俯视图知该几何体为多面体,结合正视图和侧视图知,几何体应为正六棱锥.
②由几何体的三视图知该几何体的底面是圆,相交的一部分是一个与底面同圆心的圆,正视图和侧视图是由两个全等的等腰梯形组成的.
故该几何体是两个圆台的组合体.
解析:
_21?????????è?????(www.21cnjy.com)_
必修二 第一章空间几何体 1.2空间几何体的三视图与直观图专题训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.若某几何体的三视图如图所示,则这个几何体的直观图可以是(?? )
A. B. C. D.
2.如图所示为一个简单几何体的三视图,则其对应的实物图是(???)
A. B. C. D.
3.已知一几何体的三视图,则它的体积为( )
A. B. C.1 D.2
4.下列说法正确的是(?? )
A.任何物体的三视图都与观察者的观察角度有关
B.任何物体的三视图都与观察者的观察角度无关
C.有的物体的三视图与观察者的观察角度无关
D.正方体的三视图一定是三个全等的正方形
5.如图,矩形是水平放置的一个平面图形的直观图,其中则原图形是(???)
A.正方形?????B.矩形???????C.菱形???????D.梯形
6.水平放置的有一边在水平线上,它的斜二测直观图是正,则为(???)
A.锐角三角形????????????????????????B.直角三角形
C.钝角三角形????????????????????????D.以上都有可能
7.若一个三角形采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的(???)
A. 倍
B. 倍
C. 倍
D. 倍
8.一个棱锥的三视图如图,则该棱锥的全面积(单位: )为(???)
A.
B.
C.
D.
9.某几何体的三视图如图所示,则改几何体的体积为(???)
A.
B.
C.
D.
10.一个几何体的三视图及其尺寸(单位:cm)如图所示,则该几何体的表面积为(?? )cm2
A.64?????????B.80?????????C.112????????D.144
二、填空题
11.—个几何体是由若干个相同的小正方体组成的,其正视图和侧视图如图所示,则这个几何体最多可由__________个这样的小正方体组成.
12.如图,平行四边形是四边形的直观图,若则原四边形的周长为__________.
13.利用斜二测画法得到的①三角形的直观图是三角形;②正方形的直观图是正方形;③菱形的直观图是菱形.以上结论,正确的是__________.
14.若一个正三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是__________和__________.
15.已知正三棱锥的正视图、俯视图如图所示,它的侧棱,底面的边则由该三棱锥得到的侧视图的面积为________.
三、解答题
16.如图, 、分别是正方体的面、面的中心,则四边形在该正方体的面上的射影(即本节所指的正投影)可能是下图中的__________.(要求把可能的序号都填上)
17.如图所示的是某两个几何体的三视图,试判断这两个几何体的形状.
参考答案
1.答案:D
解析:的正视图不符合要求, 的俯视图不符合要求
2.答案:A
解析:
3.答案:C
解析:
4.答案:C
解析:球的三视图与观察者的观察角度无关.而棱柱或棱锥的三视图与观察者的观察角度有关,对于正方体,观察者的观察角度不同,它的三视图也不同.
5.答案:C
解析:设轴与交于点,则.在原图形中, 且
所以,所以原图形是菱形.
6.答案:C
解析:如下图所示,斜二测直观图还原为平面图形,故是钝角三角形.
7.答案:A
解析:
8.答案:A
解析:
9.答案:C
解析:
10.答案:D
解析:
11.答案:13
解析:依题意可知,这个几何体最多可由个这样的小正方体组成.
12.答案:10
解析:由四边形的直观图可知原四边形是矩形,且,所以原四边形
的周长为
13.答案:①
解析:
①正确.②错,正方形的直观图是平行四边形;③错,利用斜二测画法画菱形的直观图时,相邻两边不一定再相等,故不一定是菱形.
14.答案:2; 4
解析:正三棱柱的高同侧视图的高,侧视图的宽度恰为底面正三角形的高,故底面边长为4.
15.答案:
解析:
正三棱锥的侧视图不是一个等腰三角形,而是一个以一条侧棱、该侧棱所对面的斜高和底面正三角形的一条高构成的三角形,如侧视图所示(其中是斜高),由所给数据知原几何体的高为,且
故侧视图的面积为
16.答案:②③
解析:先考虑在面上的投影: 的投影仍然是的投影是的中点,
的投影是的中点, 的投影是.
因此,投影就是题图②.
同理,苛求得在面上的投影也是题图②,
而在面上的投影是一条线段,即题图③.
故应填②③.
17.答案:
①由俯视图知该几何体为多面体,结合正视图和侧视图知,几何体应为正六棱锥.
②由几何体的三视图知该几何体的底面是圆,相交的一部分是一个与底面同圆心的圆,正视图和侧视图是由两个全等的等腰梯形组成的.
故该几何体是两个圆台的组合体.
解析:
_21?????????è?????(www.21cnjy.com)_
