人教版 九年级下册数学 28.1 锐角三角函数 专题训练 (Word版 含解析)
文档属性
| 名称 | 人教版 九年级下册数学 28.1 锐角三角函数 专题训练 (Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 21:37:55 | ||
图片预览




文档简介
人教版数学九年级下册28.1--锐角三角函数
专题训练
一、选择题
在中,,,,则sin
A的值是?
???
A.
B.
C.
D.
在中,,,则sin
A的值为?
???
A.
B.
C.
D.
在中,若,则一定是?
???
A.
锐角三角形
B.
钝角三角形
C.
等边三角形
D.
等腰直角三角形
如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为?
?
A.
B.
C.
D.
若,且,则为?
???
A.
B.
C.
D.
如图,为了方便行人推车过某天桥,市政府在高的天桥一侧修建了长的斜道.我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是
A.
B.
C.
D.
如果,那么锐角的取值范围是?
???
A.
B.
C.
D.
如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的正切值?
???
A.
扩大为原来的两倍
B.
缩小为原来的
C.
不变
D.
无法确定
如图,在中,,,,于D,则的值为?
???
A.
B.
C.
D.
若为锐角,且,则?
???
A.
B.
C.
D.
如图,点,,在上,BD是的一条弦,则sin
B的值为?
???
A.
B.
C.
D.
计算:
A.
B.
2
C.
D.
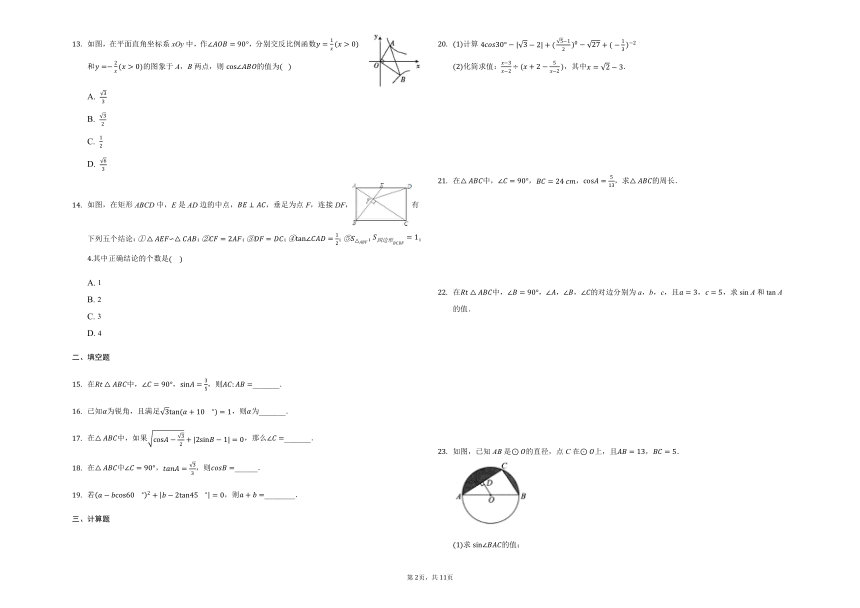
如图,在平面直角坐标系xOy中,作,分别交反比例函数和的图象于A,B两点,则的值为?
A.
B.
C.
D.
如图,在矩形ABCD中,E是AD边的中点,,垂足为点F,连接DF,有下列五个结论:∽;;;;::其中正确结论的个数是
A.
1
B.
2
C.
3
D.
4
二、填空题
在中,,,则_______.
已知为锐角,且满足,则为_______.
在中,如果,那么_______.
在中,,则______.
若,则________.
三、计算题
计算
化简求值:,其中.
在中,,,,求的周长.
在中,,,,的对边分别为a,b,c,且,,求sin
A和tan
A的值.
如图,已知AB是的直径,点C在上,且,.
求的值;
若,垂足为点D,求AD的长;
求图中阴影部分的面积精确到,取
如图,抛物线交x轴于、B两点,交y轴于点,点D是线段BC下方的抛物线上一个动点,过点D作轴于点E,交线段BC于点F.
求抛物线的表达式;
求面积的最大值,并写出此时点D的坐标.
是否存在点D,使得与相似,若存在,求出点D的坐标,若不存在,请说明理由.
如图,在中,D为BC上一定点,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于F,交AE于点M,EF为的平分线,且.
求证:AD为的平分线;
若,求的正弦值;
在问的条件下,如果,求的面积.
答案和解析
1.【答案】D
【解析】
【分析】
本题考查了正弦的定义:在直角三角形中,一锐角的正弦等于这个角的对边与斜边的比值.先利用勾股定理求得,再根据正弦的定义得到,然后把,代入即可得到sinA的值.
【解答】
解:如图,
,,,
.
故选D.
2.【答案】D
【解析】
【分析】
本题主要考查了三角形内角和定理及特殊角的三角函数值,比较简单.根据三角形内角和定理得出,然后根据特殊角的三角函数值即可得出答案.
【解答】
解:在中,,,
根据三角形内角和定理,
,,
.
故选D.
3.【答案】D
【解析】
【分析】
本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.
根据非负数的和为零,可得每个非负数同时为零,根据特殊角三角函数值,可得A、B的值,根据直角三角形的判定,可得答案.
【解答】
解:由,,得
,.
解得,,
则一定是等腰直角三角形,
故选D.
4.【答案】D
【解析】解:如图,过C作于D,则,
.
.
故选:D.
过C作于D,首先根据勾股定理求出AC,然后在中即可求出的值.
本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.
5.【答案】A
【解析】
【分析】
本题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
直接利用特殊角的三角函数值得出答案.
【解答】
解:,
,
,
,
.
故选A.
6.【答案】A
【解析】
【分析】
本题考查了计算器三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键,先利用正弦的定义得到,然后利用计算器求锐角.
【解答】
解:,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为.
故选A.
7.【答案】A
【解析】
【分析】
本题考查了锐角三角函数的增减性和特殊角的三角函数值,利用了锐角函数的正弦值随锐角的增大而增大.熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键首先明确,再根据正弦函数随角增大而增大,进行分析.
【解答】
解:,正弦函数随角的增大而增大,
,
.
故选A.
8.【答案】C
【解析】
【分析】
本题考查了锐角三角函数的定义,掌握在直角三角形中,一个锐角的余弦等于它的邻边与斜边的比值是解题的关键.根据三边的长度都扩大为原来的两倍所得的三角形与原三角形相似,得到锐角A的大小没改变,从而得出答案.
【解答】
解:因为三边的长度都扩大为原来的两倍所得的三角形与原三角形相似,
所以锐角A的大小没改变,所以锐角A的余弦值也不变.
故选C.
9.【答案】D
【解析】
【分析】
本题考查的是解直角三角形,掌握正切的定义是解题的关键.根据勾股定理得到BC,根据同角的余角相等得到,根据正切的定义计算即可.
【解答】
解:,
,
,
,
,
,
故选D.
10.【答案】C
【解析】
【分析】
本题主要考查特殊角的三角函数值,比较简单.
根据特殊角的三角函数值即可解答.
【解答】
解:为锐角,,
,
.
故选C.
11.【答案】D
【解析】
【分析】
本题主要考查圆周角定理,勾股定理,连接CD,根据圆周角定理可得CD为的直径,结合勾股定理可求解CD的长,再利用锐角三角形函数定义可求解.
【解答】
解:连结CD,
,,
,,
,
为的直径,且,
,
.
故选D.
12.【答案】C
【解析】解:
故选:C.
根据实数的运算,即可解答.
本题考查了实数的运算,解决本题的关键是熟记实数的运算.
13.【答案】D
【解析】
【试题解析】
【分析】
本题考查了反比例函数的性质、勾股定理、三角形相似的判定与性质以及锐角三角函数的定义,熟练掌握反比例函数的性质、勾股定理、三角形相似的判定与性质以及锐角三角函数的定义是解题关键设,,证明,得到,即,再用含有a、b的式子表示出,,即可求出,即可得到的值.
【解答】
解:如图所示,过A作y轴垂线,垂足为C,过B作y轴垂线,垂足为D,
反比例函数,,
设,,
,,,,
,
,
,
,
,
,
,即,
在直角三角形AOC和BDO中,?
,,
,
,
设,则,
在直角三角形AOB中,
,
.
故选D.
14.【答案】D
【解析】
【分析】
本题主要考查了相似三角形的判定和性质,矩形的性质,图形面积的计算以及锐角三角函数定义的综合应用,正确的作出辅助线构造平行四边形是解题的关键.解题时注意:相似三角形的对应边成比例.
四边形ABCD是矩形,,则,又,于是∽;故正确;
由,又,所以;故正确;
过D作交AC于N,得到四边形BMDE是平行四边形,求出,得到,根据线段的垂直平分线的性质可得结论,故正确;
设,,则,由∽,得出,进而得出故错误;
由,推出,设,推出,,,,推出::4,故正确;
【解答】
解:如图,过D作交AC于N,
四边形ABCD是矩形,
,,,
于点F,
,,
∽,故正确;
,
∽,
,
,
,
,故正确;
,,
四边形BMDE是平行四边形,
,
,
,
于点F,,
,
垂直平分CF,
,故正确;
设,,则,
四边形ABCD为矩形,
,,
,
∽,
,
,即,
,故错误;
,
,设,
,,,,
::4,故正确;
故选D.
15.【答案】4:5
【解析】
【分析】
本题考查锐角三角函数的定义以及勾股定理的运用,能够根据边和三角函数,求出其他的边根据sinA和勾股定理求出AC的长即可.
【解答】
解:如图,在中,,,
,
设,,
,
:::5.
故答案为4:5.
16.【答案】
【解析】
【分析】
本题主要考查了特殊角的三角函数值的应用,能熟记特殊角的三角函数值是解此题的关键.求出,根据特殊角的三角函数值求出,即可得出答案.
【解答】
解:,
,
,
.
故答案为.
17.【答案】
【解析】
【分析】
本题考查了特殊角的三角函数值、绝对值及二次根式的非负性,熟练记忆一些特殊角的三角函数值是解题关键.根据绝对值及二次根式的非负性,求出cosA、sinB的值,继而得出、的度数,利用内角和定理可求出.
【解答】
解:,
,,
,,
,,
.
故答案为.
18.【答案】
【解析】解:利用三角函数的定义及勾股定理求解.
在中,,,
设,,则,
.
故答案为:.
本题可以利用锐角三角函数的定义求解,也可以利用互为余角的三角函数关系式求解.
此题考查的知识点是特殊角的三角函数值,关键明确求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角或余角的三角函数关系式求三角函数值.
19.【答案】3
【解析】
【分析】
本题主要考查非负数的性质以及特殊角的三角函数值,正确掌握特殊角的三角函数值是解题的关键,先利用非负数的性质和特殊角的三角函数值求出a,b的值,再代入求值即可.
【解答】
解:,
,,
,,
,,
,,
.
故答案为3.
20.【答案】解:
;
,
当时,原式.
【解析】根据特殊角的三角函数值、绝对值、零指数幂和负整数指数幂可以解答本题;
根据分式的加减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
本题考查分式化简求值、特殊角的三角函数值、绝对值、零指数幂和负整数指数幂,解答本题的关键是明确它们各自的计算方法.
21.【答案】解:,
设?cm,则?cm.
在中,.
由,得,
,,
的周长为.
【解析】本题主要考查锐角三角函数的定义和勾股定理,不是很难.
首先根据锐角三角函数的定义设?cm,则?cm,由勾股定理BC,得到x的值,即可求出AB、AC,然后求出周长.
22.【答案】解:在中,,,,
,
,
.
【解析】本题主要考查的是勾股定理,锐角三角函数的定义的有关知识,先利用勾股定理求出b,然后利用锐角三角函数的定义进行求解即可.
23.【答案】解:是直径,
,
;
,OD过O,
;
阴影部分的面积
,
即图中阴影部分的面积约是.
【解析】本题考查了圆的面积,三角形的面积,圆周角定理,垂径定理,勾股定理的应用,主要考查学生运用定理进行推理和计算的能力.
根据圆周角定理求出,解直角三角形即可;
根据勾股定理求出AC,根据垂径定理求出AD即可;
分别求出圆O的面积和三角形ACB的面积,即可得出答案.
24.【答案】解:将点A、C的坐标代入抛物线表达式得,解得,
故抛物线的表达式为;
令,解得或,故点,
由点B、C的坐标得,直线BC的表达式为,
设点,则点,
则面积,
,故面积存在最大值,此时,面积最大值为8,
故点D的坐标为;
存在,理由:
设点,由抛物线的表达式知,点,则,
当为直角时,
与相似,则,
轴,则点C、D关于函数的对称轴对称,
抛物线的对称轴为,则点;
当为直角时,
如下图,过点D作轴于点M,
,,
,
,即,
则,解得舍去或,
故点D的坐标为,
故点D的坐标为或
【解析】【试题解析】
本题考查的是二次函数的综合,一次函数与二次函数二次函数的解析式求法,三角形的面积,锐角三角形函数的定义,二次函数的最大值,分类讨论有关知识.
用待定系数法即可求解;
面积,即可求解;
当为直角时,则,则轴,进而求解;当为直角时,证明,则,即可求解.
25.【答案】证明:
是的直径,
又为的平分线,
垂直平分AD,
,,
是的外角,
,
且,
等量代换
为的平分线;
解:连接DM,
是半圆C的直径,
,
::3,
可设,则,
,
,,
,
,
,
,
,
,
在中,;
解:过A点作于N,
,
,
在和中,
,,
∽,
,
,
,
,
,
,
.
【解析】【试题解析】
本题考查相似三角形的判定,勾股定理等知识点的综合运用.
根据题意得到,,根据DE为直径得到,即可得出;
求的正弦值,即求DM:DE,由已知条件,勾股定理,角的正弦值可以求出;
根据的面积公式求出BC,AN的长是关键,根据题意由三角函数即可求出.
第2页,共2页
第1页,共1页
专题训练
一、选择题
在中,,,,则sin
A的值是?
???
A.
B.
C.
D.
在中,,,则sin
A的值为?
???
A.
B.
C.
D.
在中,若,则一定是?
???
A.
锐角三角形
B.
钝角三角形
C.
等边三角形
D.
等腰直角三角形
如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为?
?
A.
B.
C.
D.
若,且,则为?
???
A.
B.
C.
D.
如图,为了方便行人推车过某天桥,市政府在高的天桥一侧修建了长的斜道.我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是
A.
B.
C.
D.
如果,那么锐角的取值范围是?
???
A.
B.
C.
D.
如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的正切值?
???
A.
扩大为原来的两倍
B.
缩小为原来的
C.
不变
D.
无法确定
如图,在中,,,,于D,则的值为?
???
A.
B.
C.
D.
若为锐角,且,则?
???
A.
B.
C.
D.
如图,点,,在上,BD是的一条弦,则sin
B的值为?
???
A.
B.
C.
D.
计算:
A.
B.
2
C.
D.
如图,在平面直角坐标系xOy中,作,分别交反比例函数和的图象于A,B两点,则的值为?
A.
B.
C.
D.
如图,在矩形ABCD中,E是AD边的中点,,垂足为点F,连接DF,有下列五个结论:∽;;;;::其中正确结论的个数是
A.
1
B.
2
C.
3
D.
4
二、填空题
在中,,,则_______.
已知为锐角,且满足,则为_______.
在中,如果,那么_______.
在中,,则______.
若,则________.
三、计算题
计算
化简求值:,其中.
在中,,,,求的周长.
在中,,,,的对边分别为a,b,c,且,,求sin
A和tan
A的值.
如图,已知AB是的直径,点C在上,且,.
求的值;
若,垂足为点D,求AD的长;
求图中阴影部分的面积精确到,取
如图,抛物线交x轴于、B两点,交y轴于点,点D是线段BC下方的抛物线上一个动点,过点D作轴于点E,交线段BC于点F.
求抛物线的表达式;
求面积的最大值,并写出此时点D的坐标.
是否存在点D,使得与相似,若存在,求出点D的坐标,若不存在,请说明理由.
如图,在中,D为BC上一定点,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于F,交AE于点M,EF为的平分线,且.
求证:AD为的平分线;
若,求的正弦值;
在问的条件下,如果,求的面积.
答案和解析
1.【答案】D
【解析】
【分析】
本题考查了正弦的定义:在直角三角形中,一锐角的正弦等于这个角的对边与斜边的比值.先利用勾股定理求得,再根据正弦的定义得到,然后把,代入即可得到sinA的值.
【解答】
解:如图,
,,,
.
故选D.
2.【答案】D
【解析】
【分析】
本题主要考查了三角形内角和定理及特殊角的三角函数值,比较简单.根据三角形内角和定理得出,然后根据特殊角的三角函数值即可得出答案.
【解答】
解:在中,,,
根据三角形内角和定理,
,,
.
故选D.
3.【答案】D
【解析】
【分析】
本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.
根据非负数的和为零,可得每个非负数同时为零,根据特殊角三角函数值,可得A、B的值,根据直角三角形的判定,可得答案.
【解答】
解:由,,得
,.
解得,,
则一定是等腰直角三角形,
故选D.
4.【答案】D
【解析】解:如图,过C作于D,则,
.
.
故选:D.
过C作于D,首先根据勾股定理求出AC,然后在中即可求出的值.
本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.
5.【答案】A
【解析】
【分析】
本题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
直接利用特殊角的三角函数值得出答案.
【解答】
解:,
,
,
,
.
故选A.
6.【答案】A
【解析】
【分析】
本题考查了计算器三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键,先利用正弦的定义得到,然后利用计算器求锐角.
【解答】
解:,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为.
故选A.
7.【答案】A
【解析】
【分析】
本题考查了锐角三角函数的增减性和特殊角的三角函数值,利用了锐角函数的正弦值随锐角的增大而增大.熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键首先明确,再根据正弦函数随角增大而增大,进行分析.
【解答】
解:,正弦函数随角的增大而增大,
,
.
故选A.
8.【答案】C
【解析】
【分析】
本题考查了锐角三角函数的定义,掌握在直角三角形中,一个锐角的余弦等于它的邻边与斜边的比值是解题的关键.根据三边的长度都扩大为原来的两倍所得的三角形与原三角形相似,得到锐角A的大小没改变,从而得出答案.
【解答】
解:因为三边的长度都扩大为原来的两倍所得的三角形与原三角形相似,
所以锐角A的大小没改变,所以锐角A的余弦值也不变.
故选C.
9.【答案】D
【解析】
【分析】
本题考查的是解直角三角形,掌握正切的定义是解题的关键.根据勾股定理得到BC,根据同角的余角相等得到,根据正切的定义计算即可.
【解答】
解:,
,
,
,
,
,
故选D.
10.【答案】C
【解析】
【分析】
本题主要考查特殊角的三角函数值,比较简单.
根据特殊角的三角函数值即可解答.
【解答】
解:为锐角,,
,
.
故选C.
11.【答案】D
【解析】
【分析】
本题主要考查圆周角定理,勾股定理,连接CD,根据圆周角定理可得CD为的直径,结合勾股定理可求解CD的长,再利用锐角三角形函数定义可求解.
【解答】
解:连结CD,
,,
,,
,
为的直径,且,
,
.
故选D.
12.【答案】C
【解析】解:
故选:C.
根据实数的运算,即可解答.
本题考查了实数的运算,解决本题的关键是熟记实数的运算.
13.【答案】D
【解析】
【试题解析】
【分析】
本题考查了反比例函数的性质、勾股定理、三角形相似的判定与性质以及锐角三角函数的定义,熟练掌握反比例函数的性质、勾股定理、三角形相似的判定与性质以及锐角三角函数的定义是解题关键设,,证明,得到,即,再用含有a、b的式子表示出,,即可求出,即可得到的值.
【解答】
解:如图所示,过A作y轴垂线,垂足为C,过B作y轴垂线,垂足为D,
反比例函数,,
设,,
,,,,
,
,
,
,
,
,
,即,
在直角三角形AOC和BDO中,?
,,
,
,
设,则,
在直角三角形AOB中,
,
.
故选D.
14.【答案】D
【解析】
【分析】
本题主要考查了相似三角形的判定和性质,矩形的性质,图形面积的计算以及锐角三角函数定义的综合应用,正确的作出辅助线构造平行四边形是解题的关键.解题时注意:相似三角形的对应边成比例.
四边形ABCD是矩形,,则,又,于是∽;故正确;
由,又,所以;故正确;
过D作交AC于N,得到四边形BMDE是平行四边形,求出,得到,根据线段的垂直平分线的性质可得结论,故正确;
设,,则,由∽,得出,进而得出故错误;
由,推出,设,推出,,,,推出::4,故正确;
【解答】
解:如图,过D作交AC于N,
四边形ABCD是矩形,
,,,
于点F,
,,
∽,故正确;
,
∽,
,
,
,
,故正确;
,,
四边形BMDE是平行四边形,
,
,
,
于点F,,
,
垂直平分CF,
,故正确;
设,,则,
四边形ABCD为矩形,
,,
,
∽,
,
,即,
,故错误;
,
,设,
,,,,
::4,故正确;
故选D.
15.【答案】4:5
【解析】
【分析】
本题考查锐角三角函数的定义以及勾股定理的运用,能够根据边和三角函数,求出其他的边根据sinA和勾股定理求出AC的长即可.
【解答】
解:如图,在中,,,
,
设,,
,
:::5.
故答案为4:5.
16.【答案】
【解析】
【分析】
本题主要考查了特殊角的三角函数值的应用,能熟记特殊角的三角函数值是解此题的关键.求出,根据特殊角的三角函数值求出,即可得出答案.
【解答】
解:,
,
,
.
故答案为.
17.【答案】
【解析】
【分析】
本题考查了特殊角的三角函数值、绝对值及二次根式的非负性,熟练记忆一些特殊角的三角函数值是解题关键.根据绝对值及二次根式的非负性,求出cosA、sinB的值,继而得出、的度数,利用内角和定理可求出.
【解答】
解:,
,,
,,
,,
.
故答案为.
18.【答案】
【解析】解:利用三角函数的定义及勾股定理求解.
在中,,,
设,,则,
.
故答案为:.
本题可以利用锐角三角函数的定义求解,也可以利用互为余角的三角函数关系式求解.
此题考查的知识点是特殊角的三角函数值,关键明确求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角或余角的三角函数关系式求三角函数值.
19.【答案】3
【解析】
【分析】
本题主要考查非负数的性质以及特殊角的三角函数值,正确掌握特殊角的三角函数值是解题的关键,先利用非负数的性质和特殊角的三角函数值求出a,b的值,再代入求值即可.
【解答】
解:,
,,
,,
,,
,,
.
故答案为3.
20.【答案】解:
;
,
当时,原式.
【解析】根据特殊角的三角函数值、绝对值、零指数幂和负整数指数幂可以解答本题;
根据分式的加减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
本题考查分式化简求值、特殊角的三角函数值、绝对值、零指数幂和负整数指数幂,解答本题的关键是明确它们各自的计算方法.
21.【答案】解:,
设?cm,则?cm.
在中,.
由,得,
,,
的周长为.
【解析】本题主要考查锐角三角函数的定义和勾股定理,不是很难.
首先根据锐角三角函数的定义设?cm,则?cm,由勾股定理BC,得到x的值,即可求出AB、AC,然后求出周长.
22.【答案】解:在中,,,,
,
,
.
【解析】本题主要考查的是勾股定理,锐角三角函数的定义的有关知识,先利用勾股定理求出b,然后利用锐角三角函数的定义进行求解即可.
23.【答案】解:是直径,
,
;
,OD过O,
;
阴影部分的面积
,
即图中阴影部分的面积约是.
【解析】本题考查了圆的面积,三角形的面积,圆周角定理,垂径定理,勾股定理的应用,主要考查学生运用定理进行推理和计算的能力.
根据圆周角定理求出,解直角三角形即可;
根据勾股定理求出AC,根据垂径定理求出AD即可;
分别求出圆O的面积和三角形ACB的面积,即可得出答案.
24.【答案】解:将点A、C的坐标代入抛物线表达式得,解得,
故抛物线的表达式为;
令,解得或,故点,
由点B、C的坐标得,直线BC的表达式为,
设点,则点,
则面积,
,故面积存在最大值,此时,面积最大值为8,
故点D的坐标为;
存在,理由:
设点,由抛物线的表达式知,点,则,
当为直角时,
与相似,则,
轴,则点C、D关于函数的对称轴对称,
抛物线的对称轴为,则点;
当为直角时,
如下图,过点D作轴于点M,
,,
,
,即,
则,解得舍去或,
故点D的坐标为,
故点D的坐标为或
【解析】【试题解析】
本题考查的是二次函数的综合,一次函数与二次函数二次函数的解析式求法,三角形的面积,锐角三角形函数的定义,二次函数的最大值,分类讨论有关知识.
用待定系数法即可求解;
面积,即可求解;
当为直角时,则,则轴,进而求解;当为直角时,证明,则,即可求解.
25.【答案】证明:
是的直径,
又为的平分线,
垂直平分AD,
,,
是的外角,
,
且,
等量代换
为的平分线;
解:连接DM,
是半圆C的直径,
,
::3,
可设,则,
,
,,
,
,
,
,
,
,
在中,;
解:过A点作于N,
,
,
在和中,
,,
∽,
,
,
,
,
,
,
.
【解析】【试题解析】
本题考查相似三角形的判定,勾股定理等知识点的综合运用.
根据题意得到,,根据DE为直径得到,即可得出;
求的正弦值,即求DM:DE,由已知条件,勾股定理,角的正弦值可以求出;
根据的面积公式求出BC,AN的长是关键,根据题意由三角函数即可求出.
第2页,共2页
第1页,共1页
