1.2充分条件与必要条件
图片预览








文档简介
(共28张PPT)
知识回顾:
1.四种命题的概念
2.四种命题的关系
一般地,设“若p,则q”为原命题,则:
“若q,则p”为逆命题;
“若﹁ p ,则﹁ q”为否命题;
“若﹁ q ,则﹁ p ”为逆否命题。
同学们,当某一天你和你妈妈在街上遇到老师的时候,你向老师介绍你的妈妈说:“这是我的妈妈”。那么大家想一想这个时候你的妈妈还会不会补充说:“这是我的孩子”呢?
【实例引入】
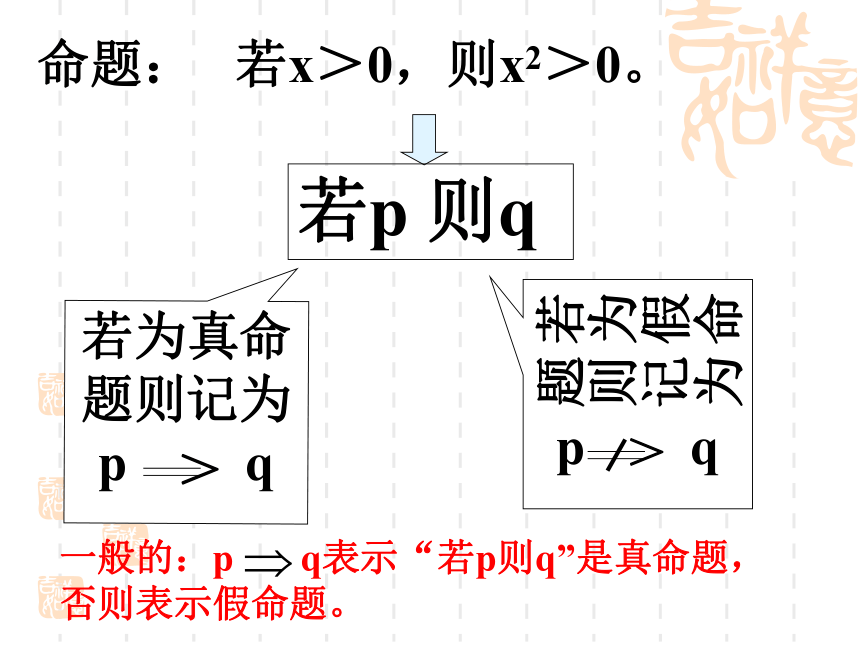
命题: 若x>0,则x2>0。
若p 则q
若为真命题则记为p q
>
若为假命题则记为 p q
>
一般的:p q表示“若p则q”是真命题,否则表示假命题。
例:
真
假
下列命题用推断符号分别怎样表示?
⑴若a>b,则ac>bc;
⑵若a>b,则a+c>b+c;
⑶若x≥0,则x2≥0;
⑷若x>1,则x>0.
(a>b ac>bc)
(a>b a+c>b+c)
(x≥0 x2≥0)
(x>1 x>0)
概念辨析
课本10页 练习 1
充分条件与必要条件:一般地,如果已知 那么就说,p 是q 的充分条件,q 是p 的必要条件.
两三角形全等是两三角形面积相等的充分条件.
两三角形面积相等是两三角形全等的必要条件.
两三角形全等 两三角形面积相等
例如:
例1,下列“若p,则q”形式的命题中,哪些命题 中的p是q的充分条件? (1)若x=1,则x2 –4x+3=0; (2)若f(x)=x,则f(x)为增函数; (3)若x 为无理数,则x2 为无理数
解:命题(1)(2)是真命题,命题(3)是假命题,所以命题(1)(2)中的p是q的充分条件.
【典例演练】
练习1:
(1) 若两个三角形全等,则这两个三角形相似;
(2) 若x > 5,则x > 10。
解:命题(1)是真命题,命题(2)是假命题
所以命题(1)中的p是q的充分条件。
例2 下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1) 若x=y,则x2=y2。
(2) 若两个三角形全等,则这两个三角形的面积相等.
(3) 若a>b,则ac>bc。
解:命题(1)(2)是真命题,命题(3)是假命题,所以命题(1)(2)中的q是p的必要条件。
课本10页 练习 2,3
课本10页 练习 4
能 力 测 试
用符号“充分”或“必要”填空:
(1)“0(2)“四边形的对角线相等”是“这个平行四边形
为正方形”的______条件。
(3)“xy > 0”是“ x+y = x + y ”的______条件。
(4)“个位数是5的整数”是“这个数能被5整除”
的________条件。
充分
必要
充分
充分
请判断下面各组命题中p是否是q的充分条件,p是否是q的必要条件
(1)p:x是6的倍数, q:x是2的倍数
(2) p:x既是2的倍数也是3的倍数, q:x是6的倍数
(3) p:x是4的倍数, q:x是6的倍数
“小范围”是“大范围”的充分条件
从逻辑关系看:
充分非必要条件
必要非充分条件
1)p q且q p,则p是q的
2)若p q且q p,则p是q的
3)若p q且q p,则p是q的
既不充分也不必要条件
充分且必要条件
4)p q且q p,则p是q的
定义:
称:p是q的充分必要条件,简称充要条件
显然,如果p是q的充要条件,那么q也是p的充要条件
p与q互为充要条件
(也可以说成”p与q等价”)
充要条件:同一事物
B
A
1 )
A
B
2 )
A
B
3 )
A = B
4 )
从集合角度看
则称p是q的既不充分也不必要条件
课本12页 练习 1,2
课本12页A组 2,3
例4.已知:圆O的半径r,圆心O到直线L的距离为d,求证:d=r是直线L与圆O相切的充要条件
需分别证明(1)充分性(p q); ? (2)必要性(q p)
证明:
如图,作OP l于点P,则OP=d.
设p:d=r, q:直线L与圆O相切
分析:
l
Q
P
0
┐
d
(1)充分性(p q):
若d=r,则点P在圆O上。在直线l上任取一点Q(异于点P),连接OQ。在RtΔOPQ中, OQ>OP=r。所以,除点P外,直线l 上的点都在圆O的外部。即直线l 与圆O仅有一个公共点P。因此,直线l 与圆O相切。
(2)必要性(q p)
若直线L与圆O相切,不妨设切点为P,则OP L.因此,d=OP=r。
故d=r是直线L与圆O相切的充要条件。
l
Q
P
0
┐
d
l
Q
P
0
┐
d
课本13页B组 2
探究1:若p是q的充分条件,则﹁p是﹁q的什么条件?
﹁p是﹁q的必要条件.
探究2:若p是q的必要条件,则﹁p是﹁q的什么条件?
﹁p是﹁q的充分条件.
新知探究
探究3:若p不是q的充分条件,则q可能是p的必要条件吗?p可能是q的必要条件吗?
新知探究
如果p不是q的充分条件,则q也不是p
的必要条件.
充分条件与必要条件是共存的
若A是B的充要条件,B是C和D的必要条件,E是D的充分条件,E是A的充要条件,
则E是B的_______条件,
C是A的________条件,
A是D的________条件,
D是C的_________条件.
A B
C
D
E
E B
C A
A D
C D
充要条件
充分不必要
充要条件
必要不充分
①r是q的充要条件;
②p是q的充分不必要条件; ③r是q的必要不充分条件;
④┐p是┑s的必要不充分条件;
⑤r是s的充分不必要条件. 则正确命题的序号是( )
A.①④⑤ B.①②④ C.②③⑤ D.②④⑤
用逻辑运算来判断
r
s
q
p
知识回顾:
1.四种命题的概念
2.四种命题的关系
一般地,设“若p,则q”为原命题,则:
“若q,则p”为逆命题;
“若﹁ p ,则﹁ q”为否命题;
“若﹁ q ,则﹁ p ”为逆否命题。
同学们,当某一天你和你妈妈在街上遇到老师的时候,你向老师介绍你的妈妈说:“这是我的妈妈”。那么大家想一想这个时候你的妈妈还会不会补充说:“这是我的孩子”呢?
【实例引入】
命题: 若x>0,则x2>0。
若p 则q
若为真命题则记为p q
>
若为假命题则记为 p q
>
一般的:p q表示“若p则q”是真命题,否则表示假命题。
例:
真
假
下列命题用推断符号分别怎样表示?
⑴若a>b,则ac>bc;
⑵若a>b,则a+c>b+c;
⑶若x≥0,则x2≥0;
⑷若x>1,则x>0.
(a>b ac>bc)
(a>b a+c>b+c)
(x≥0 x2≥0)
(x>1 x>0)
概念辨析
课本10页 练习 1
充分条件与必要条件:一般地,如果已知 那么就说,p 是q 的充分条件,q 是p 的必要条件.
两三角形全等是两三角形面积相等的充分条件.
两三角形面积相等是两三角形全等的必要条件.
两三角形全等 两三角形面积相等
例如:
例1,下列“若p,则q”形式的命题中,哪些命题 中的p是q的充分条件? (1)若x=1,则x2 –4x+3=0; (2)若f(x)=x,则f(x)为增函数; (3)若x 为无理数,则x2 为无理数
解:命题(1)(2)是真命题,命题(3)是假命题,所以命题(1)(2)中的p是q的充分条件.
【典例演练】
练习1:
(1) 若两个三角形全等,则这两个三角形相似;
(2) 若x > 5,则x > 10。
解:命题(1)是真命题,命题(2)是假命题
所以命题(1)中的p是q的充分条件。
例2 下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?
(1) 若x=y,则x2=y2。
(2) 若两个三角形全等,则这两个三角形的面积相等.
(3) 若a>b,则ac>bc。
解:命题(1)(2)是真命题,命题(3)是假命题,所以命题(1)(2)中的q是p的必要条件。
课本10页 练习 2,3
课本10页 练习 4
能 力 测 试
用符号“充分”或“必要”填空:
(1)“0
为正方形”的______条件。
(3)“xy > 0”是“ x+y = x + y ”的______条件。
(4)“个位数是5的整数”是“这个数能被5整除”
的________条件。
充分
必要
充分
充分
请判断下面各组命题中p是否是q的充分条件,p是否是q的必要条件
(1)p:x是6的倍数, q:x是2的倍数
(2) p:x既是2的倍数也是3的倍数, q:x是6的倍数
(3) p:x是4的倍数, q:x是6的倍数
“小范围”是“大范围”的充分条件
从逻辑关系看:
充分非必要条件
必要非充分条件
1)p q且q p,则p是q的
2)若p q且q p,则p是q的
3)若p q且q p,则p是q的
既不充分也不必要条件
充分且必要条件
4)p q且q p,则p是q的
定义:
称:p是q的充分必要条件,简称充要条件
显然,如果p是q的充要条件,那么q也是p的充要条件
p与q互为充要条件
(也可以说成”p与q等价”)
充要条件:同一事物
B
A
1 )
A
B
2 )
A
B
3 )
A = B
4 )
从集合角度看
则称p是q的既不充分也不必要条件
课本12页 练习 1,2
课本12页A组 2,3
例4.已知:圆O的半径r,圆心O到直线L的距离为d,求证:d=r是直线L与圆O相切的充要条件
需分别证明(1)充分性(p q); ? (2)必要性(q p)
证明:
如图,作OP l于点P,则OP=d.
设p:d=r, q:直线L与圆O相切
分析:
l
Q
P
0
┐
d
(1)充分性(p q):
若d=r,则点P在圆O上。在直线l上任取一点Q(异于点P),连接OQ。在RtΔOPQ中, OQ>OP=r。所以,除点P外,直线l 上的点都在圆O的外部。即直线l 与圆O仅有一个公共点P。因此,直线l 与圆O相切。
(2)必要性(q p)
若直线L与圆O相切,不妨设切点为P,则OP L.因此,d=OP=r。
故d=r是直线L与圆O相切的充要条件。
l
Q
P
0
┐
d
l
Q
P
0
┐
d
课本13页B组 2
探究1:若p是q的充分条件,则﹁p是﹁q的什么条件?
﹁p是﹁q的必要条件.
探究2:若p是q的必要条件,则﹁p是﹁q的什么条件?
﹁p是﹁q的充分条件.
新知探究
探究3:若p不是q的充分条件,则q可能是p的必要条件吗?p可能是q的必要条件吗?
新知探究
如果p不是q的充分条件,则q也不是p
的必要条件.
充分条件与必要条件是共存的
若A是B的充要条件,B是C和D的必要条件,E是D的充分条件,E是A的充要条件,
则E是B的_______条件,
C是A的________条件,
A是D的________条件,
D是C的_________条件.
A B
C
D
E
E B
C A
A D
C D
充要条件
充分不必要
充要条件
必要不充分
①r是q的充要条件;
②p是q的充分不必要条件; ③r是q的必要不充分条件;
④┐p是┑s的必要不充分条件;
⑤r是s的充分不必要条件. 则正确命题的序号是( )
A.①④⑤ B.①②④ C.②③⑤ D.②④⑤
用逻辑运算来判断
r
s
q
p
