10.2事件的相互独立性 专题训练(含答案)
文档属性
| 名称 | 10.2事件的相互独立性 专题训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 17:13:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 概率 10.2事件的相互独立性
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.位于直角坐标系原点的质点按以下规则移动:①每次移动一个单位,②向左移动的概率为,向右移动的概率为.移动5次后落点在的概率为( )
A. B.
C. D.
2.在某次人才招聘会上,假定某毕业生赢得甲公司面试机会的概率为,赢得乙、丙两公司面试机会的概率均为,且三个公司是否让其面试是相互独立的.则该毕业生只赢得甲、乙两个公司面试机会的概率为( )
A. B. C. D.
3.甲、乙两人比赛,平手的概率为,乙获胜的概率为,则下列说法正确的是( )
A.甲获胜的概率是 B.甲不输的概率是
C.乙输的概率是 D.乙不输的概率是
4.抛掷一枚均匀的骰子两次,在下列事件中,与事件“第一次得到6点”不互相独立的事件是( )
A.“两次得到的点数和是12” B.“第二次得到6点”
C.“第二次的点数不超过3点” D.“第二次的点数是奇数”
5.在如图所示的电路图中,开关闭合与断开的概率都是,且是相互独立的,则灯灭的概率是 ( )
A. B. C. D.
6.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
A.0.648 B.0.432 C.0.36 D.0.312
7.甲、乙两队进行排球决赛.现在的情形是甲队只要再赢一局就获得冠军,乙队需要再赢两局才能获得冠军.若两队每局获胜的概率相同,则甲队获得冠军的概率为( )
A. B. C. D.
8.端午节放假,甲、乙、丙回老家过节的概率分別为.假定三人的行动相互之间没有影响,那么这段时间内至少有1人回老家过节的概率为( )
A. B. C. D.
9.袋内有3个白球和2个黑球,从中有放回地摸球,如果“第一次摸得白球”记为事件,“第二次摸得白球”记为事件,那么事件与, 与间的关系是( )
A. 与, 与均相互独立 B. 与相互独立, 与互斥
C. 与, 与均互斥 D. 与互斥,与相互独立
10.从一箱产品中随机地抽取一件,设事件{抽到一等品},事件{抽到二等品},事件{抽到三等品},且已知,,,则事件“抽到的产品不是一等品”的概率为(???)
A. B. C. D.
二、填空题
11.甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,则其中恰有一人击中目标的概率是________.
12.设两个独立事件和都不发生的概率为, 发生不发生的概率与发生不发生的概率相同, 则事件发生的概率=__________.
13.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是________.
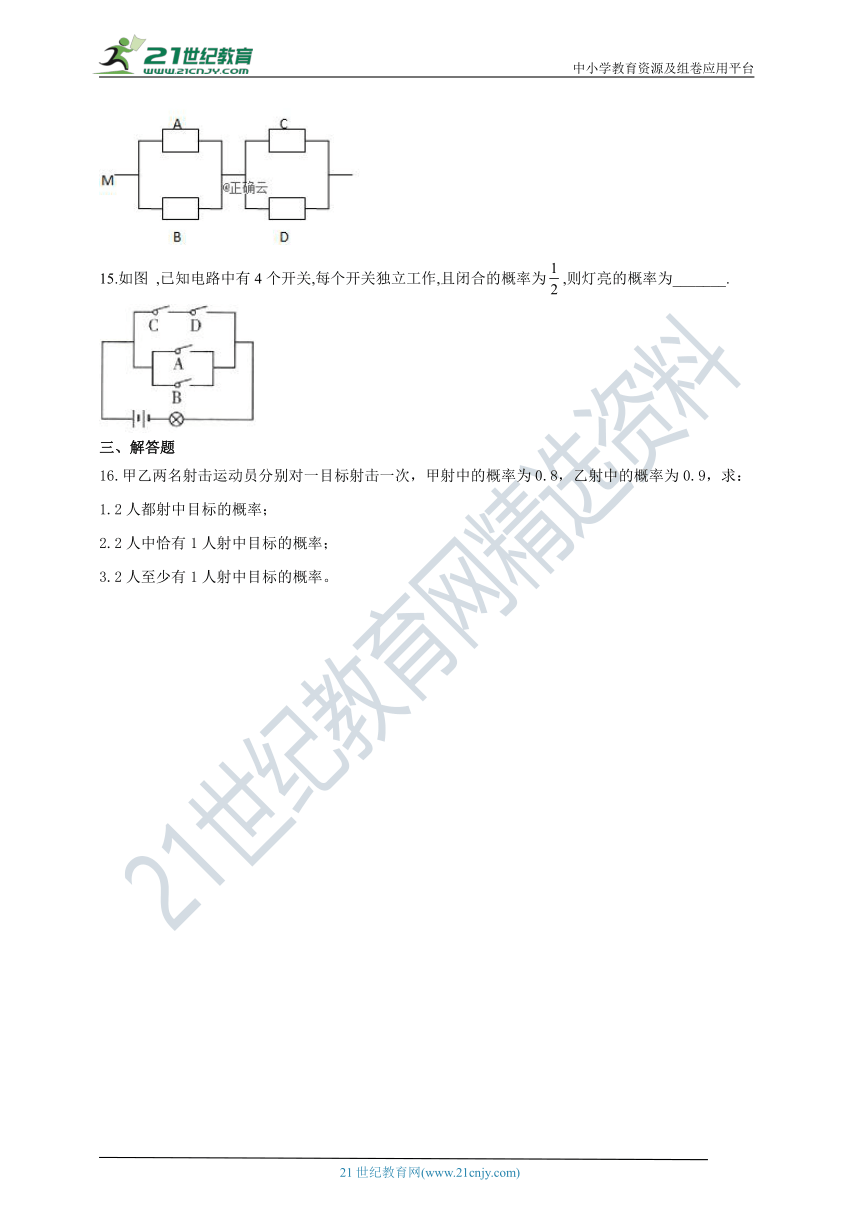
14.如图,系统由四类不同的元件构成.当元件至少有一个正常工作且元件至少有一个正常工作时,系统M正常工作.已知元件正常工作的概率依次为,元件连接成的系统正常工作的概率=__________.
15.如图 ,已知电路中有4个开关,每个开关独立工作,且闭合的概率为,则灯亮的概率为_______.
三、解答题
16.甲乙两名射击运动员分别对一目标射击一次,甲射中的概率为0.8,乙射中的概率为0.9,求:
1.2人都射中目标的概率;
2.2人中恰有1人射中目标的概率;
3.2人至少有1人射中目标的概率。
参考答案
1.答案:A
解析:根据题意,质点移动5次后位于点,其中向左移动了3次,向右移动了2次,其中向左平移的3次有种情况,剩下的2次向右平移,则其概率为,故选A
2.答案:B
解析:记事件A为“该毕业生赢得甲公司的面试机会”,事件B为“该毕业生赢得乙公司的面试机会”,事件C为“该毕业生赢得丙公司的面试机会”.
由题易可得,.
则事件“该毕业生只赢得甲、乙两个公司面试机会”为,
由相互独立事件同时成立的概率公式,可得
.故选B.
3.答案:A
解析:“甲获胜”是“平手或乙获胜”的对立事件,所以“甲获胜”的概率是;设事件A为“甲不输”,则事件A是“甲获胜”和“平手”这两个互斥事件的并事件,所以(或设事件A为“甲不输”,则事件A是“乙获胜”的对立事件,所以);乙输的概率即甲获胜的概率,为;乙不输的概率是.故选A.
4.答案:A
解析:“第二次得到6点”“第二次的点数不超过3点”“第二次的点数是奇数”与事件“第一次得到6点”均相互独立,而对于“两次得到的点数和是12”,则第一次一定是6点,第二次也是6点,故不相互独立,故选A.
5.答案:C
解析:
6.答案:A
解析:根据独立重复试验公式得,该同学通过测试的概率为.
7.答案:D
解析:甲要获得冠军共分为两种情况:
(1)第一场取胜,这种情况的概率为.
(2)第一场失败,第二场取胜,这种情况的概率为,
则甲获得冠军的概率为.
8.答案:B
解析:因为甲、乙、丙回老家过节的概率分别为,所以他们不回老家过节的概率分別为 .“至少有1人回老家过节”的对立事件是“没有人回老家过节”,所以至少有1人回老家过节的概率为.
9.答案:A
解析:因为是有放回地摸球,所以事件的发生不会影响事件的发生,所以事件与, 与均相互独立.
10.答案:C
解析:事件“抽到的产品不是一等品”与事件是对立事件,由于所以由对立事件的概率公式得“抽到的产品不是一等品”的概率为
11.答案:0.48
解析:
12.答案:
解析:由已知,得①,又,所以,即②,由①②,解得,所以
13.答案:0.18
解析:甲队以4:1获胜,甲队在第5场(主场)获胜,前4场中有一场输.
若在主场输一场,则概率为 ;
若在客场输一场,则概率为.
∴甲队以4: 1获胜的概率.
14.答案:0.752
解析:=0.752
15.答案:
解析:记开关闭合为事件,因为开关断开且开关至少有一个断开时,线路才断开,导致灯不亮,所以灯不亮的概率为.所以灯亮的概率为.
16.答案:1.0.72
2.0.26
3.0.98
解析:
_21?????????è?????(www.21cnjy.com)_
第十章 概率 10.2事件的相互独立性
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.位于直角坐标系原点的质点按以下规则移动:①每次移动一个单位,②向左移动的概率为,向右移动的概率为.移动5次后落点在的概率为( )
A. B.
C. D.
2.在某次人才招聘会上,假定某毕业生赢得甲公司面试机会的概率为,赢得乙、丙两公司面试机会的概率均为,且三个公司是否让其面试是相互独立的.则该毕业生只赢得甲、乙两个公司面试机会的概率为( )
A. B. C. D.
3.甲、乙两人比赛,平手的概率为,乙获胜的概率为,则下列说法正确的是( )
A.甲获胜的概率是 B.甲不输的概率是
C.乙输的概率是 D.乙不输的概率是
4.抛掷一枚均匀的骰子两次,在下列事件中,与事件“第一次得到6点”不互相独立的事件是( )
A.“两次得到的点数和是12” B.“第二次得到6点”
C.“第二次的点数不超过3点” D.“第二次的点数是奇数”
5.在如图所示的电路图中,开关闭合与断开的概率都是,且是相互独立的,则灯灭的概率是 ( )
A. B. C. D.
6.投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
A.0.648 B.0.432 C.0.36 D.0.312
7.甲、乙两队进行排球决赛.现在的情形是甲队只要再赢一局就获得冠军,乙队需要再赢两局才能获得冠军.若两队每局获胜的概率相同,则甲队获得冠军的概率为( )
A. B. C. D.
8.端午节放假,甲、乙、丙回老家过节的概率分別为.假定三人的行动相互之间没有影响,那么这段时间内至少有1人回老家过节的概率为( )
A. B. C. D.
9.袋内有3个白球和2个黑球,从中有放回地摸球,如果“第一次摸得白球”记为事件,“第二次摸得白球”记为事件,那么事件与, 与间的关系是( )
A. 与, 与均相互独立 B. 与相互独立, 与互斥
C. 与, 与均互斥 D. 与互斥,与相互独立
10.从一箱产品中随机地抽取一件,设事件{抽到一等品},事件{抽到二等品},事件{抽到三等品},且已知,,,则事件“抽到的产品不是一等品”的概率为(???)
A. B. C. D.
二、填空题
11.甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,则其中恰有一人击中目标的概率是________.
12.设两个独立事件和都不发生的概率为, 发生不发生的概率与发生不发生的概率相同, 则事件发生的概率=__________.
13.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是________.
14.如图,系统由四类不同的元件构成.当元件至少有一个正常工作且元件至少有一个正常工作时,系统M正常工作.已知元件正常工作的概率依次为,元件连接成的系统正常工作的概率=__________.
15.如图 ,已知电路中有4个开关,每个开关独立工作,且闭合的概率为,则灯亮的概率为_______.
三、解答题
16.甲乙两名射击运动员分别对一目标射击一次,甲射中的概率为0.8,乙射中的概率为0.9,求:
1.2人都射中目标的概率;
2.2人中恰有1人射中目标的概率;
3.2人至少有1人射中目标的概率。
参考答案
1.答案:A
解析:根据题意,质点移动5次后位于点,其中向左移动了3次,向右移动了2次,其中向左平移的3次有种情况,剩下的2次向右平移,则其概率为,故选A
2.答案:B
解析:记事件A为“该毕业生赢得甲公司的面试机会”,事件B为“该毕业生赢得乙公司的面试机会”,事件C为“该毕业生赢得丙公司的面试机会”.
由题易可得,.
则事件“该毕业生只赢得甲、乙两个公司面试机会”为,
由相互独立事件同时成立的概率公式,可得
.故选B.
3.答案:A
解析:“甲获胜”是“平手或乙获胜”的对立事件,所以“甲获胜”的概率是;设事件A为“甲不输”,则事件A是“甲获胜”和“平手”这两个互斥事件的并事件,所以(或设事件A为“甲不输”,则事件A是“乙获胜”的对立事件,所以);乙输的概率即甲获胜的概率,为;乙不输的概率是.故选A.
4.答案:A
解析:“第二次得到6点”“第二次的点数不超过3点”“第二次的点数是奇数”与事件“第一次得到6点”均相互独立,而对于“两次得到的点数和是12”,则第一次一定是6点,第二次也是6点,故不相互独立,故选A.
5.答案:C
解析:
6.答案:A
解析:根据独立重复试验公式得,该同学通过测试的概率为.
7.答案:D
解析:甲要获得冠军共分为两种情况:
(1)第一场取胜,这种情况的概率为.
(2)第一场失败,第二场取胜,这种情况的概率为,
则甲获得冠军的概率为.
8.答案:B
解析:因为甲、乙、丙回老家过节的概率分别为,所以他们不回老家过节的概率分別为 .“至少有1人回老家过节”的对立事件是“没有人回老家过节”,所以至少有1人回老家过节的概率为.
9.答案:A
解析:因为是有放回地摸球,所以事件的发生不会影响事件的发生,所以事件与, 与均相互独立.
10.答案:C
解析:事件“抽到的产品不是一等品”与事件是对立事件,由于所以由对立事件的概率公式得“抽到的产品不是一等品”的概率为
11.答案:0.48
解析:
12.答案:
解析:由已知,得①,又,所以,即②,由①②,解得,所以
13.答案:0.18
解析:甲队以4:1获胜,甲队在第5场(主场)获胜,前4场中有一场输.
若在主场输一场,则概率为 ;
若在客场输一场,则概率为.
∴甲队以4: 1获胜的概率.
14.答案:0.752
解析:=0.752
15.答案:
解析:记开关闭合为事件,因为开关断开且开关至少有一个断开时,线路才断开,导致灯不亮,所以灯不亮的概率为.所以灯亮的概率为.
16.答案:1.0.72
2.0.26
3.0.98
解析:
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
