2021年中考数学专题复习课件:解直角三角形(共16张ppt)
文档属性
| 名称 | 2021年中考数学专题复习课件:解直角三角形(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 444.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
解直角三角形2
——中考专题复习
A
B
解直角
三角形
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
温故而知新
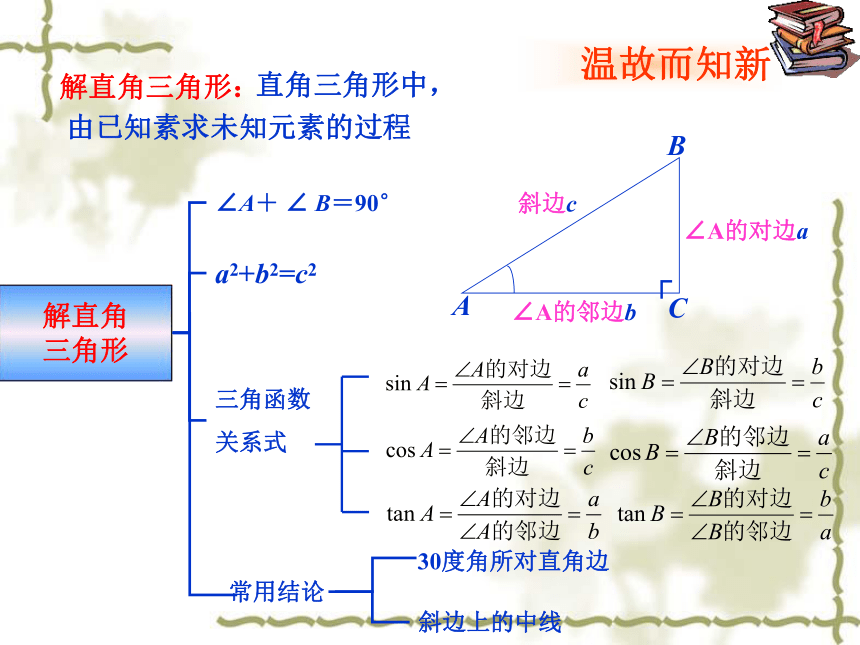
解直角三角形:
由已知素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
常用结论
30度角所对直角边
斜边上的中线
温故而知新
A
B
a
C
b
┌
c
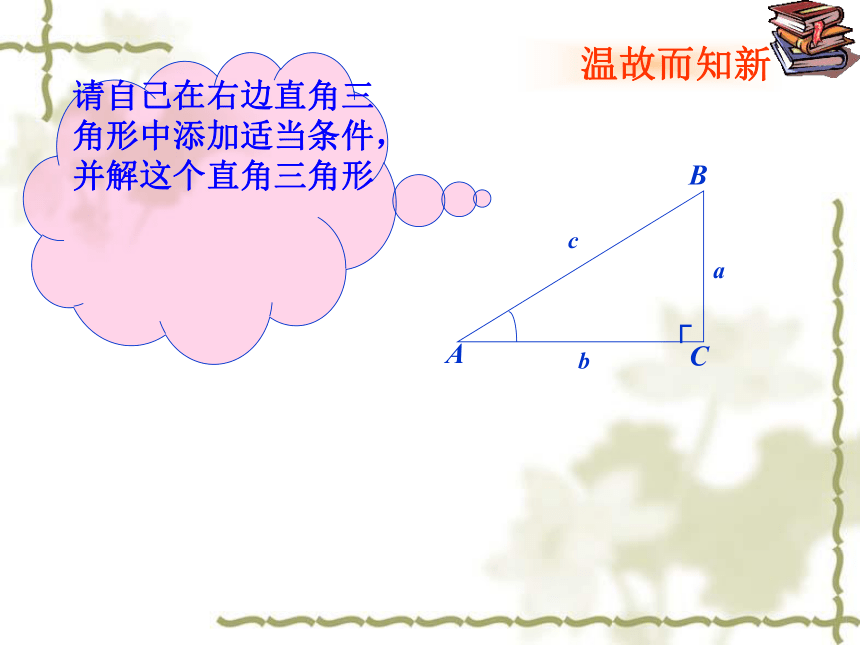
请自己在右边直角三角形中添加适当条件,并解这个直角三角形
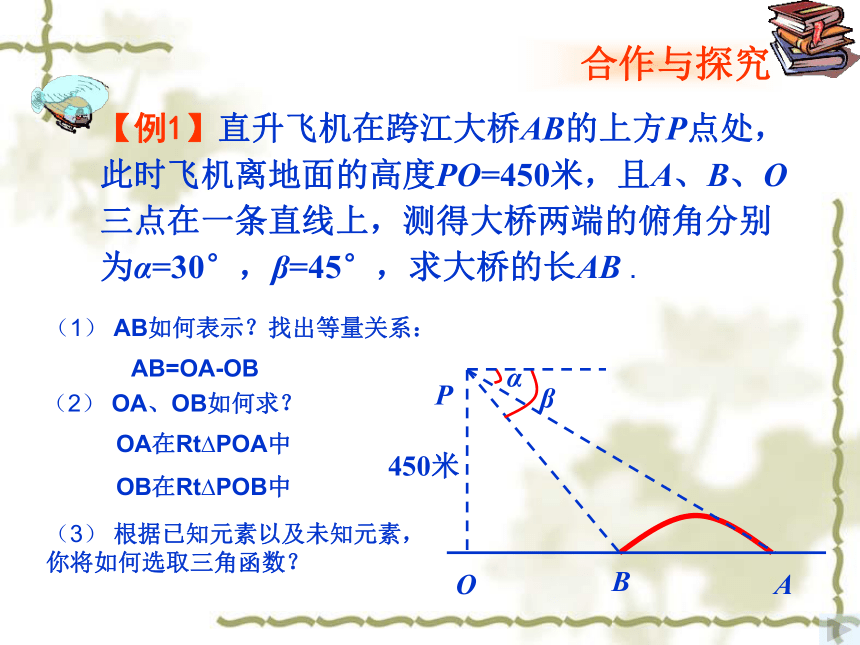
【例1】直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB
.
β
α
P
A
B
O
450米
合作与探究
(1)
AB如何表示?找出等量关系:
AB=OA-OB
(2)
OA、OB如何求?
OA在Rt?POA中
OB在Rt?POB中
(3)
根据已知元素以及未知元素,你将如何选取三角函数?
P
A
B
O
30°
45°
400米
合作与探究
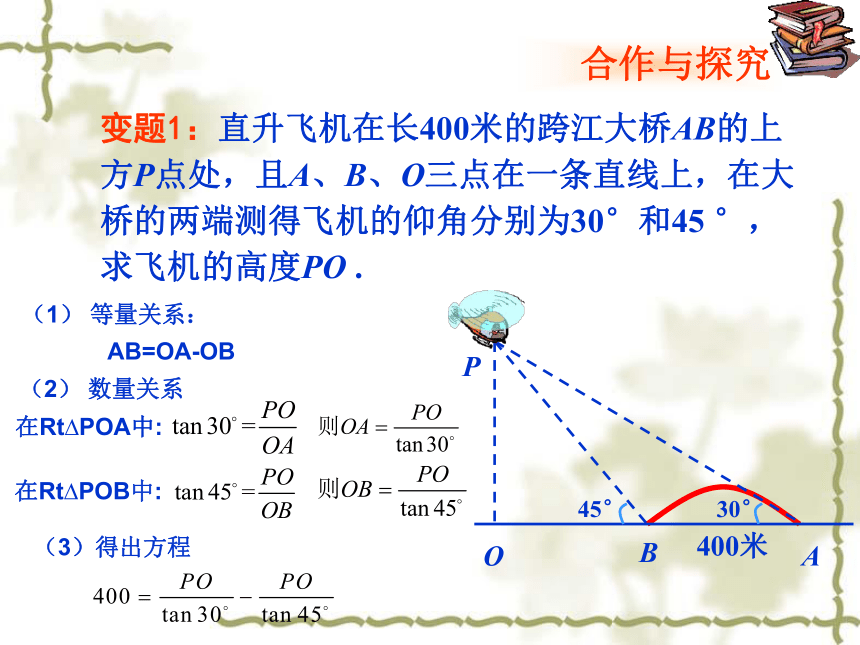
变题1:直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45
°,求飞机的高度PO
.
(1)
等量关系:
AB=OA-OB
(2)
数量关系
在Rt?POA中:
(3)得出方程
在Rt?POB中:
45°
30°
P
O
B
A
200米
C
合作与探究
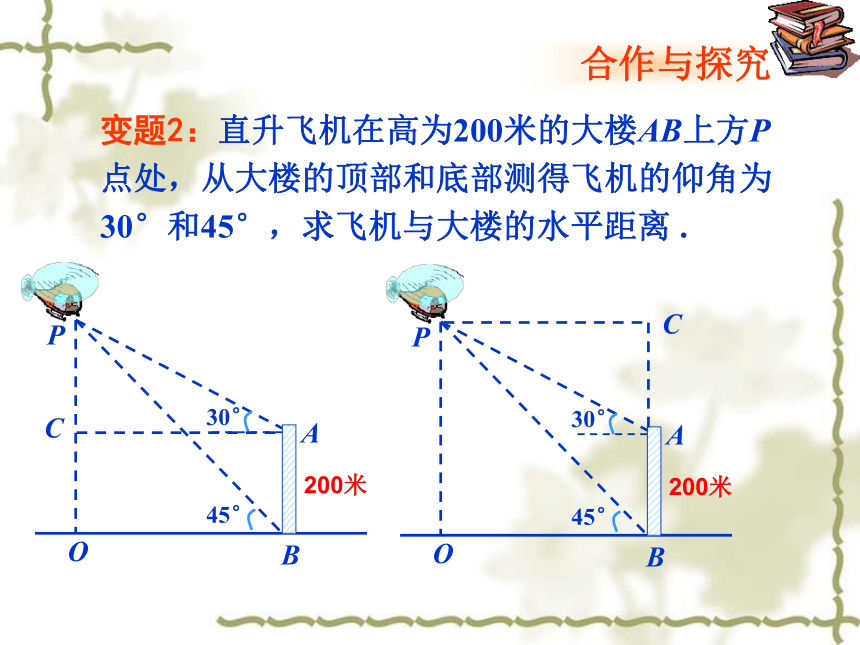
变题2:直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机与大楼的水平距离
.
45°
30°
P
O
B
A
200米
C
45°
30°
200米
P
O
B
A
D
合作与探究
变题3:直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离.
β
α
A
B
O
45°
30°
200米
P
O
B
D
归纳与提高
45°
30°
P
A
200米
C
B
O
β
α
A
B
O
45°
30°
450
45°
30°
400
60°
45°
200
200
45°
30°
走进中考
1、在数学活动课中,小敏为了测量旗杆AB的高度,站在教学楼上的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD为9
m,则旗杆的高度是多少?(结果保留根号)
2.如图所示,A,B两城市相距100km,现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆点,50km为半径的圆形区域内,请问计划修筑的这条高速公路会不会穿越保护区,为什么?
(参考数据:
≈1.732,
≈1.414)
现实对象
数学模型
实际问题的解
数学问题的解
抽象
逻辑推理
翻译回去
2.两类模型
回味无穷
3.一个思路
1.;三种思想
分类,方程,化归
4.
常见模型
(1)“背靠背”型
这种类型的特点是:两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共直角边是沟通两直角三角形关系的媒介。
如图1.
(2)“母抱子”型
这种类型的特点是,一个直角三角形包含在另一个直角三
角形中,两直角三角形有公共直角和一条公共直角边,其
中,这条公共直角边是沟通两直角三角形关系的媒介,
如图4.
(3)“拥抱”型
这种类型的特点是:两直角三角形以交叉方式出现。
如图7.
(4)“斜截”型
这种类型的特点是,在一个直角三角形内,用垂直于斜边的
一条直线去截这个直角三角形,
如图9.新直角三角形与原直角三角形有一个公共锐角,所
剩四边形的对角互补.
解直角三角形2
——中考专题复习
A
B
解直角
三角形
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
温故而知新
解直角三角形:
由已知素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
常用结论
30度角所对直角边
斜边上的中线
温故而知新
A
B
a
C
b
┌
c
请自己在右边直角三角形中添加适当条件,并解这个直角三角形
【例1】直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB
.
β
α
P
A
B
O
450米
合作与探究
(1)
AB如何表示?找出等量关系:
AB=OA-OB
(2)
OA、OB如何求?
OA在Rt?POA中
OB在Rt?POB中
(3)
根据已知元素以及未知元素,你将如何选取三角函数?
P
A
B
O
30°
45°
400米
合作与探究
变题1:直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45
°,求飞机的高度PO
.
(1)
等量关系:
AB=OA-OB
(2)
数量关系
在Rt?POA中:
(3)得出方程
在Rt?POB中:
45°
30°
P
O
B
A
200米
C
合作与探究
变题2:直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机与大楼的水平距离
.
45°
30°
P
O
B
A
200米
C
45°
30°
200米
P
O
B
A
D
合作与探究
变题3:直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离.
β
α
A
B
O
45°
30°
200米
P
O
B
D
归纳与提高
45°
30°
P
A
200米
C
B
O
β
α
A
B
O
45°
30°
450
45°
30°
400
60°
45°
200
200
45°
30°
走进中考
1、在数学活动课中,小敏为了测量旗杆AB的高度,站在教学楼上的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD为9
m,则旗杆的高度是多少?(结果保留根号)
2.如图所示,A,B两城市相距100km,现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆点,50km为半径的圆形区域内,请问计划修筑的这条高速公路会不会穿越保护区,为什么?
(参考数据:
≈1.732,
≈1.414)
现实对象
数学模型
实际问题的解
数学问题的解
抽象
逻辑推理
翻译回去
2.两类模型
回味无穷
3.一个思路
1.;三种思想
分类,方程,化归
4.
常见模型
(1)“背靠背”型
这种类型的特点是:两直角三角形是并列关系,有公共直角顶点和一条公共直角边,其中,这条公共直角边是沟通两直角三角形关系的媒介。
如图1.
(2)“母抱子”型
这种类型的特点是,一个直角三角形包含在另一个直角三
角形中,两直角三角形有公共直角和一条公共直角边,其
中,这条公共直角边是沟通两直角三角形关系的媒介,
如图4.
(3)“拥抱”型
这种类型的特点是:两直角三角形以交叉方式出现。
如图7.
(4)“斜截”型
这种类型的特点是,在一个直角三角形内,用垂直于斜边的
一条直线去截这个直角三角形,
如图9.新直角三角形与原直角三角形有一个公共锐角,所
剩四边形的对角互补.
同课章节目录
