鲁教版七年级上册 6.5:一次函数的应用 练习(Word版 含解析)
文档属性
| 名称 | 鲁教版七年级上册 6.5:一次函数的应用 练习(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 154.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:37:27 | ||
图片预览



文档简介
一次函数的应用练习
一、选择题
A,B两地相距20km,甲乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程与行进时间之间的关系,有下列说法:
甲始终是匀速行进,乙的行进不是匀速的;
乙用了4个小时到达目的地;
乙比甲先出发1小时;
甲在出发4小时后被乙追上.
在这些说法中,正确的有
A.
1个
B.
2个
C.
3个
D.
4个
若一次函数为常数且的图象经过点,则关于x的方程的解为
A.
B.
C.
D.
如图,表示一艘轮船和一艘快艇沿相同路线从甲港岀发到乙港行驶路程随时间变化的图象.则下列结论错误的是
A.
轮船的速度为20千米时
B.
快艇的速度为40千米时
C.
轮船比快艇先出发2小时
D.
快艇到达乙港用了6小时
某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是
A.
310元
B.
300元
C.
290元
D.
280元
已知直线经过点和点,那么关于x的方程的解是
A.
B.
C.
D.
速度分别为和的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离与行驶时间之间的函数关系如图所示.下列说法:;;;若,则其中说法正确的是?
?
A.
B.
C.
D.
数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点P,根据图象可知,方程的解是???????????????????????????????
?????
?
A.
B.
C.
D.
如图,一次函数与x轴的交点为P,则关于x的方程的解为
A.
B.
2
C.
3
D.
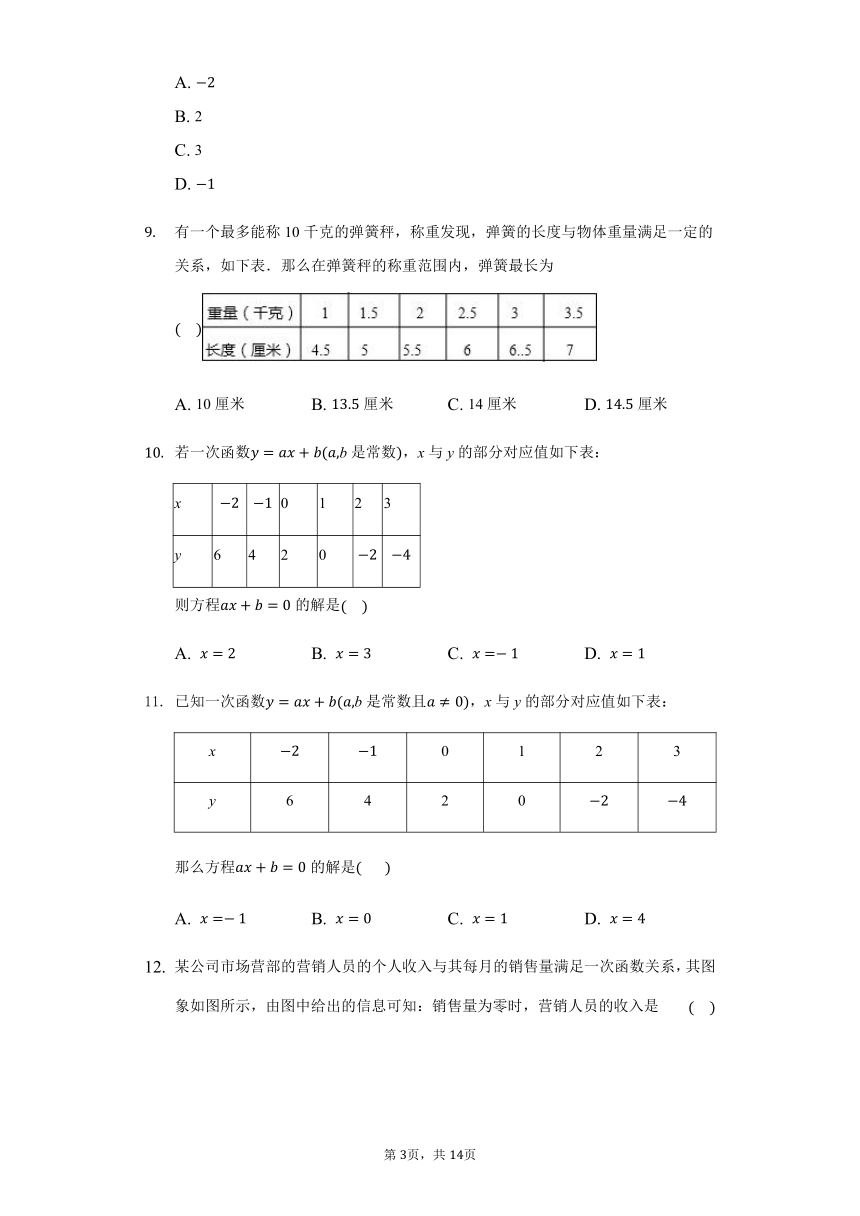
有一个最多能称10千克的弹簧秤,称重发现,弹簧的长度与物体重量满足一定的关系,如下表.那么在弹簧秤的称重范围内,弹簧最长为
A.
10厘米
B.
厘米
C.
14厘米
D.
厘米
若一次函数b是常数,x与y的部分对应值如下表:
x
0
1
2
3
y
6
4
2
0
则方程的解是
A.
B.
C.
D.
已知一次函数b是常数且,x与y的部分对应值如下表:
x
0
1
2
3
y
6
4
2
0
那么方程的解是?
?
A.
B.
C.
D.
某公司市场营部的营销人员的个人收入与其每月的销售量满足一次函数关系,其图象如图所示,由图中给出的信息可知:销售量为零时,营销人员的收入是
A.
280元
B.
290元
C.
300元
D.
310元
甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是
A.
甲车的平均速度为
B.
乙车的平均速度为
C.
乙车比甲车先到B城
D.
乙车比甲车先出发1h
二、填空题
若一次函数的图象如图所示,点在函数图象上,则关于x的方程的解是______.
李明同学的家与学校的距离为2000米,如果他上学步行的速度为y米分,从家里到学校的时间为x分钟,则y与x之间的函数关系式为__________.
已知一次函数的图象与x轴交于,则关于x的一元一次方程的解为_______.
星期天,小明上午从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离千米与时间分钟的关系如图所示,则上午小明离家的距离是________千米.
已知直线,则它与x轴的交点A是________,与y轴的交点B是________,的面积为________.
三、解答题
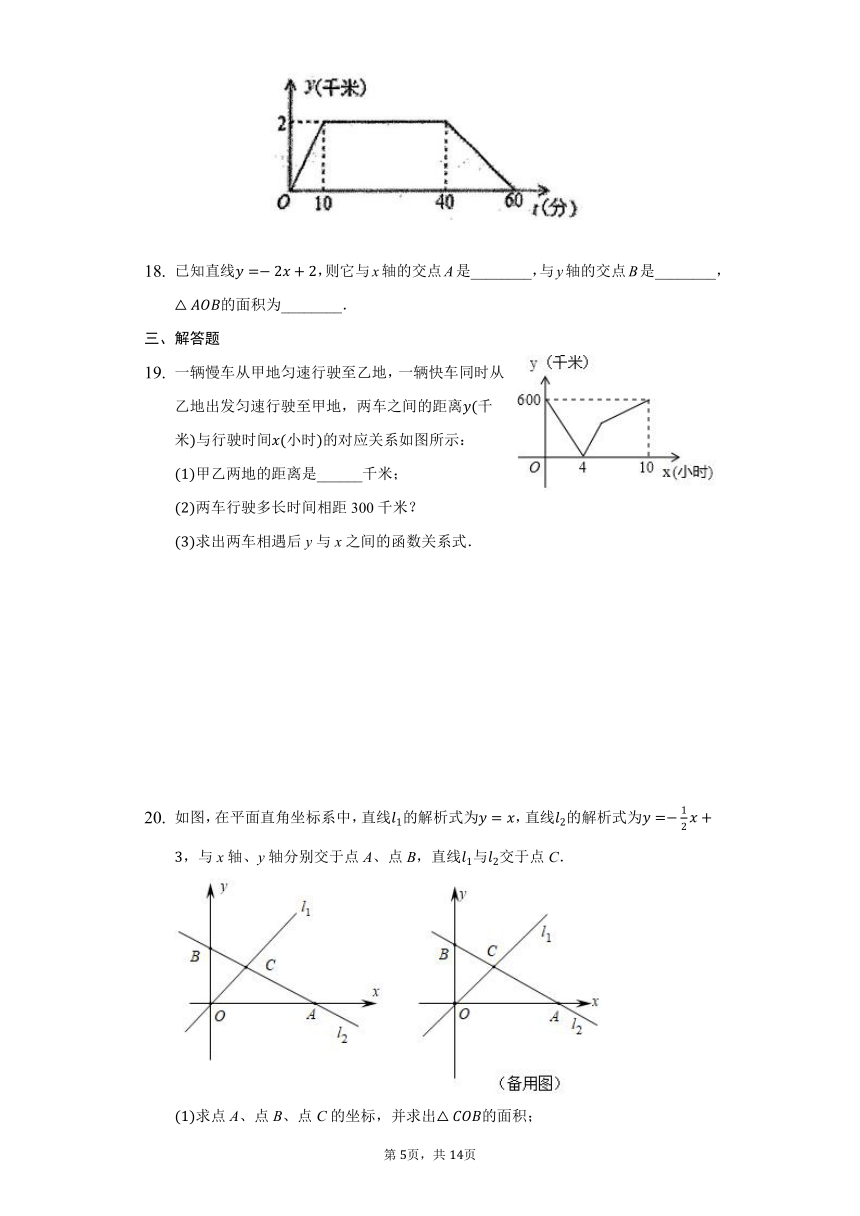
一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离千米与行驶时间小时的对应关系如图所示:
甲乙两地的距离是______千米;
两车行驶多长时间相距300千米?
求出两车相遇后y与x之间的函数关系式.
如图,在平面直角坐标系中,直线的解析式为,直线的解析式为,与x轴、y轴分别交于点A、点B,直线与交于点C.
求点A、点B、点C的坐标,并求出的面积;
若直线上存在点不与B重合,满足,请求出点P的坐标;
在y轴右侧有一动直线平行于y轴,分别与,交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的和表示甲,乙两车相对于出发地的距离与追赶时间之间的关系:
哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
甲,乙两车的速度分别是多少?
试分别确定甲,乙两车相对于出发地的距离与追赶时间之间的关系式;
乙车能在小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过210度时,按元度计费;月用电量超过210度时,其中的210度仍按元度计费,超过部分按元度计费.设每户家庭月用电量为x度时,应交电费y元.
分别求出当和时,y与x之间的关系式;
小明家5月份交电费元,则小明家这个月用电多少度?
答案和解析
1.【答案】A
【解析】解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,刚开始一段时间匀速,后来提速,继续做匀速运动,故正确;
乙用了3个小时到达目的地,故错误;
乙比甲晚出发1小时,故错误;
甲在出发4小时后被乙超过,故错误;
由上可得,正确是,
2.【答案】C
【解析】解:一次函数为常数且的图象经过点,
的解是,
,
则,
3.【答案】D
【解析】解:观察图象,可知轮船出发4小时后被快艇追上,所以错误的是第四个结论.
4.【答案】B
【解析】解:设,由图知,直线过,代入得:
,
解之得:
,
当时,即营销人员没有销售时的收入是300元.
5.【答案】A
【解答】
解:直线?经过点,
关于x的方程的解是,
故选A.
6.【答案】D
【解答】
解:两车的速度之差为,
,结论正确;
,
的值不确定,
值不确定,结论不正确;
两车相遇时间为,
,结论正确;
,,
,结论正确.
故选D.
7.【答案】A
【解析】解:直线和直线相交于点
方程的解为.
8.【答案】A
【解答】
解:方程的解,即为函数图象与x轴交点的横坐标,
直线过,
方程的解是,
故选A.
9.【答案】B
解:由表中的关系可得:弹簧长度y与称重x的关系是一次函数关系,
弹簧长度y与称重x的关系式为,
根据表中提供的数据得当时,,当时,,
,解得:
解析式为.
当弹簧最长时就是所挂重物最重时,
此时,
故弹簧最长为厘米.
故选B.
10.【答案】D
【解答】
解:由题意得,解得,函数的解析式为,
方程,即的解是,
故选:D.
11.【答案】C
【解答】
解:根据图表可得:当时,;
因而方程的解是.
故选:C.
12.【答案】C
【解答】
解:设,由图知,直线过,代入得:
解之得:
,
当时,.
即营销人员没有销售时的收入是300元.
故选C.
13.【答案】D
【解析】解:由图象知:
A.甲车的平均速度为,故A选项不合题意;
B.乙车的平均速度为,故B选项不合题意;
C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;
D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,
14.【答案】
【解析】解:观察函数的图象知:的图象经过点,
即当时,
所以关于x的方程的解为,
故答案为:.
15.【答案】
【解答】
解:根据题意得,,
即:.
故答案为.
16.【答案】
【解答】
解:一次函数的图象与x轴交于,
关于x的一元一次方程的解为.
故答案为.
17.【答案】
【解答】
解:设当时,距离千米与时间分钟的函数关系为,
图象经过,
解得:
与t的函数关系式为,
当时,,
故答案为.
18.【答案】,,?
1
【解答】
解:当时,有,,
即点A的坐标为;
当时,有,即点B的坐标为.
的面积.
故答案为,,1.
19.【答案】解:;
由题意得:慢车总用时10小时,
慢车速度为千米小时;
设快车速度为x千米小时,
由图象得:,
解得:,
快车速度为90千米小时;
设出发x小时后,两车相距300千米.
当两车没有相遇时,
由题意得:,解得:;
当两车相遇后,
由题意得:,解得:;
即两车行驶2或6小时时,两车相距300千米;
由图象得:小时,千米,
时间为小时时快车已到达甲地,此时慢车走了400千米,
两车相遇后y与x的函数关系式为.
20.【答案】解:直线的解析式为,与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为、,
联立式,并解得:,故点;
的面积;
设点,
,则,
则,
解得:或舍去,
故点;
设点M、N、Q的坐标分别为、、,
当时,
,,,
,,
≌,
,,
即:,,
解得:,;
当时,
则,即:,解得:,
;
当时,
同理可得:;
综上,点Q的坐标为或或
21.【答案】解:由函数图象,得
表示乙车离出发地的距离y与追赶时间x之间的关系;
甲车的速度为,乙车的速度为;
甲车的函数的关系式为:;
乙车的函数关系式为:;
设乙车行驶a小时可以追上甲车,由题意,得
,
解得:.
,
乙车不能在小时内追上甲车.
乙车追上甲车时,乙车行驶了2小时.
22.【答案】解:当时,y与x的函数解析式是;
当时,y与x的函数解析式:,
即;
因为小明家5月份的电费超过元,
所以把代入中,得.
答:小明家5月份用电210度.
第2页,共2页
第1页,共1页
一、选择题
A,B两地相距20km,甲乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程与行进时间之间的关系,有下列说法:
甲始终是匀速行进,乙的行进不是匀速的;
乙用了4个小时到达目的地;
乙比甲先出发1小时;
甲在出发4小时后被乙追上.
在这些说法中,正确的有
A.
1个
B.
2个
C.
3个
D.
4个
若一次函数为常数且的图象经过点,则关于x的方程的解为
A.
B.
C.
D.
如图,表示一艘轮船和一艘快艇沿相同路线从甲港岀发到乙港行驶路程随时间变化的图象.则下列结论错误的是
A.
轮船的速度为20千米时
B.
快艇的速度为40千米时
C.
轮船比快艇先出发2小时
D.
快艇到达乙港用了6小时
某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是
A.
310元
B.
300元
C.
290元
D.
280元
已知直线经过点和点,那么关于x的方程的解是
A.
B.
C.
D.
速度分别为和的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离与行驶时间之间的函数关系如图所示.下列说法:;;;若,则其中说法正确的是?
?
A.
B.
C.
D.
数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点P,根据图象可知,方程的解是???????????????????????????????
?????
?
A.
B.
C.
D.
如图,一次函数与x轴的交点为P,则关于x的方程的解为
A.
B.
2
C.
3
D.
有一个最多能称10千克的弹簧秤,称重发现,弹簧的长度与物体重量满足一定的关系,如下表.那么在弹簧秤的称重范围内,弹簧最长为
A.
10厘米
B.
厘米
C.
14厘米
D.
厘米
若一次函数b是常数,x与y的部分对应值如下表:
x
0
1
2
3
y
6
4
2
0
则方程的解是
A.
B.
C.
D.
已知一次函数b是常数且,x与y的部分对应值如下表:
x
0
1
2
3
y
6
4
2
0
那么方程的解是?
?
A.
B.
C.
D.
某公司市场营部的营销人员的个人收入与其每月的销售量满足一次函数关系,其图象如图所示,由图中给出的信息可知:销售量为零时,营销人员的收入是
A.
280元
B.
290元
C.
300元
D.
310元
甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是
A.
甲车的平均速度为
B.
乙车的平均速度为
C.
乙车比甲车先到B城
D.
乙车比甲车先出发1h
二、填空题
若一次函数的图象如图所示,点在函数图象上,则关于x的方程的解是______.
李明同学的家与学校的距离为2000米,如果他上学步行的速度为y米分,从家里到学校的时间为x分钟,则y与x之间的函数关系式为__________.
已知一次函数的图象与x轴交于,则关于x的一元一次方程的解为_______.
星期天,小明上午从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离千米与时间分钟的关系如图所示,则上午小明离家的距离是________千米.
已知直线,则它与x轴的交点A是________,与y轴的交点B是________,的面积为________.
三、解答题
一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离千米与行驶时间小时的对应关系如图所示:
甲乙两地的距离是______千米;
两车行驶多长时间相距300千米?
求出两车相遇后y与x之间的函数关系式.
如图,在平面直角坐标系中,直线的解析式为,直线的解析式为,与x轴、y轴分别交于点A、点B,直线与交于点C.
求点A、点B、点C的坐标,并求出的面积;
若直线上存在点不与B重合,满足,请求出点P的坐标;
在y轴右侧有一动直线平行于y轴,分别与,交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的和表示甲,乙两车相对于出发地的距离与追赶时间之间的关系:
哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
甲,乙两车的速度分别是多少?
试分别确定甲,乙两车相对于出发地的距离与追赶时间之间的关系式;
乙车能在小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过210度时,按元度计费;月用电量超过210度时,其中的210度仍按元度计费,超过部分按元度计费.设每户家庭月用电量为x度时,应交电费y元.
分别求出当和时,y与x之间的关系式;
小明家5月份交电费元,则小明家这个月用电多少度?
答案和解析
1.【答案】A
【解析】解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,刚开始一段时间匀速,后来提速,继续做匀速运动,故正确;
乙用了3个小时到达目的地,故错误;
乙比甲晚出发1小时,故错误;
甲在出发4小时后被乙超过,故错误;
由上可得,正确是,
2.【答案】C
【解析】解:一次函数为常数且的图象经过点,
的解是,
,
则,
3.【答案】D
【解析】解:观察图象,可知轮船出发4小时后被快艇追上,所以错误的是第四个结论.
4.【答案】B
【解析】解:设,由图知,直线过,代入得:
,
解之得:
,
当时,即营销人员没有销售时的收入是300元.
5.【答案】A
【解答】
解:直线?经过点,
关于x的方程的解是,
故选A.
6.【答案】D
【解答】
解:两车的速度之差为,
,结论正确;
,
的值不确定,
值不确定,结论不正确;
两车相遇时间为,
,结论正确;
,,
,结论正确.
故选D.
7.【答案】A
【解析】解:直线和直线相交于点
方程的解为.
8.【答案】A
【解答】
解:方程的解,即为函数图象与x轴交点的横坐标,
直线过,
方程的解是,
故选A.
9.【答案】B
解:由表中的关系可得:弹簧长度y与称重x的关系是一次函数关系,
弹簧长度y与称重x的关系式为,
根据表中提供的数据得当时,,当时,,
,解得:
解析式为.
当弹簧最长时就是所挂重物最重时,
此时,
故弹簧最长为厘米.
故选B.
10.【答案】D
【解答】
解:由题意得,解得,函数的解析式为,
方程,即的解是,
故选:D.
11.【答案】C
【解答】
解:根据图表可得:当时,;
因而方程的解是.
故选:C.
12.【答案】C
【解答】
解:设,由图知,直线过,代入得:
解之得:
,
当时,.
即营销人员没有销售时的收入是300元.
故选C.
13.【答案】D
【解析】解:由图象知:
A.甲车的平均速度为,故A选项不合题意;
B.乙车的平均速度为,故B选项不合题意;
C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;
D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,
14.【答案】
【解析】解:观察函数的图象知:的图象经过点,
即当时,
所以关于x的方程的解为,
故答案为:.
15.【答案】
【解答】
解:根据题意得,,
即:.
故答案为.
16.【答案】
【解答】
解:一次函数的图象与x轴交于,
关于x的一元一次方程的解为.
故答案为.
17.【答案】
【解答】
解:设当时,距离千米与时间分钟的函数关系为,
图象经过,
解得:
与t的函数关系式为,
当时,,
故答案为.
18.【答案】,,?
1
【解答】
解:当时,有,,
即点A的坐标为;
当时,有,即点B的坐标为.
的面积.
故答案为,,1.
19.【答案】解:;
由题意得:慢车总用时10小时,
慢车速度为千米小时;
设快车速度为x千米小时,
由图象得:,
解得:,
快车速度为90千米小时;
设出发x小时后,两车相距300千米.
当两车没有相遇时,
由题意得:,解得:;
当两车相遇后,
由题意得:,解得:;
即两车行驶2或6小时时,两车相距300千米;
由图象得:小时,千米,
时间为小时时快车已到达甲地,此时慢车走了400千米,
两车相遇后y与x的函数关系式为.
20.【答案】解:直线的解析式为,与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为、,
联立式,并解得:,故点;
的面积;
设点,
,则,
则,
解得:或舍去,
故点;
设点M、N、Q的坐标分别为、、,
当时,
,,,
,,
≌,
,,
即:,,
解得:,;
当时,
则,即:,解得:,
;
当时,
同理可得:;
综上,点Q的坐标为或或
21.【答案】解:由函数图象,得
表示乙车离出发地的距离y与追赶时间x之间的关系;
甲车的速度为,乙车的速度为;
甲车的函数的关系式为:;
乙车的函数关系式为:;
设乙车行驶a小时可以追上甲车,由题意,得
,
解得:.
,
乙车不能在小时内追上甲车.
乙车追上甲车时,乙车行驶了2小时.
22.【答案】解:当时,y与x的函数解析式是;
当时,y与x的函数解析式:,
即;
因为小明家5月份的电费超过元,
所以把代入中,得.
答:小明家5月份用电210度.
第2页,共2页
第1页,共1页
