华东师大版九年级下册第27章《圆》高分突破压轴专练(四)(Word版 含解析)
文档属性
| 名称 | 华东师大版九年级下册第27章《圆》高分突破压轴专练(四)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 18:51:37 | ||
图片预览



文档简介
华东师大版九下第27章《圆》
高分突破压轴专练(四)
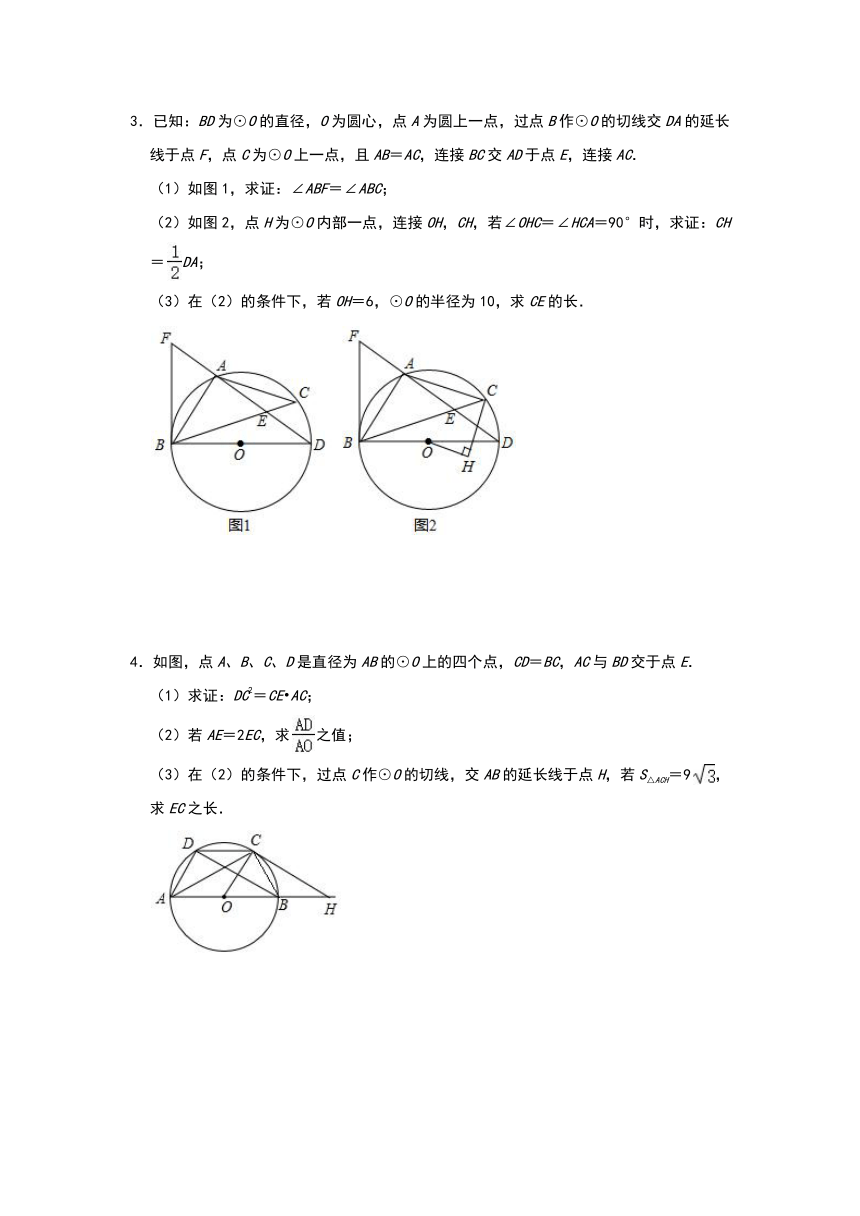
1.如图,以△ABC的边AB为直径的⊙O交AC的中点D,DE与⊙O相切,且交BC于E.若⊙O的直径为5,AC=8.求DE的长.
2.如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点M,DE的延长线与AC的延长线交于点N,连接AM.
(1)求证:AM=BM;
(2)若AM⊥BM,DE=8,∠N=15°,求BC的长.
3.已知:BD为⊙O的直径,O为圆心,点A为圆上一点,过点B作⊙O的切线交DA的延长线于点F,点C为⊙O上一点,且AB=AC,连接BC交AD于点E,连接AC.
(1)如图1,求证:∠ABF=∠ABC;
(2)如图2,点H为⊙O内部一点,连接OH,CH,若∠OHC=∠HCA=90°时,求证:CH=DA;
(3)在(2)的条件下,若OH=6,⊙O的半径为10,求CE的长.
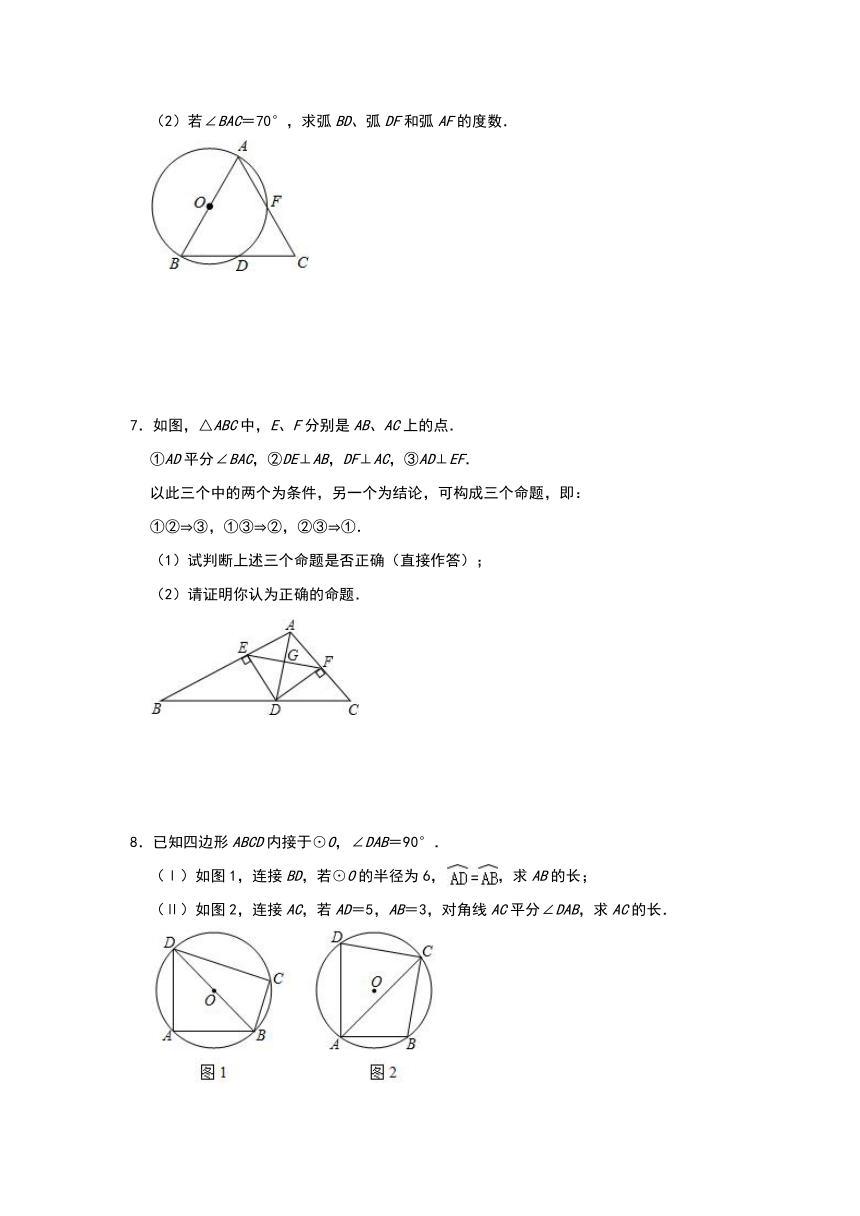
4.如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E.
(1)求证:DC2=CE?AC;
(2)若AE=2EC,求之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=9,求EC之长.
5.请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德(archimedes,公元前287﹣公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯Al﹣Binmi(973﹣1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al﹣Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,
∴MA=MC.
…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边△ABC内接于⊙O,AB=2,D为上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是
.
6.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?为什么?
(2)若∠BAC=70°,求弧BD、弧DF和弧AF的度数.
7.如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①②?③,①③?②,②③?①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
8.已知四边形ABCD内接于⊙O,∠DAB=90°.
(Ⅰ)如图1,连接BD,若⊙O的半径为6,,求AB的长;
(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.
9.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,交BC于F.
(1)若∠ABC=40°,∠C=80°,求∠CBD的度数;
(2)求证:DB=DE;
(3)若AB=6,AC=4,BC=5,求DE的长.
10.如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点E,且l∥BC.
(1)求证:AE平分∠BAC;
(2)作∠ABC的平分线BF交AE于点F,求证:BE=EF.
参考答案
1.解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,
∵D点为AC的中点,
∴BA=BC,AD=CD=AC=4,
∴∠A=∠C,
∵OA=OD,
∴∠A=∠ADO,
∴∠ADO=∠C,
∴OD∥BC,
∵DE与⊙O相切,
∴OD⊥DE,
∴BC⊥DE,
在Rt△ABD中,BD==3,
∵∠A=∠C,∠ADB=∠DEC=90°,
∴△ABD∽△CDE,
∴=,即=,
∴DE=.
2.(1)证明:
∵直径DE⊥AB于点F,
∴AF=BF,
∴AM=BM;
(2)连接AO,BO,如图,
由(1)可得
AM=BM,
∵AM⊥BM,
∴∠MAF=∠MBF=45°,
∴∠CMN=∠BMF=45°,
∵AO=BO,DE⊥AB,
∴∠AOF=∠BOF=,
∵∠N=15°,
∴∠ACM=∠CMN+∠N=60°,即∠ACB=60°,
∵∠ACB=.
∴∠AOF=∠ACB=60°.
∵DE=8,
∴AO=4.
方法1:在Rt△AOF中,OF=AO=2,AF==,
在Rt△AMF中,AM=BM==.
在Rt△ACM中,AC2=CM2+AM2,即(2CM)2=CM2+(2)2,解得CM=,
∴BC=CM+BM=+.
方法2:在Rt△AOF中,由sin∠AOF=,得AF=,
在Rt△AMF中,AM=BM==.
在Rt△ACM中,由,得CM=,
∴BC=CM+BM=+.
3.解:(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠D+∠ABD=90°,
∵FB是⊙O的切线,
∴∠FBD=90°,
∴∠FBA+∠ABD=90°,
∴∠FBA=∠D,
∵AB=AC,
∴∠C=∠ABC,
∵∠C=∠D,
∴∠ABF=∠ABC;
(2)如图2,连接OC,
∵∠OHC=∠HCA=90°,
∴AC∥OH,
∴∠ACO=∠COH,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC+∠CBO=∠ACB+∠OCB,
即∠ABD=∠ACO,
∴∠ABD=∠COH,
∵∠H=∠BAD=90°,
∴△ABD∽△HOC,
∴==2,
∴CH=DA;
(3)由(2)知,△ABD∽△HOC,
∴=2,
∵OH=6,⊙O的半径为10,
∴AB=2OH=12,BD=20,
∴AD==16,
在△ABF与△ABE中,,
∴△ABF≌△ABE,
∴BF=BE,AF=AE,
∵∠FBD=∠BAD=90°,
∴AB2=AF?AD,
∴AF==9,
∴AE=AF=9,
∴DE=7,BE==15,
∵AD,BC交于E,
∴AE?DE=BE?CE,
∴CE===.
4.解:(1)如图1,
∵CD=BC,
∴,
∴∠BDC=∠DAC,
∵∠DCE=∠ACD,
∴△CDE∽△CAD,
∴,
∴CD2=CE?AC;
(2)如图1,OC与BD的交点记作点F,设CE=x,
∵AE=2CE,
∴AE=2x,
∴AC=AE+CE=3x,
由(1)知,CD2=CE?AC,
∴CD2=x×3x=3x2,
∴CD=x,
∴BC=CD=x,
∵AB是⊙O的直径,
∴∠ACB=90°,
根据勾股定理得,AB==2x,
∴OA=OB=AB=x,
∴OB=OC=BC,
∴△BOC是等边三角形,
∵,
∴OC⊥BE,
∴OF=OB=x,
∵AB是⊙O的直径,
∴∠ADB=90°=∠OFB,
∴OF∥AD,
∵OA=OB,
∴AD=2OF=x,
∴==1;
(3)由(2)知,△BOC是等边三角形,
∴∠BOC=60°,
∵CH是⊙O的切线,
∴∠OCH=90°,
∴∠CHO=30°,
∴OH=2OC,
∵OH=OB+BH=OC+BH,
∴OB=BH,
∴OA=OB=BH,
∴S△ACH=3S△BOC=9,
∴S△BOC=3,
∵S△BOC=OB2=×(x)2=3,
∴x=﹣2(舍)或x=2,
∴EC=2.
5.(1)证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,
∴MA=MC.
在△MBA和△MGC中
∵,
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD;
(2)解:如图3,截取BF=CD,连接AF,AD,CD,
由题意可得:AB=AC,∠ABF=∠ACD,
在△ABF和△ACD中
∵,
∴△ABF≌ACD(SAS),
∴AF=AD,
∵AE⊥BD,
∴FE=DE,则CD+DE=BE,
∵∠ABD=45°,
∴BE==,
则△BDC的周长是2+2.
故答案为:2+2.
6.解:(1)AB=AC.
理由是:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
又∵DC=BD,
∴AB=AC;
(2)连接OD、OF.
∵△ABC中,AB=AC,∠BAC=70°,
∴∠ABC=∠C===55°,
∵OB=OD,
∴∠ODB=∠OBD=55°,
∴∠BOD=180°﹣∠B﹣∠ODB=180°﹣55°﹣55°=70°,
∴的度数是70°;
同理,∠AOF=40°,
则∠DOF=180°﹣∠AOF﹣∠BOD=180°﹣40°﹣70°=70°.
则的度数是70°,的度数是40°.
7.解:(1)①②?③,正确;①③?②,错误;②③?①,正确.
(2)先证①②?③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③?①.如图2,
设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=AD,OF=AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
8.解:(Ⅰ)如图1,
∵∠DAB=90°,
∴BD为直径,即BD=12,
∵,
∴AD=AB,
∴△ABD为等腰直角三角形,
∴AB=BD=6;
(Ⅱ)如图2,作BH⊥AC于H,
∵∠DAB=90°,
∴BD为直径,BD==,
∴∠BCD=90°,
∵AC平分∠DAB,
∴∠BAC=∠BAC=45°,
∴∠CBD=∠BDC=45°,
∴△CDB为等腰直角三角形,
∴BC=BD=×=,
在Rt△ABH中,AH=BH=AB=,
在Rt△BCH中,CH==,
∴AC=AH+CH=+=4.
9.解:(1)∵∠ABC=40°,∠C=80°,
∴∠BAC=180°﹣40°﹣80°=60°,
∵点E是△ABC的内心,
∴∠CAD=∠BAD=BAC=30°,
∴∠CBD=∠CAD=30°.
答:∠CBD的度数为30°;
(2)证明:如图,连接BE,
∴∠1=∠2,∠3=∠4,
∵∠2=∠6,
∴∠1=∠6,
∵∠5=∠1+∠3,
∠DBE=∠6+∠4=∠1+∠3,
∴∠5=∠DBE,
∴DB=DE;
(3)∵∠1=∠2,AB=6,AC=4,BC=5,
∴==,
∴BF=3,CF=2,
∵∠6=∠2,∠D=∠C,
∴△BDF∽△ACF,
∴===2,=,
∴DF=BD,
DF?AF=BF?CF=6,
∵∠1=∠2=∠6,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴=,
∴BD2=DF?DA=DF(AF+DF)=DF?AF+DF2=6+(BD)2,
解得BD=2,
∴DE=BD=2.
答:DE的长为2.
10.证明:(1)连接OE.
∵直线l与⊙O相切于E,
∴OE⊥l.
∵l∥BC,
∴OE⊥BC,
∴=,
∴∠BAE=∠CAE.
∴AE平分∠BAC;
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵=,
∴∠BAE=∠CBE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB,
∴BE=EF.
高分突破压轴专练(四)
1.如图,以△ABC的边AB为直径的⊙O交AC的中点D,DE与⊙O相切,且交BC于E.若⊙O的直径为5,AC=8.求DE的长.
2.如图,△ABC内接于⊙O,直径DE⊥AB于点F,交BC于点M,DE的延长线与AC的延长线交于点N,连接AM.
(1)求证:AM=BM;
(2)若AM⊥BM,DE=8,∠N=15°,求BC的长.
3.已知:BD为⊙O的直径,O为圆心,点A为圆上一点,过点B作⊙O的切线交DA的延长线于点F,点C为⊙O上一点,且AB=AC,连接BC交AD于点E,连接AC.
(1)如图1,求证:∠ABF=∠ABC;
(2)如图2,点H为⊙O内部一点,连接OH,CH,若∠OHC=∠HCA=90°时,求证:CH=DA;
(3)在(2)的条件下,若OH=6,⊙O的半径为10,求CE的长.
4.如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E.
(1)求证:DC2=CE?AC;
(2)若AE=2EC,求之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=9,求EC之长.
5.请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德(archimedes,公元前287﹣公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯Al﹣Binmi(973﹣1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al﹣Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,
∴MA=MC.
…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边△ABC内接于⊙O,AB=2,D为上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是
.
6.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?为什么?
(2)若∠BAC=70°,求弧BD、弧DF和弧AF的度数.
7.如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①②?③,①③?②,②③?①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
8.已知四边形ABCD内接于⊙O,∠DAB=90°.
(Ⅰ)如图1,连接BD,若⊙O的半径为6,,求AB的长;
(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.
9.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,交BC于F.
(1)若∠ABC=40°,∠C=80°,求∠CBD的度数;
(2)求证:DB=DE;
(3)若AB=6,AC=4,BC=5,求DE的长.
10.如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点E,且l∥BC.
(1)求证:AE平分∠BAC;
(2)作∠ABC的平分线BF交AE于点F,求证:BE=EF.
参考答案
1.解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,
∵D点为AC的中点,
∴BA=BC,AD=CD=AC=4,
∴∠A=∠C,
∵OA=OD,
∴∠A=∠ADO,
∴∠ADO=∠C,
∴OD∥BC,
∵DE与⊙O相切,
∴OD⊥DE,
∴BC⊥DE,
在Rt△ABD中,BD==3,
∵∠A=∠C,∠ADB=∠DEC=90°,
∴△ABD∽△CDE,
∴=,即=,
∴DE=.
2.(1)证明:
∵直径DE⊥AB于点F,
∴AF=BF,
∴AM=BM;
(2)连接AO,BO,如图,
由(1)可得
AM=BM,
∵AM⊥BM,
∴∠MAF=∠MBF=45°,
∴∠CMN=∠BMF=45°,
∵AO=BO,DE⊥AB,
∴∠AOF=∠BOF=,
∵∠N=15°,
∴∠ACM=∠CMN+∠N=60°,即∠ACB=60°,
∵∠ACB=.
∴∠AOF=∠ACB=60°.
∵DE=8,
∴AO=4.
方法1:在Rt△AOF中,OF=AO=2,AF==,
在Rt△AMF中,AM=BM==.
在Rt△ACM中,AC2=CM2+AM2,即(2CM)2=CM2+(2)2,解得CM=,
∴BC=CM+BM=+.
方法2:在Rt△AOF中,由sin∠AOF=,得AF=,
在Rt△AMF中,AM=BM==.
在Rt△ACM中,由,得CM=,
∴BC=CM+BM=+.
3.解:(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠D+∠ABD=90°,
∵FB是⊙O的切线,
∴∠FBD=90°,
∴∠FBA+∠ABD=90°,
∴∠FBA=∠D,
∵AB=AC,
∴∠C=∠ABC,
∵∠C=∠D,
∴∠ABF=∠ABC;
(2)如图2,连接OC,
∵∠OHC=∠HCA=90°,
∴AC∥OH,
∴∠ACO=∠COH,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC+∠CBO=∠ACB+∠OCB,
即∠ABD=∠ACO,
∴∠ABD=∠COH,
∵∠H=∠BAD=90°,
∴△ABD∽△HOC,
∴==2,
∴CH=DA;
(3)由(2)知,△ABD∽△HOC,
∴=2,
∵OH=6,⊙O的半径为10,
∴AB=2OH=12,BD=20,
∴AD==16,
在△ABF与△ABE中,,
∴△ABF≌△ABE,
∴BF=BE,AF=AE,
∵∠FBD=∠BAD=90°,
∴AB2=AF?AD,
∴AF==9,
∴AE=AF=9,
∴DE=7,BE==15,
∵AD,BC交于E,
∴AE?DE=BE?CE,
∴CE===.
4.解:(1)如图1,
∵CD=BC,
∴,
∴∠BDC=∠DAC,
∵∠DCE=∠ACD,
∴△CDE∽△CAD,
∴,
∴CD2=CE?AC;
(2)如图1,OC与BD的交点记作点F,设CE=x,
∵AE=2CE,
∴AE=2x,
∴AC=AE+CE=3x,
由(1)知,CD2=CE?AC,
∴CD2=x×3x=3x2,
∴CD=x,
∴BC=CD=x,
∵AB是⊙O的直径,
∴∠ACB=90°,
根据勾股定理得,AB==2x,
∴OA=OB=AB=x,
∴OB=OC=BC,
∴△BOC是等边三角形,
∵,
∴OC⊥BE,
∴OF=OB=x,
∵AB是⊙O的直径,
∴∠ADB=90°=∠OFB,
∴OF∥AD,
∵OA=OB,
∴AD=2OF=x,
∴==1;
(3)由(2)知,△BOC是等边三角形,
∴∠BOC=60°,
∵CH是⊙O的切线,
∴∠OCH=90°,
∴∠CHO=30°,
∴OH=2OC,
∵OH=OB+BH=OC+BH,
∴OB=BH,
∴OA=OB=BH,
∴S△ACH=3S△BOC=9,
∴S△BOC=3,
∵S△BOC=OB2=×(x)2=3,
∴x=﹣2(舍)或x=2,
∴EC=2.
5.(1)证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,
∴MA=MC.
在△MBA和△MGC中
∵,
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD;
(2)解:如图3,截取BF=CD,连接AF,AD,CD,
由题意可得:AB=AC,∠ABF=∠ACD,
在△ABF和△ACD中
∵,
∴△ABF≌ACD(SAS),
∴AF=AD,
∵AE⊥BD,
∴FE=DE,则CD+DE=BE,
∵∠ABD=45°,
∴BE==,
则△BDC的周长是2+2.
故答案为:2+2.
6.解:(1)AB=AC.
理由是:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
又∵DC=BD,
∴AB=AC;
(2)连接OD、OF.
∵△ABC中,AB=AC,∠BAC=70°,
∴∠ABC=∠C===55°,
∵OB=OD,
∴∠ODB=∠OBD=55°,
∴∠BOD=180°﹣∠B﹣∠ODB=180°﹣55°﹣55°=70°,
∴的度数是70°;
同理,∠AOF=40°,
则∠DOF=180°﹣∠AOF﹣∠BOD=180°﹣40°﹣70°=70°.
则的度数是70°,的度数是40°.
7.解:(1)①②?③,正确;①③?②,错误;②③?①,正确.
(2)先证①②?③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③?①.如图2,
设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=AD,OF=AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
8.解:(Ⅰ)如图1,
∵∠DAB=90°,
∴BD为直径,即BD=12,
∵,
∴AD=AB,
∴△ABD为等腰直角三角形,
∴AB=BD=6;
(Ⅱ)如图2,作BH⊥AC于H,
∵∠DAB=90°,
∴BD为直径,BD==,
∴∠BCD=90°,
∵AC平分∠DAB,
∴∠BAC=∠BAC=45°,
∴∠CBD=∠BDC=45°,
∴△CDB为等腰直角三角形,
∴BC=BD=×=,
在Rt△ABH中,AH=BH=AB=,
在Rt△BCH中,CH==,
∴AC=AH+CH=+=4.
9.解:(1)∵∠ABC=40°,∠C=80°,
∴∠BAC=180°﹣40°﹣80°=60°,
∵点E是△ABC的内心,
∴∠CAD=∠BAD=BAC=30°,
∴∠CBD=∠CAD=30°.
答:∠CBD的度数为30°;
(2)证明:如图,连接BE,
∴∠1=∠2,∠3=∠4,
∵∠2=∠6,
∴∠1=∠6,
∵∠5=∠1+∠3,
∠DBE=∠6+∠4=∠1+∠3,
∴∠5=∠DBE,
∴DB=DE;
(3)∵∠1=∠2,AB=6,AC=4,BC=5,
∴==,
∴BF=3,CF=2,
∵∠6=∠2,∠D=∠C,
∴△BDF∽△ACF,
∴===2,=,
∴DF=BD,
DF?AF=BF?CF=6,
∵∠1=∠2=∠6,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴=,
∴BD2=DF?DA=DF(AF+DF)=DF?AF+DF2=6+(BD)2,
解得BD=2,
∴DE=BD=2.
答:DE的长为2.
10.证明:(1)连接OE.
∵直线l与⊙O相切于E,
∴OE⊥l.
∵l∥BC,
∴OE⊥BC,
∴=,
∴∠BAE=∠CAE.
∴AE平分∠BAC;
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵=,
∴∠BAE=∠CBE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB,
∴BE=EF.
