华东师大版九年级下册第27章《圆》高分突破压轴专练(五)(Word版 含解析)
文档属性
| 名称 | 华东师大版九年级下册第27章《圆》高分突破压轴专练(五)(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览


文档简介
华东师大版九下第27章《圆》
高分突破压轴专练(五)
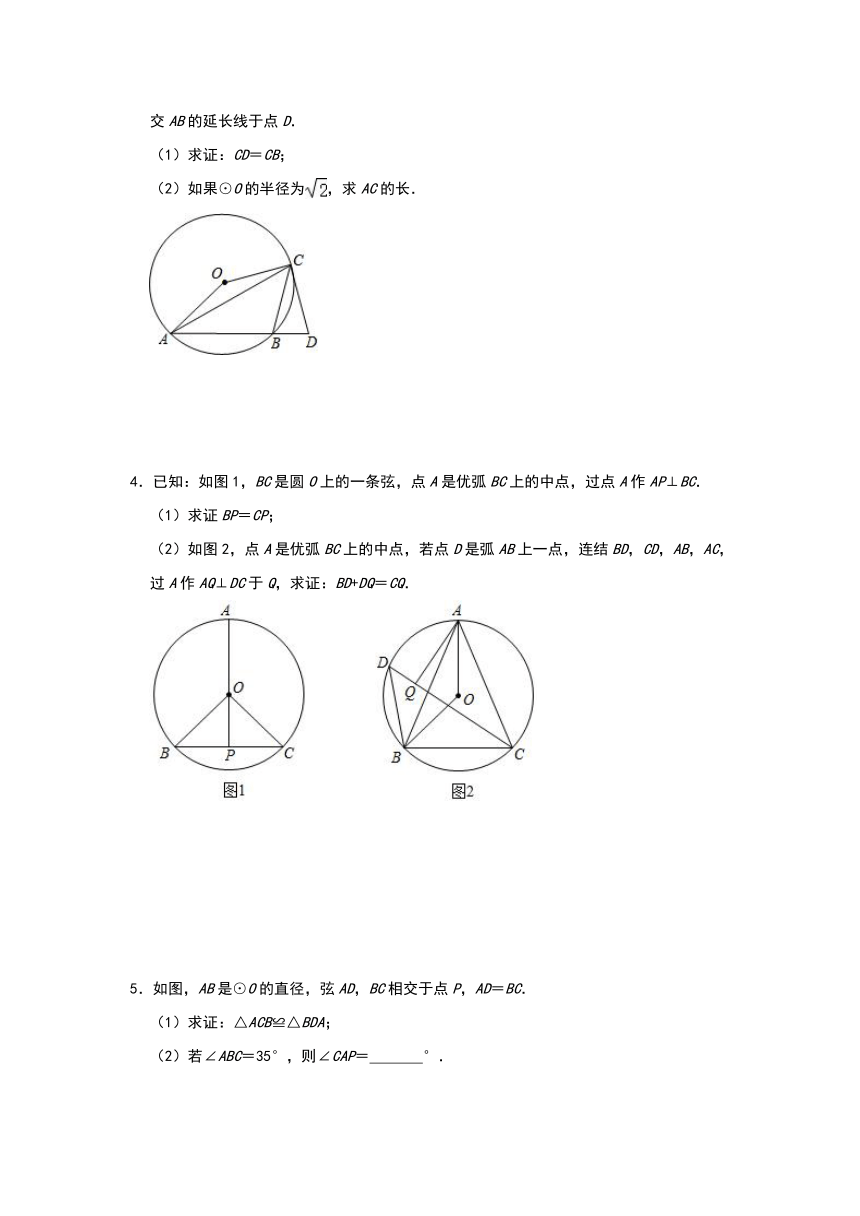
1.如图,已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于B.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为3,AB=4,求AD的长.
2.已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MN?MC=9,求BM的值.
3.如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
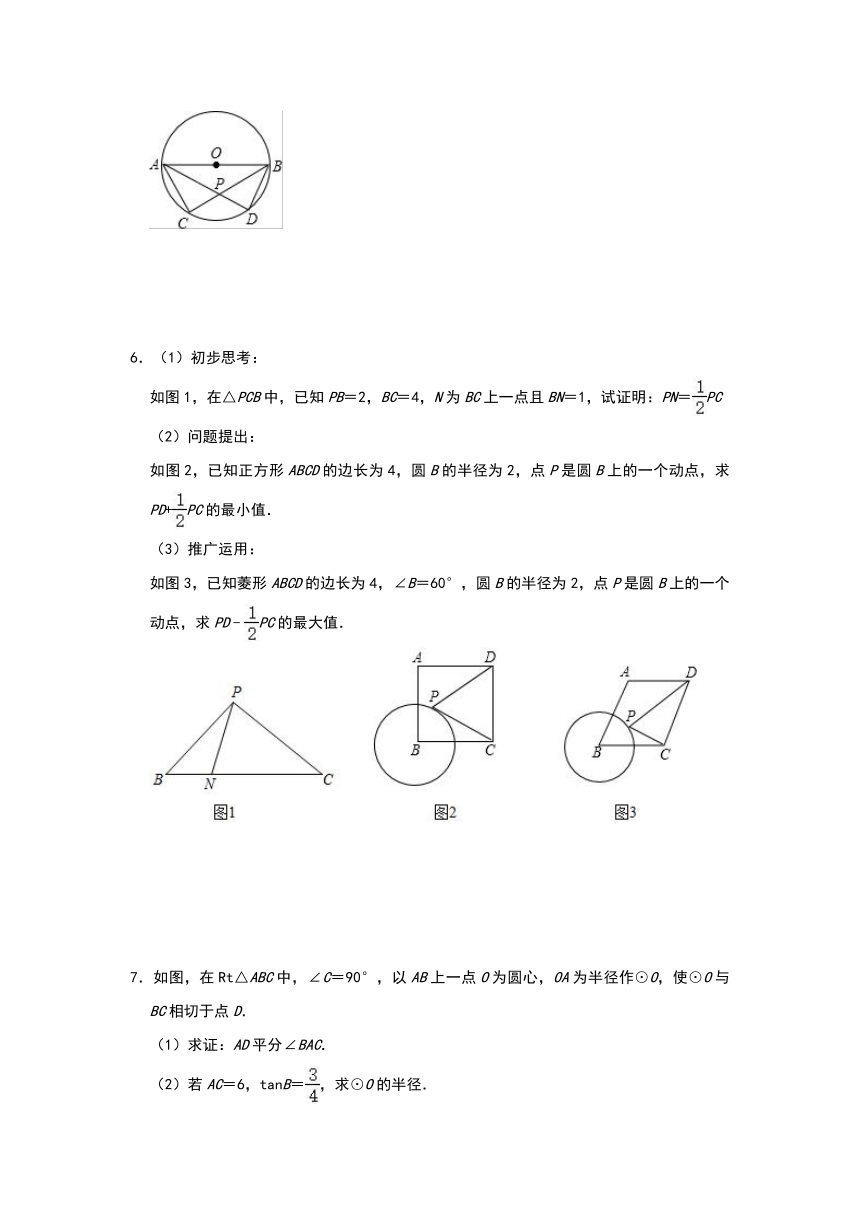
(1)求证:CD=CB;
(2)如果⊙O的半径为,求AC的长.
4.已知:如图1,BC是圆O上的一条弦,点A是优弧BC上的中点,过点A作AP⊥BC.
(1)求证BP=CP;
(2)如图2,点A是优弧BC上的中点,若点D是弧AB上一点,连结BD,CD,AB,AC,过A作AQ⊥DC于Q,求证:BD+DQ=CQ.
5.如图,AB是⊙O的直径,弦AD,BC相交于点P,AD=BC.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,则∠CAP= °.
6.(1)初步思考:
如图1,在△PCB中,已知PB=2,BC=4,N为BC上一点且BN=1,试证明:PN=PC
(2)问题提出:
如图2,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+PC的最小值.
(3)推广运用:
如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,求PD﹣PC的最大值.
7.如图,在Rt△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径作⊙O,使⊙O与BC相切于点D.
(1)求证:AD平分∠BAC.
(2)若AC=6,tanB=,求⊙O的半径.
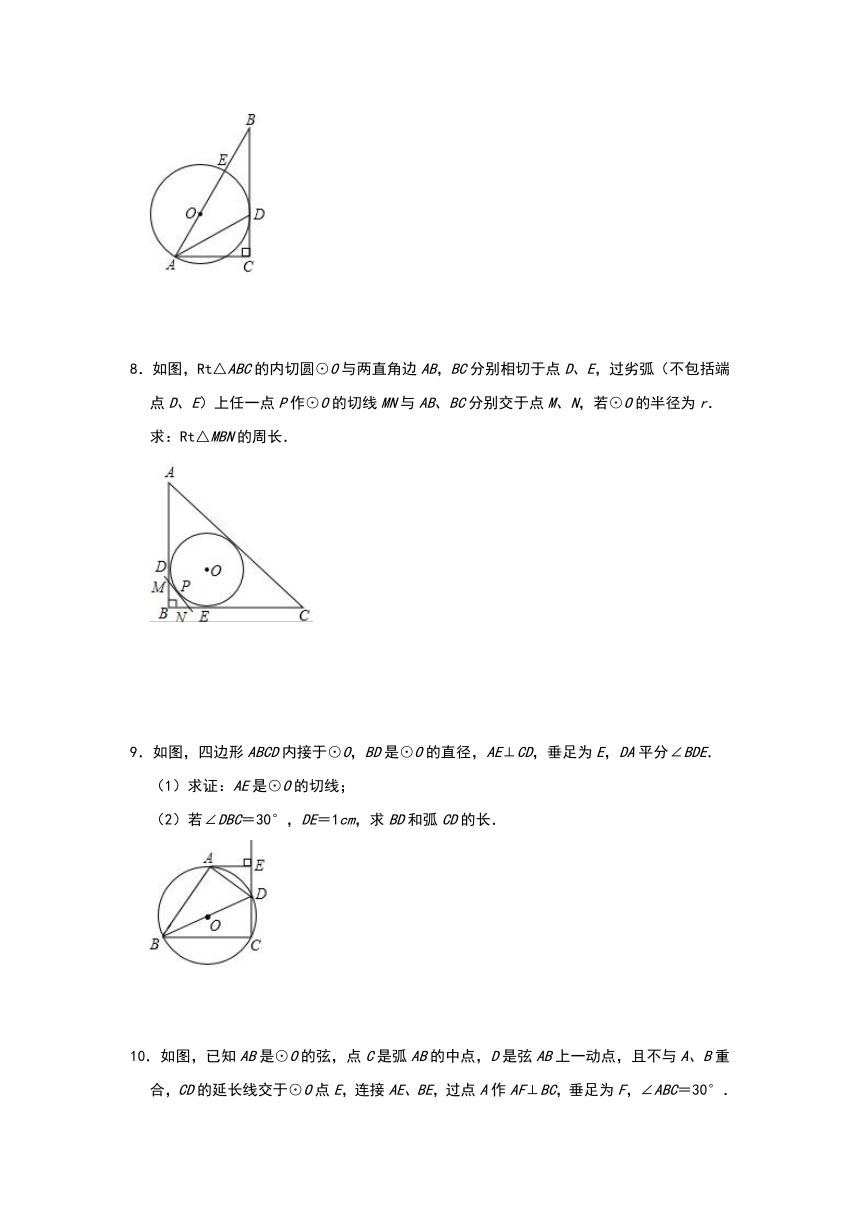
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN与AB、BC分别交于点M、N,若⊙O的半径为r.
求:Rt△MBN的周长.
9.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)若∠DBC=30°,DE=1cm,求BD和弧CD的长.
10.如图,已知AB是⊙O的弦,点C是弧AB的中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交于⊙O点E,连接AE、BE,过点A作AF⊥BC,垂足为F,∠ABC=30°.
(1)求证:AF是⊙O的切线;
(2)若BC=6,CD=3,则DE的长为 ;
(3)当点D在弦AB上运动时,的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
参考答案
1.(1)证明:如图,连接AO并延长交⊙O于点E,连接BE,则∠ABE=90°,
∴∠EAB+∠E=90°.
∵∠E=∠C,∠C=∠BAD,
∴∠EAB+∠BAD=90°.
∴AD是⊙O的切线.
(2)解:由(1)可知∠ABE=90°,直径AE=2AO=6,AB=4,
∴.
∵∠E=∠C=∠BAD,BD⊥AB,
∴cos∠BAD=cos∠E.
∴.
∴.
2.(1)①证明:如图1中,
∵OA=OC,
∴∠A=∠ACO,
∵∠PCB=∠A,
∴∠ACO=∠PCB,
∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线.
②∵CP=CA,
∴∠P=∠A,
∴∠COB=2∠A=2∠P,
∵∠OCP=90°,
∴∠P=30°,
∵OC=OA=2,
∴OP=2OC=4,
∴.
(2)解:如图2中,连接MA.
∵点M是弧AB的中点,
∴=,
∴∠ACM=∠BAM,
∵∠AMC=∠AMN,
∴△AMC∽△NMA,
∴,
∴AM2=MC?MN,
∵MC?MN=9,
∴AM=3,
∴BM=AM=3.
3.(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°﹣∠OBA﹣∠OBC=75°,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠D=360°﹣∠OBD﹣∠BOC﹣∠OCD=360°﹣(60°+75°)﹣60°﹣90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=OA=×=2,
∵CD是⊙O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴,
∴CD2=AD?BD=BD?(BD+AB),
∵CD=BC=OC=,
∴2=BD?(2+BD),
解得:BD=﹣1,
∴AC=AD=AB+BD=+1.
4.证明:(1)如图1中,连接AB,AC.
∵=,
∴AB=AC,
∵AP⊥BC,
∴BP=PC.
(2)如图2中,连接AD,在QC上截取QJ=QD,连接AJ.
∵AQ⊥DJ.QD=QJ,
∴AD=AJ,
∴∠ADJ=∠AJD,
∵AB=AC,
∴∠ABC=∠ACB=∠ADJ,∠AJD=∠ACJ+∠CAJ,
∵∠ACB=∠DCB+∠ACJ,
∴∠DCB+∠ACJ=∠ACJ+∠CAJ,
∴∠DCB=∠CAJ,
∵∠DCB=∠DAB,
∴∠DAB=∠CAJ,
∵AD=AJ,AB=AC,
∴△DAB≌△JAC(SAS),
∴BD=CJ,
∴BD+DQ=CJ+QJ=QC.
5.(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠BDA=90°.
在Rt△ACB与Rt△BDA中,
∵,
∴Rt△ACB≌Rt△BDA(HL);
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠ABC=35°,
∴∠BAC=90°﹣35°=55°.
∵Rt△ACB≌Rt△BDA,
∴=,
∴∠BAD=35°,
∴∠CAP=∠BAC﹣∠BAD=55°﹣35°=20°.
故答案为:20.
6.(1)证明:如图1,
∵PB=2,BC=4,BN=1,
∴PB2=4,BN?BC=4.
∴PB2=BN?BC.
∴=.
又∵∠B=∠B,
∴△BPN∽△BCP.
∴==.
∴PN=PC;
(2)如图2,在BC上取一点G,使得BG=1,
(3)同(2)中证法,如图3,
取BG=1,
当点P在DG的延长线上时,PD﹣PC的最大值,最大值为.
7.证明:(1)连接OD,
∵直线BC是⊙O的切线,
∴OD⊥BC,
∴∠ODB=∠C=90°,
∴OD∥AC,
∴∠CAD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠OAD,
即AD平分∠BAC;
(2)设OA=OD=r,CB=,
∴AB=,
∵∠C=∠ODB=90°,∠B为公共角,
∴△ACB∽△ODB,
∴,即,
解得:r=,
所以⊙O的半径为.
8.解:连接OD、OE.
∵AB和BC是⊙O的切线,
∴OD⊥AB,OE⊥BC,BD=BE,
则四边形DBEO是正方形.
∴BD=BE=r,
又∵MN是切线,
∴MP=MD,NP=NE,
∴Rt△MBN的周长=BM+BN+MN=BM+BN+MP+NP=BM+BN+DM+NE=BD+BE=2r.
9.(1)证明:连接OA,
∵DA平分∠BDE,
∴∠BDA=∠EDA.
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠EDA,
∴OA∥CE.
∵AE⊥CE,
∴AE⊥OA.
∴AE是⊙O的切线.
(2)解:∵BD是直径,
∴∠BCD=∠BAD=90°.
∵∠DBC=30°,∠BDC=60°,
∴∠BDE=120°.
∵DA平分∠BDE,
∴∠BDA=∠EDA=60°.
∴∠ABD=∠EAD=30°.
∵在Rt△AED中,∠AED=90°,∠EAD=30°,
∴AD=2DE.
∵在Rt△ABD中,∠BAD=90°,∠ABD=30°,
∴BD=2AD=4DE.
∵DE的长是1cm,
∴BD的长是4cm;
连接OC,
∴∠DOC=2∠DBC=60°,
∴的长==π.
10.(1)证明:如图1中,连接AC,OC,OA.
∵∠AOC=2∠ABC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠CAO=60°,
∵=,
∴AB⊥OC,
∴∠OAD=∠OAC=30°,
∵∠ABC=30°,
∴∠ABC=∠OAD,
∴OA∥BF,
∵AF⊥BF,
∴OA⊥AF,
∴AF是⊙O的切线.
(2)解:∵=,
∴∠CBD=∠BEC,
∵∠BCD=∠BCE,
∴△BCD∽△ECB,
∴=,
∴=,
∴EC=12,
∴DE=EC﹣CD=12﹣3=9.
故答案为9.
(3)解:结论:=,的值不变.
理由:如图2中,连接AC,OC,OC交AB于H,作AN∥EC交BE的延长线于N.
∵=,
∴OC⊥AB,CB=CA,
∴BH=AH=AB,
∵∠ABC=30°,
∴BH=BC,
∴AC=AB,
∵CE∥AN,
∴∠N=∠CEB=30°,∠EAN=∠AEC=∠ABC=30°,
∴∠CEA=∠ABC=30°,∠EAN=∠N,
∴∠N=∠AEC,AE=EN,
∵∠ACE=∠ABN,
∴△ACE∽△ABN,
∴==,
∴=,
∴的值不变.
高分突破压轴专练(五)
1.如图,已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于B.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为3,AB=4,求AD的长.
2.已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MN?MC=9,求BM的值.
3.如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
(1)求证:CD=CB;
(2)如果⊙O的半径为,求AC的长.
4.已知:如图1,BC是圆O上的一条弦,点A是优弧BC上的中点,过点A作AP⊥BC.
(1)求证BP=CP;
(2)如图2,点A是优弧BC上的中点,若点D是弧AB上一点,连结BD,CD,AB,AC,过A作AQ⊥DC于Q,求证:BD+DQ=CQ.
5.如图,AB是⊙O的直径,弦AD,BC相交于点P,AD=BC.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=35°,则∠CAP= °.
6.(1)初步思考:
如图1,在△PCB中,已知PB=2,BC=4,N为BC上一点且BN=1,试证明:PN=PC
(2)问题提出:
如图2,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+PC的最小值.
(3)推广运用:
如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,求PD﹣PC的最大值.
7.如图,在Rt△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径作⊙O,使⊙O与BC相切于点D.
(1)求证:AD平分∠BAC.
(2)若AC=6,tanB=,求⊙O的半径.
8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN与AB、BC分别交于点M、N,若⊙O的半径为r.
求:Rt△MBN的周长.
9.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)若∠DBC=30°,DE=1cm,求BD和弧CD的长.
10.如图,已知AB是⊙O的弦,点C是弧AB的中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交于⊙O点E,连接AE、BE,过点A作AF⊥BC,垂足为F,∠ABC=30°.
(1)求证:AF是⊙O的切线;
(2)若BC=6,CD=3,则DE的长为 ;
(3)当点D在弦AB上运动时,的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
参考答案
1.(1)证明:如图,连接AO并延长交⊙O于点E,连接BE,则∠ABE=90°,
∴∠EAB+∠E=90°.
∵∠E=∠C,∠C=∠BAD,
∴∠EAB+∠BAD=90°.
∴AD是⊙O的切线.
(2)解:由(1)可知∠ABE=90°,直径AE=2AO=6,AB=4,
∴.
∵∠E=∠C=∠BAD,BD⊥AB,
∴cos∠BAD=cos∠E.
∴.
∴.
2.(1)①证明:如图1中,
∵OA=OC,
∴∠A=∠ACO,
∵∠PCB=∠A,
∴∠ACO=∠PCB,
∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线.
②∵CP=CA,
∴∠P=∠A,
∴∠COB=2∠A=2∠P,
∵∠OCP=90°,
∴∠P=30°,
∵OC=OA=2,
∴OP=2OC=4,
∴.
(2)解:如图2中,连接MA.
∵点M是弧AB的中点,
∴=,
∴∠ACM=∠BAM,
∵∠AMC=∠AMN,
∴△AMC∽△NMA,
∴,
∴AM2=MC?MN,
∵MC?MN=9,
∴AM=3,
∴BM=AM=3.
3.(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°﹣∠OBA﹣∠OBC=75°,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠D=360°﹣∠OBD﹣∠BOC﹣∠OCD=360°﹣(60°+75°)﹣60°﹣90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=OA=×=2,
∵CD是⊙O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴,
∴CD2=AD?BD=BD?(BD+AB),
∵CD=BC=OC=,
∴2=BD?(2+BD),
解得:BD=﹣1,
∴AC=AD=AB+BD=+1.
4.证明:(1)如图1中,连接AB,AC.
∵=,
∴AB=AC,
∵AP⊥BC,
∴BP=PC.
(2)如图2中,连接AD,在QC上截取QJ=QD,连接AJ.
∵AQ⊥DJ.QD=QJ,
∴AD=AJ,
∴∠ADJ=∠AJD,
∵AB=AC,
∴∠ABC=∠ACB=∠ADJ,∠AJD=∠ACJ+∠CAJ,
∵∠ACB=∠DCB+∠ACJ,
∴∠DCB+∠ACJ=∠ACJ+∠CAJ,
∴∠DCB=∠CAJ,
∵∠DCB=∠DAB,
∴∠DAB=∠CAJ,
∵AD=AJ,AB=AC,
∴△DAB≌△JAC(SAS),
∴BD=CJ,
∴BD+DQ=CJ+QJ=QC.
5.(1)证明:∵AB是⊙O的直径,
∴∠ACB=∠BDA=90°.
在Rt△ACB与Rt△BDA中,
∵,
∴Rt△ACB≌Rt△BDA(HL);
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠ABC=35°,
∴∠BAC=90°﹣35°=55°.
∵Rt△ACB≌Rt△BDA,
∴=,
∴∠BAD=35°,
∴∠CAP=∠BAC﹣∠BAD=55°﹣35°=20°.
故答案为:20.
6.(1)证明:如图1,
∵PB=2,BC=4,BN=1,
∴PB2=4,BN?BC=4.
∴PB2=BN?BC.
∴=.
又∵∠B=∠B,
∴△BPN∽△BCP.
∴==.
∴PN=PC;
(2)如图2,在BC上取一点G,使得BG=1,
(3)同(2)中证法,如图3,
取BG=1,
当点P在DG的延长线上时,PD﹣PC的最大值,最大值为.
7.证明:(1)连接OD,
∵直线BC是⊙O的切线,
∴OD⊥BC,
∴∠ODB=∠C=90°,
∴OD∥AC,
∴∠CAD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CAD=∠OAD,
即AD平分∠BAC;
(2)设OA=OD=r,CB=,
∴AB=,
∵∠C=∠ODB=90°,∠B为公共角,
∴△ACB∽△ODB,
∴,即,
解得:r=,
所以⊙O的半径为.
8.解:连接OD、OE.
∵AB和BC是⊙O的切线,
∴OD⊥AB,OE⊥BC,BD=BE,
则四边形DBEO是正方形.
∴BD=BE=r,
又∵MN是切线,
∴MP=MD,NP=NE,
∴Rt△MBN的周长=BM+BN+MN=BM+BN+MP+NP=BM+BN+DM+NE=BD+BE=2r.
9.(1)证明:连接OA,
∵DA平分∠BDE,
∴∠BDA=∠EDA.
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠EDA,
∴OA∥CE.
∵AE⊥CE,
∴AE⊥OA.
∴AE是⊙O的切线.
(2)解:∵BD是直径,
∴∠BCD=∠BAD=90°.
∵∠DBC=30°,∠BDC=60°,
∴∠BDE=120°.
∵DA平分∠BDE,
∴∠BDA=∠EDA=60°.
∴∠ABD=∠EAD=30°.
∵在Rt△AED中,∠AED=90°,∠EAD=30°,
∴AD=2DE.
∵在Rt△ABD中,∠BAD=90°,∠ABD=30°,
∴BD=2AD=4DE.
∵DE的长是1cm,
∴BD的长是4cm;
连接OC,
∴∠DOC=2∠DBC=60°,
∴的长==π.
10.(1)证明:如图1中,连接AC,OC,OA.
∵∠AOC=2∠ABC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠CAO=60°,
∵=,
∴AB⊥OC,
∴∠OAD=∠OAC=30°,
∵∠ABC=30°,
∴∠ABC=∠OAD,
∴OA∥BF,
∵AF⊥BF,
∴OA⊥AF,
∴AF是⊙O的切线.
(2)解:∵=,
∴∠CBD=∠BEC,
∵∠BCD=∠BCE,
∴△BCD∽△ECB,
∴=,
∴=,
∴EC=12,
∴DE=EC﹣CD=12﹣3=9.
故答案为9.
(3)解:结论:=,的值不变.
理由:如图2中,连接AC,OC,OC交AB于H,作AN∥EC交BE的延长线于N.
∵=,
∴OC⊥AB,CB=CA,
∴BH=AH=AB,
∵∠ABC=30°,
∴BH=BC,
∴AC=AB,
∵CE∥AN,
∴∠N=∠CEB=30°,∠EAN=∠AEC=∠ABC=30°,
∴∠CEA=∠ABC=30°,∠EAN=∠N,
∴∠N=∠AEC,AE=EN,
∵∠ACE=∠ABN,
∴△ACE∽△ABN,
∴==,
∴=,
∴的值不变.
