华东师大版九年级下册数学 27.2.2 直线与圆的位置关系 同步练习(word含解析)
文档属性
| 名称 | 华东师大版九年级下册数学 27.2.2 直线与圆的位置关系 同步练习(word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 228.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 00:00:00 | ||
图片预览



文档简介
27.2.2 直线与圆的位置关系 同步练习
一.选择题
1.已知⊙O的半径是10,圆心O到直线l的距离是13,则直线l与⊙O的位置关系是( )
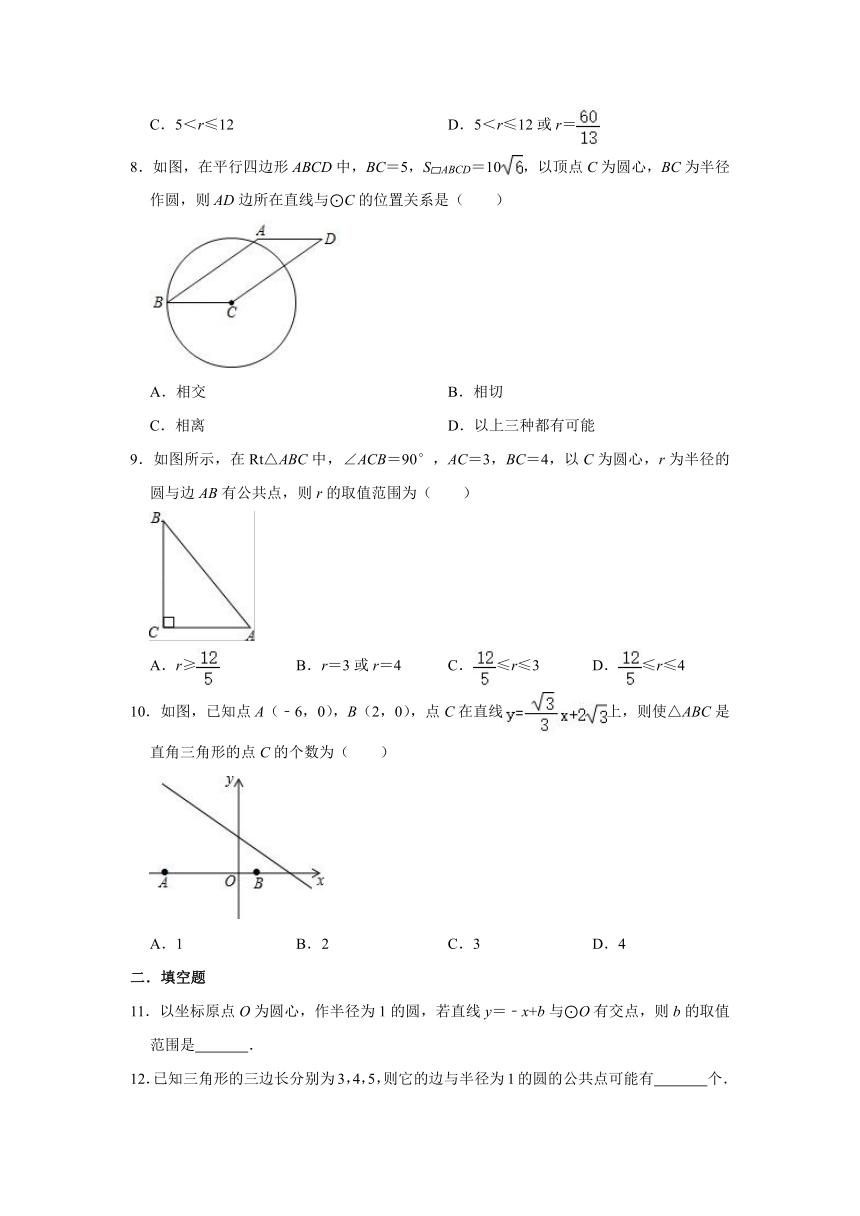
A.相离 B.相交 C.相切 D.无法确定
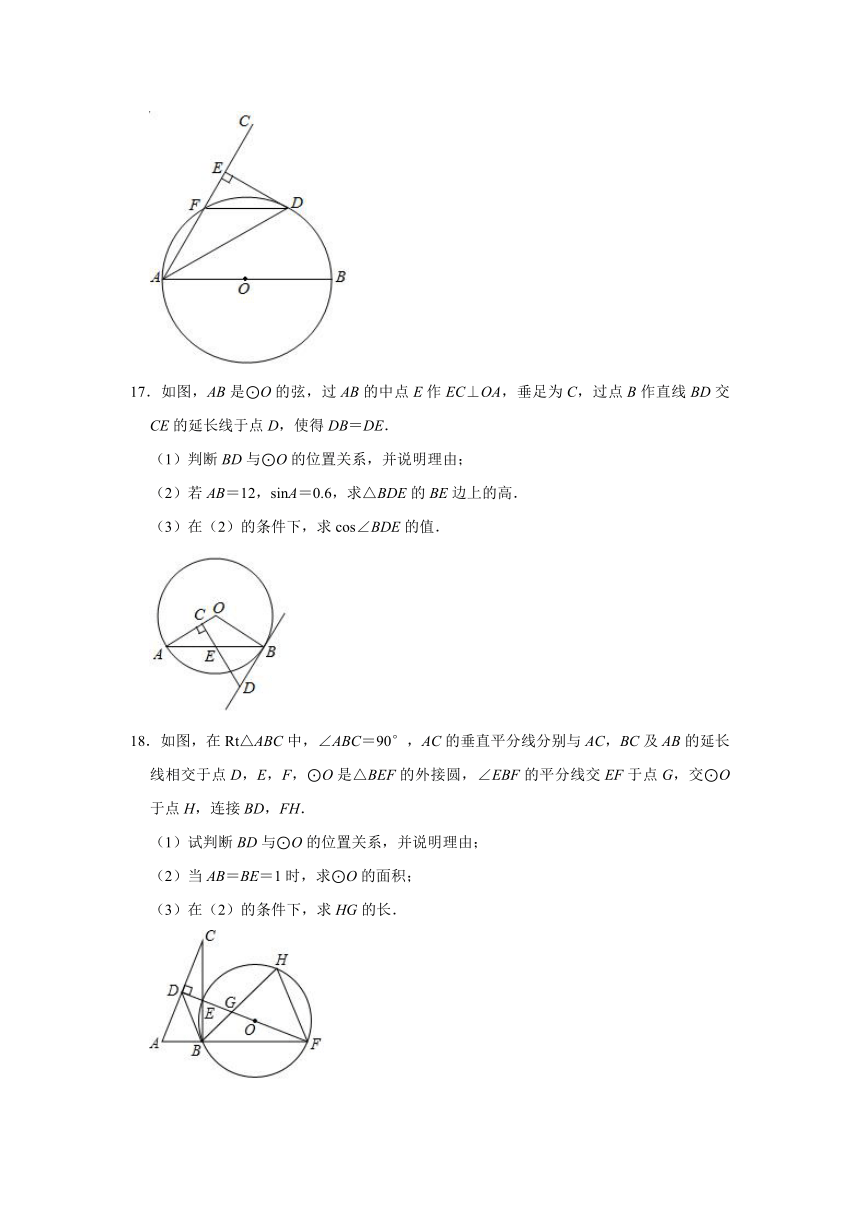
2.若直线l与半径为10的⊙O相交,则圆心O与直线l的距离d为( )
A.d<10 B.d>10 C.d=10 D.d≤10
3.圆的直径是8cm,若圆心与直线的距离是4cm,则该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
4.在Rt△ABC中,∠ACB=90°,AC=3,BC=4.点O为边AB上一点(不与A重合)⊙O是以点O为圆心,AO为半径的圆.当⊙O与三角形边的交点个数为3时,则OA的范围( )
A.0<OA≤或2.5≤OA<5 B.0<OA或OA=2.5
C.OA=2.5 D.OA=2.5或
5.平面直角坐标系中有点A(3,4),以A为圆心,5为半径画圆,在同一坐标系中直线y=﹣x与⊙A的位置关系是( )
A.相离 B.相切
C.相交 D.以上情况都有可能
6.已知⊙O1、⊙O2、⊙O3、⊙O4是四个半径为3的等圆,在这四个圆中,若某圆的圆心到直线l的距离为6,则这个圆可能是( )
A.⊙O1 B.⊙O2 C.⊙O3 D.⊙O4
7.在Rt△ABC中,∠C=90°,AC=5,BC=12.若以C为圆心,r为半径的圆与斜边AB只有一个公共点,则半径r的值或取值范围是( )
A. B.5≤r≤12或r=
C.5<r≤12 D.5<r≤12或r=
8.如图,在平行四边形ABCD中,BC=5,S?ABCD=10,以顶点C为圆心,BC为半径作圆,则AD边所在直线与⊙C的位置关系是( )
A.相交 B.相切
C.相离 D.以上三种都有可能
9.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心,r为半径的圆与边AB有公共点,则r的取值范围为( )
A.r≥ B.r=3或r=4 C.≤r≤3 D.≤r≤4
10.如图,已知点A(﹣6,0),B(2,0),点C在直线上,则使△ABC是直角三角形的点C的个数为( )
A.1 B.2 C.3 D.4
二.填空题
11.以坐标原点O为圆心,作半径为1的圆,若直线y=﹣x+b与⊙O有交点,则b的取值范围是 .
12.已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点可能有 个.
13.直线y=kx+6k交x轴于点A,交y轴于点B,以原点O为圆心,3为半径的⊙O与l相交,则k的取值范围为 .
14.如图,矩形ABCD中,AB=4,BC=6,E是边BC的中点,点P在边AD上,设DP=x,若以点D为圆心,DP为半径的⊙D与线段AE只有一个公共点,则所有满足条件的x的取值范围是 .
15.如图,坐标平面内,矩形AOCD的顶点A(0,2)、C(4,0)、D(4,2),抛物线y=x2﹣1经过点Q(a,4),P(b,4),⊙P的半径为1,当圆心P在抛物线上从点P运动到点Q,则在整个运动过程中,⊙P与矩形AOCD只有一个公共点的情况共出现 次.
三.解答题
16.如图,AB是⊙O的直径,AC与⊙O交于F,弦AD平分∠CAB,DE⊥AC,垂足为E.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径为3,若∠CAB=60°,求线段EF.
17.如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若AB=12,sinA=0.6,求△BDE的BE边上的高.
(3)在(2)的条件下,求cos∠BDE的值.
18.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG的长.
参考答案
一.选择题
1.解:∵⊙O的半径为10,圆心O到直线l的距离是13,而10<13,
∴点O到直线l的距离大于半径,
∴直线l与⊙O相离.
故选:A.
2.解:∵⊙O的半径为10,直线l与⊙O相交,
∴圆心到直线的距离小于圆的半径,
即d<10.
故选:A.
3.解:∵⊙O的直径为8cm,
∴r=4cm,
∵d=4cm,
∴d=r,
∴直线l与⊙O的位置关系是相切.
故选:B.
4.解:如右图所示,
当圆心从O1到O3的过程中,⊙O与三角形边的交点个数为3,当恰好到达O3时则变为4个交点,
作O3D⊥BC于点D,
则∠O3BD=∠ABC,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
设O3A=a,则O3B=5﹣a,
∴,得a=,
∴当0<OA时,⊙O与三角形边的交点个数为3,
当点O为AB的中点时,⊙O与三角形边的交点个数为3,此时OA=2.5,
由上可得,0<OA或OA=2.5时,⊙O与三角形边的交点个数为3,
故选:B.
5.解:如图,
∵A(3,4),∴AO=5,
∵点A到直线y=﹣x的距离为AB的长小于圆的半径r,即AB<AO,
∴直线y=﹣x与⊙A的位置关系是相交,
故选:C.
6.解:∵⊙O1、⊙O2、⊙O3、⊙O4是四个半径为3的等圆,
∴圆心到直线l的距离为6是⊙O2,
故选:B.
7.解:∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=13.
分两种情况:
(1)圆与AB相切时,即r=CD=5×12÷13=;
(2)点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即5<r≤12.
故选:D.
8.解:如图,作CH⊥DA交DA的延长线于H.
∵S平行四边形ABCD=BC?CH,
∴CH==2,
∵2<5,
∴直线AD与⊙C相交,
故选:A.
9.解:作CD⊥AB于D,如图所示:
∵∠C=90°,AC=3,BC=4,
∴AB==5,
∵△ABC的面积=AB?CD=AC?BC,
∴CD===,
即圆心C到AB的距离d=,
∵AC<BC,
∴以C为圆心,r=或4为半径所作的圆与斜边AB只有一个公共点,
∴若⊙C与斜边AB有公共点,则r的取值范围是≤r≤4.
故选:D.
10.解:如图,
①当∠A为直角时,过点A作垂线与直线的交点W(﹣6,4),
②当∠B为直角时,过点B作垂线与直线的交点S(2,),
③若∠C为直角,
则点C在以线段AB为直径、AB中点E(﹣2,0)为圆心、4为半径的圆与直线的交点上.
在直线中,当x=0时y=2,即Q(0,2),
当y=0时x=6,即点P(6,0),
则PQ==4,
过AB中点E(﹣2,0),作EF⊥直线l于点F,
则∠EFP=∠QOP=90°,
∵∠EPF=∠QPO,
∴△EFP∽△QOP,
∴=,即=,
解得:EF=4,
∴以线段AB为直径、E(﹣2,0)为圆心的圆与直线恰好有一个交点.
所以直线上有一点C满足∠C=90°.
综上所述,使△ABC是直角三角形的点C的个数为3,
故选:C.
二.填空题
11.解:当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=1.
则OB=OC=.即b=;
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣.
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣≤b≤.
故答案为﹣≤b≤.
12.解:∵32+42=25,52=25,
∴三角形为直角三角形,
设内切圆半径为r,则(3+4+5)r=×3×4,
解得r=1,
所以应分为五种情况:
当一条边与圆相离时,有0个交点,
当一条边与圆相切时,有1个交点,
当一条边与圆相交时,有2个交点,
当圆与三角形内切圆时,有3个交点,
当两条边与圆同时相交时,有4个交点,
故公共点个数可能为0或1或2或3或4个.
故答案为0或1或2或3或4.
13.解:∵直线y=kx+6k交x轴于点A,交y轴于点B,
∴A(﹣6,0),B(0,6k),
设⊙O与AB相切于C,
连接OC,
∴OA=6,OC=3,∠ACO=90°,
∴OC=OA,
∴∠OAC=30°,
当⊙O与l相交时,OB=|6k|>2,
∴﹣<k<,
故答案为﹣<k<.
14.解:如图,当⊙D与AE相切时,设切点为G,连接DG,
∵PD=DG=x,
∵∠DAG=∠AEB,∠AGD=∠B=90°,
∴△AGD∽△EBA,
∴=,
∴=,
x=,
当⊙D过点E时,如图,⊙D与线段有两个公共点,连接DE,此时PD=DE=5,
∴当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,x满足的条件:x=或5<x≤6;
故答案为:x=或5<x≤6.
15.解:由题意抛物线y=x2﹣1与x轴的交点为(﹣1,0),(1,0),与y轴的交点为(0,﹣1).
观察图形可知当⊙P在AD上方与AD相切时,⊙P与矩形AOCD只有一个公共点,
当点P运动到(0,﹣1)时,⊙P与矩形AOCD只有一个公共点,
当点P运动到(﹣1,0)时,⊙P与矩形AOCD只有一个公共点,
∵OA=2,
∴⊙P在AD与OC中间时,不存在满足条件的⊙P,
综上所述,⊙P与矩形AOCD只有一个公共点的情况有3种情形,
故答案为3.
三.解答题
16.解:(1)直线DE与⊙O相切,理由如下:
连结OD.
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)过O作OG⊥AF于G,
∴AF=2AG,
∵∠BAC=60°,OA=3,
∴AG=OA=,
∴AF=3,
∴AF=OD,
∴四边形AODF是菱形,
∴DF∥OA,DF=OA=3,
∴∠EFD=∠BAC=60°,
∴EF=DF=.
17.解:(1)BD与⊙O相切,理由如下:
∵OA=OB,DB=DE,
∴∠A=∠OBA,∠DEB=∠DBE.
∵EC⊥OA,∠DEB=∠AEC,
∴∠A+∠DEB=90°,
∴∠OBA+∠DEB=90°,
∴∠OBD=90°.
∵OB是⊙O的半径,
∴BD与⊙O相切;
(2)过点D作DF⊥AB于点F,连接OE,如图:
∵点E是AB的中点,AB=12,
∴AE=EB=6,OE⊥AB.
又∵DF⊥AB,EC⊥OA,
∴∠EDF=∠A,
∵sinA=0.6,
∴sin∠EDF=0.6,
∵DB=DE,DF⊥AB,
∴EF==3,
∵sin∠EDF=,
∴=0.6,
∴ED=DB=5.
∴由勾股定理得:DF==4.
∴△BDE的BE边上的高为4.
(3)过点E作EH⊥DB于点H,
则S△EBD==,
∵EB=6,DF=4,DB=5,
∴EH=.
由勾股定理得:DH==,
∴cos∠BDE==.
18.解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,∠EBF=90°,
∴∠C=∠DBC,EF为直径,
∴点O在EF上,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF(ASA),
∵BC=BF,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴EF==,
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=(EF)2?π=π=π;
(3)∵AB=BE,∠ABE=90°,
∴∠AEB=45°,
∵EA=EC,
∴∠C=22.5°,
∴∠H=∠BEG=∠CED=90°﹣22.5°=67.5°,
∵BH平分∠CBF,
∴∠EBG=∠HBF=45°,
∴∠BGE=∠BFH=67.5°,
∴BG=BE=1,BH=BF=1+,
∴HG=BH﹣BG=.
一.选择题
1.已知⊙O的半径是10,圆心O到直线l的距离是13,则直线l与⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
2.若直线l与半径为10的⊙O相交,则圆心O与直线l的距离d为( )
A.d<10 B.d>10 C.d=10 D.d≤10
3.圆的直径是8cm,若圆心与直线的距离是4cm,则该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
4.在Rt△ABC中,∠ACB=90°,AC=3,BC=4.点O为边AB上一点(不与A重合)⊙O是以点O为圆心,AO为半径的圆.当⊙O与三角形边的交点个数为3时,则OA的范围( )
A.0<OA≤或2.5≤OA<5 B.0<OA或OA=2.5
C.OA=2.5 D.OA=2.5或
5.平面直角坐标系中有点A(3,4),以A为圆心,5为半径画圆,在同一坐标系中直线y=﹣x与⊙A的位置关系是( )
A.相离 B.相切
C.相交 D.以上情况都有可能
6.已知⊙O1、⊙O2、⊙O3、⊙O4是四个半径为3的等圆,在这四个圆中,若某圆的圆心到直线l的距离为6,则这个圆可能是( )
A.⊙O1 B.⊙O2 C.⊙O3 D.⊙O4
7.在Rt△ABC中,∠C=90°,AC=5,BC=12.若以C为圆心,r为半径的圆与斜边AB只有一个公共点,则半径r的值或取值范围是( )
A. B.5≤r≤12或r=
C.5<r≤12 D.5<r≤12或r=
8.如图,在平行四边形ABCD中,BC=5,S?ABCD=10,以顶点C为圆心,BC为半径作圆,则AD边所在直线与⊙C的位置关系是( )
A.相交 B.相切
C.相离 D.以上三种都有可能
9.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以C为圆心,r为半径的圆与边AB有公共点,则r的取值范围为( )
A.r≥ B.r=3或r=4 C.≤r≤3 D.≤r≤4
10.如图,已知点A(﹣6,0),B(2,0),点C在直线上,则使△ABC是直角三角形的点C的个数为( )
A.1 B.2 C.3 D.4
二.填空题
11.以坐标原点O为圆心,作半径为1的圆,若直线y=﹣x+b与⊙O有交点,则b的取值范围是 .
12.已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点可能有 个.
13.直线y=kx+6k交x轴于点A,交y轴于点B,以原点O为圆心,3为半径的⊙O与l相交,则k的取值范围为 .
14.如图,矩形ABCD中,AB=4,BC=6,E是边BC的中点,点P在边AD上,设DP=x,若以点D为圆心,DP为半径的⊙D与线段AE只有一个公共点,则所有满足条件的x的取值范围是 .
15.如图,坐标平面内,矩形AOCD的顶点A(0,2)、C(4,0)、D(4,2),抛物线y=x2﹣1经过点Q(a,4),P(b,4),⊙P的半径为1,当圆心P在抛物线上从点P运动到点Q,则在整个运动过程中,⊙P与矩形AOCD只有一个公共点的情况共出现 次.
三.解答题
16.如图,AB是⊙O的直径,AC与⊙O交于F,弦AD平分∠CAB,DE⊥AC,垂足为E.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径为3,若∠CAB=60°,求线段EF.
17.如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若AB=12,sinA=0.6,求△BDE的BE边上的高.
(3)在(2)的条件下,求cos∠BDE的值.
18.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
(1)试判断BD与⊙O的位置关系,并说明理由;
(2)当AB=BE=1时,求⊙O的面积;
(3)在(2)的条件下,求HG的长.
参考答案
一.选择题
1.解:∵⊙O的半径为10,圆心O到直线l的距离是13,而10<13,
∴点O到直线l的距离大于半径,
∴直线l与⊙O相离.
故选:A.
2.解:∵⊙O的半径为10,直线l与⊙O相交,
∴圆心到直线的距离小于圆的半径,
即d<10.
故选:A.
3.解:∵⊙O的直径为8cm,
∴r=4cm,
∵d=4cm,
∴d=r,
∴直线l与⊙O的位置关系是相切.
故选:B.
4.解:如右图所示,
当圆心从O1到O3的过程中,⊙O与三角形边的交点个数为3,当恰好到达O3时则变为4个交点,
作O3D⊥BC于点D,
则∠O3BD=∠ABC,
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
设O3A=a,则O3B=5﹣a,
∴,得a=,
∴当0<OA时,⊙O与三角形边的交点个数为3,
当点O为AB的中点时,⊙O与三角形边的交点个数为3,此时OA=2.5,
由上可得,0<OA或OA=2.5时,⊙O与三角形边的交点个数为3,
故选:B.
5.解:如图,
∵A(3,4),∴AO=5,
∵点A到直线y=﹣x的距离为AB的长小于圆的半径r,即AB<AO,
∴直线y=﹣x与⊙A的位置关系是相交,
故选:C.
6.解:∵⊙O1、⊙O2、⊙O3、⊙O4是四个半径为3的等圆,
∴圆心到直线l的距离为6是⊙O2,
故选:B.
7.解:∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=13.
分两种情况:
(1)圆与AB相切时,即r=CD=5×12÷13=;
(2)点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即5<r≤12.
故选:D.
8.解:如图,作CH⊥DA交DA的延长线于H.
∵S平行四边形ABCD=BC?CH,
∴CH==2,
∵2<5,
∴直线AD与⊙C相交,
故选:A.
9.解:作CD⊥AB于D,如图所示:
∵∠C=90°,AC=3,BC=4,
∴AB==5,
∵△ABC的面积=AB?CD=AC?BC,
∴CD===,
即圆心C到AB的距离d=,
∵AC<BC,
∴以C为圆心,r=或4为半径所作的圆与斜边AB只有一个公共点,
∴若⊙C与斜边AB有公共点,则r的取值范围是≤r≤4.
故选:D.
10.解:如图,
①当∠A为直角时,过点A作垂线与直线的交点W(﹣6,4),
②当∠B为直角时,过点B作垂线与直线的交点S(2,),
③若∠C为直角,
则点C在以线段AB为直径、AB中点E(﹣2,0)为圆心、4为半径的圆与直线的交点上.
在直线中,当x=0时y=2,即Q(0,2),
当y=0时x=6,即点P(6,0),
则PQ==4,
过AB中点E(﹣2,0),作EF⊥直线l于点F,
则∠EFP=∠QOP=90°,
∵∠EPF=∠QPO,
∴△EFP∽△QOP,
∴=,即=,
解得:EF=4,
∴以线段AB为直径、E(﹣2,0)为圆心的圆与直线恰好有一个交点.
所以直线上有一点C满足∠C=90°.
综上所述,使△ABC是直角三角形的点C的个数为3,
故选:C.
二.填空题
11.解:当直线y=﹣x+b与圆相切,且函数经过一、二、四象限时,如图.
在y=﹣x+b中,令x=0时,y=b,则与y轴的交点是(0,b),
当y=0时,x=b,则A的交点是(b,0),
则OA=OB,即△OAB是等腰直角三角形.
连接圆心O和切点C.则OC=1.
则OB=OC=.即b=;
同理,当直线y=﹣x+b与圆相切,且函数经过二、三、四象限时,b=﹣.
则若直线y=﹣x+b与⊙O相交,则b的取值范围是﹣≤b≤.
故答案为﹣≤b≤.
12.解:∵32+42=25,52=25,
∴三角形为直角三角形,
设内切圆半径为r,则(3+4+5)r=×3×4,
解得r=1,
所以应分为五种情况:
当一条边与圆相离时,有0个交点,
当一条边与圆相切时,有1个交点,
当一条边与圆相交时,有2个交点,
当圆与三角形内切圆时,有3个交点,
当两条边与圆同时相交时,有4个交点,
故公共点个数可能为0或1或2或3或4个.
故答案为0或1或2或3或4.
13.解:∵直线y=kx+6k交x轴于点A,交y轴于点B,
∴A(﹣6,0),B(0,6k),
设⊙O与AB相切于C,
连接OC,
∴OA=6,OC=3,∠ACO=90°,
∴OC=OA,
∴∠OAC=30°,
当⊙O与l相交时,OB=|6k|>2,
∴﹣<k<,
故答案为﹣<k<.
14.解:如图,当⊙D与AE相切时,设切点为G,连接DG,
∵PD=DG=x,
∵∠DAG=∠AEB,∠AGD=∠B=90°,
∴△AGD∽△EBA,
∴=,
∴=,
x=,
当⊙D过点E时,如图,⊙D与线段有两个公共点,连接DE,此时PD=DE=5,
∴当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,x满足的条件:x=或5<x≤6;
故答案为:x=或5<x≤6.
15.解:由题意抛物线y=x2﹣1与x轴的交点为(﹣1,0),(1,0),与y轴的交点为(0,﹣1).
观察图形可知当⊙P在AD上方与AD相切时,⊙P与矩形AOCD只有一个公共点,
当点P运动到(0,﹣1)时,⊙P与矩形AOCD只有一个公共点,
当点P运动到(﹣1,0)时,⊙P与矩形AOCD只有一个公共点,
∵OA=2,
∴⊙P在AD与OC中间时,不存在满足条件的⊙P,
综上所述,⊙P与矩形AOCD只有一个公共点的情况有3种情形,
故答案为3.
三.解答题
16.解:(1)直线DE与⊙O相切,理由如下:
连结OD.
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)过O作OG⊥AF于G,
∴AF=2AG,
∵∠BAC=60°,OA=3,
∴AG=OA=,
∴AF=3,
∴AF=OD,
∴四边形AODF是菱形,
∴DF∥OA,DF=OA=3,
∴∠EFD=∠BAC=60°,
∴EF=DF=.
17.解:(1)BD与⊙O相切,理由如下:
∵OA=OB,DB=DE,
∴∠A=∠OBA,∠DEB=∠DBE.
∵EC⊥OA,∠DEB=∠AEC,
∴∠A+∠DEB=90°,
∴∠OBA+∠DEB=90°,
∴∠OBD=90°.
∵OB是⊙O的半径,
∴BD与⊙O相切;
(2)过点D作DF⊥AB于点F,连接OE,如图:
∵点E是AB的中点,AB=12,
∴AE=EB=6,OE⊥AB.
又∵DF⊥AB,EC⊥OA,
∴∠EDF=∠A,
∵sinA=0.6,
∴sin∠EDF=0.6,
∵DB=DE,DF⊥AB,
∴EF==3,
∵sin∠EDF=,
∴=0.6,
∴ED=DB=5.
∴由勾股定理得:DF==4.
∴△BDE的BE边上的高为4.
(3)过点E作EH⊥DB于点H,
则S△EBD==,
∵EB=6,DF=4,DB=5,
∴EH=.
由勾股定理得:DH==,
∴cos∠BDE==.
18.解:(1)BD与⊙O相切,
理由:如图1,连接OB,
∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,∠EBF=90°,
∴∠C=∠DBC,EF为直径,
∴点O在EF上,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,
∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切;
(2)如图2,连接CF,HE,
∵∠CDE=90°,∠ABC=90°,
∴∠DEC=∠A,
∵∠CED=∠FEB,
∴∠FEB=∠A.
∵AB=BE,∠ABC=∠CBF=90°,
∴△ABC≌△EBF(ASA),
∵BC=BF,
∴CF=BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF=BF,
∴BF=+1,
∴EF==,
∵∠CBF=90°,
∴EF是⊙O的直径,
∴⊙O的面积=(EF)2?π=π=π;
(3)∵AB=BE,∠ABE=90°,
∴∠AEB=45°,
∵EA=EC,
∴∠C=22.5°,
∴∠H=∠BEG=∠CED=90°﹣22.5°=67.5°,
∵BH平分∠CBF,
∴∠EBG=∠HBF=45°,
∴∠BGE=∠BFH=67.5°,
∴BG=BE=1,BH=BF=1+,
∴HG=BH﹣BG=.
