人教版数学七年级下册 第5章 5.3 平行线的性质 同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第5章 5.3 平行线的性质 同步测试试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 156.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 18:55:32 | ||
图片预览




文档简介
平行线的性质同步测试试题(一)
一.选择题
1.判断命题“如果n<1,那么n2﹣2<0”是假命题,只需举出一个反例.反例中的n可以为( )
A. B.0 C.﹣1 D.﹣2
2.下列命题:①有理数与数轴上的点一一对应;②过一点有且只有一条直线与已知直线平行;③从直线外一点到这条直线的垂线段叫做点到直线的距离;④负数没有平方根.其中是真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图,若直线l1∥l2,则下列各式成立的是( )
A.∠1=∠2 B.∠4=∠5 C.∠2+∠5=180° D.∠1+∠3=180°
4.下列命题是真命题的是( )
A.对边相等的四边形是平行四边形
B.有一个角是90°的平行四边形是矩形
C.邻边相等的四边形是菱形
D.对角线互相垂直的平行四边形为正方形
5.在同一平面内,不重合的三条直线a、b、c中,如果a⊥b,b⊥c,那么a与c的位置关系是( )
A.垂直 B.平行 C.相交 D.不能确定
6.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等 B.互余或互补 C.互补 D.相等或互补
7.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
8.下列说法正确的是( )
①在同一平面内,过一点有且只有一条直线与已知直线垂直;
②在同一平面内,过一点有且只有一条直线与已知直线平行;
③P是直线a外一点,A、B、C分别是直线a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1;
④相等的角是对顶角;
⑤同旁内角互补.
A.1个 B.2个 C.3个 D.4个
9.如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
A.30° B.40° C.50° D.60°
10.如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5,且A3A4∥B3B4,直线l经过点B2,B3.则下列结论错误的是( )
A.∠A1A2A3=120°
B.∠A2A3A4=120°
C.∠B2B3B4=108°
D.直线l与A1A2的夹角α=50°
二.填空题
11.在同一平面内,∠A与∠B的两边分别平行,若∠A=50°,则∠B的度数为 °.
12.下列四个命题中:
①对顶角相等;②如果两条直线被第三条直线所截,那么同位角相等;③如果两个实数的平方相等,那么这两个实数也相等;④当m≠0时,点P(m2,﹣m)在第四象限内.其中真命题有 (填序号).
13.如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
14.下列5个命题中:①对顶角相等;②同位角相等;③平行于同一条直线的两直线平行;④互补的角是邻补角;⑤经过直线外一点,有且只有一条直线与已知直线平行;真命题共有 个.
15.如图,BD平分∠ABC,EF∥BC,AE与BD交于点G,连接ED.若∠A=22°,∠D=20°,∠DEF=2∠AED,则∠AGB的大小= (度).
三.解答题
16.如图,点D、E、F分别是△ABC三边上的点,DF∥AC,∠BFD=∠CED,请写出∠B与∠CDE之间的数量关系,并说明理由.
17.如图,已知∠1、∠2互为补角,且∠3=∠B.
(1)求证:∠AFE=∠C;
(2)若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE的度数.
18.如图,点D为线段BC上的一点,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,那么AD平分∠BAC吗?请说明理由.
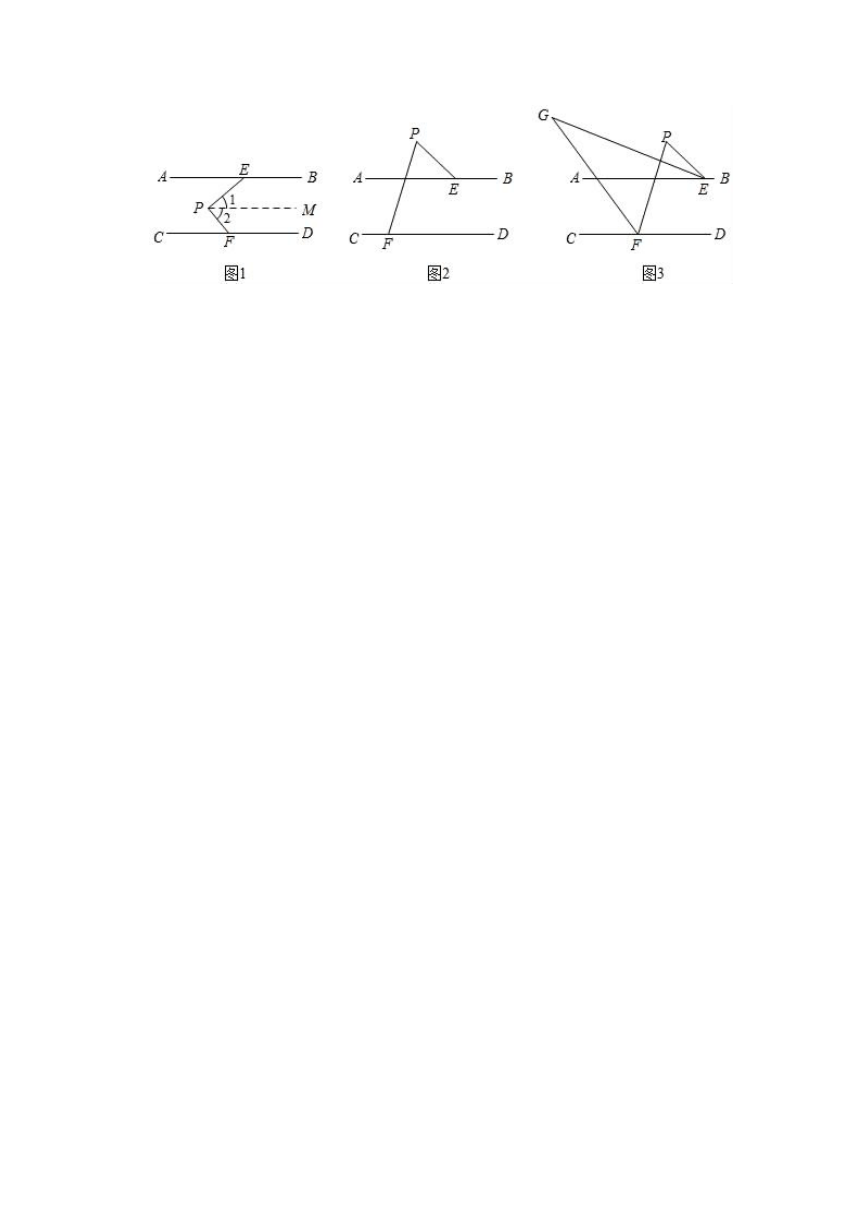
19.,请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°( )
∵AB∥CD,(已知)
∴PM∥CD,( )
∴∠2+∠PFD=180°.如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;
(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是 .(直接写出答案,不需要写出过程)
参考答案与试题解析
一.选择题
1.【解答】解:﹣2<1,
(﹣2)2﹣2>0,
∴当n=﹣2时,“如果n<1,那么n2﹣2<0”是假命题,
故选:D.
2.【解答】解:①实数与数轴上的点一一对应,则本小题说法错误;
②过直线外一点有且只有一条直线与已知直线平行,则本小题说法错误;
③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,则本小题说法错误;
④负数没有平方根,则本小题说法正确;
故选:A.
3.【解答】解:∵直线l1∥l2,
∴∠1+∠3=180°,∠2+∠4=180°,
故选:D.
4.【解答】解:A、两组对边分别相等的四边形是平行四边形,原命题是假命题,不符合题意;
B、有一个角是90°的平行四边形是矩形,是真命题,符合题意;
C、邻边相等的平行四边形是菱形,原命题是假命题,不符合题意;
D、对角线互相相等且垂直的平行四边形为正方形,原命题是假命题,不符合题意;
故选:B.
5.【解答】解:∵同一平面内的三条直线a,b,c,a⊥b,b⊥c,
∴a∥c,
故选:B.
6.【解答】解:如图知∠A和∠B的关系是相等或互补.
故选:D.
7.【解答】解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
8.【解答】解:①在同一平面内,过一点有且只有一条直线与已知直线垂直,是真命题;
②在同一平面内,过直线外一点有且只有一条直线与已知直线平行,原命题是假命题;
③P是直线a外一点,A、B、C分别是直线a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定不大于1,原命题是假命题;
④相等的角不一定是对顶角,原命题是假命题;
⑤两直线平行,同旁内角互补,原命题是假命题;
故选:A.
9.【解答】解:∵直角三角板的直角顶点在直线a上,∠1=30°,
∴∠3=60°,
∵a∥b,
∴∠2=∠3=60°,
故选:D.
10.【解答】解:设l交A1A2于E、交A4A3于D,如图所示:
∵六边形A1A2A3A4A5A6是正六边形,六边形的内角和=(6﹣2)×180°=720°,
∴∠A1A2A3=∠A2A3A4==120°,故A、B正确,
∵五边形B1B2B3B4B5是正五边形,五边形的内角和=(5﹣2)×180°=540°,
∴∠B2B3B4==108°,故C正确,
∴∠B4B3D=180°﹣108°=72°,
∵A3A4∥B3B4,
∴∠EDA3=∠B4B3D=72°,
∴α=∠A2ED=360°﹣∠A1A2A3﹣∠A2A3A4﹣∠EDA3=360°﹣120°﹣120°﹣72°=48°,故D错误;
故选:D.
二.填空题(共5小题)
11.【解答】解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=50°,
∴∠B=50°,或∠B=180°﹣∠A=180°﹣50°=130°.
故答案为:50或130.
12.【解答】解:①对顶角相等,本小题说法是真命题;
②如果两条平行线被第三条直线所截,那么同位角相等,本小题说法是假命题;
③如果两个实数的平方相等,那么这两个实数相等或互为相反数,本小题说法是假命题;
④当m≠0时,点P(m2,﹣m)在第四象限内或第一象限内,本小题说法是假命题;
故答案为:①.
13.【解答】解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
14.【解答】解:对顶角相等,所以①为真命题;
两直线平行,同位角相等,所以②为假命题;
平行于同一条直线的两直线平行,所以③为真命题;
有一条公共边且互补的角是邻补角,所以④为假命题;
经过直线外一点,有且只有一条直线与已知直线平行,所以⑤为真命题.
故答案为3.
15.【解答】解:∵BD平分∠ABC,
∴∠ABD=∠DBC,
设∠ABD=x°,DE与BC交于点M,
∵∠AGB=∠DGE,
∵∠AGB=180°﹣∠A﹣∠ABD,∠DGE=180°﹣∠D﹣∠AED,
∴∠AED=x+22°,
∵∠DGF=2∠AED,
∴∠DEF=2x+44°,
∵BC∥EF,
∴∠DMC=∠DEF=2x+44°,
∵∠DMC=∠D+∠DBC,
∴2x+44°=x+22°,
解得:x=16°,
∴∠AGB=180°﹣∠A﹣∠ABD=180°﹣22°﹣16°=142°,
故答案为:142.
三.解答题(共4小题)
16.【解答】解:∠B=∠CDE,
理由:∵DF∥AC,
∴∠DFB=∠A,
∵∠BFD=∠CED,
∴∠A=∠CED,
∴AB∥DE,
∴∠B=∠CDE.
17.【解答】证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=85°,∠3=50°,
∴∠FED=85°﹣50°=35°,
∵EF∥BC,
∴∠BCE=∠FED=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∴∠AFE=∠ACB=70°.
18.【解答】解:(1)AD∥EF,
理由:∵∠BDA+∠CEG=180°,∠BDA+∠CDA=180°,
∴∠CEG=∠CDA,
∴AD∥EF;
(2)AD平分∠BAC,
理由:∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠EGC,
∵∠F=∠H,
∴∠F=∠EGC,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠EGC,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
19.【解答】解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°. (两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
故答案为:两直线平行,内错角相等;平行于同一条直线的两直线平行;两直线平行,同旁内角互补;
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)令AB与PF交点为O,连接EF,如图3.
在△GFE中,∠G=180°﹣(∠GFE+∠GEF),
∵∠GEF=PEA+∠OEF,∠GFE=PFC+∠OFE,
∴∠GEF+∠GFE=PEA+∠OEF+PFC+∠OFE,
∵由(2)知∠PFC=∠PEA+∠P,
∴∠PEA=∠PFC﹣α,
∵∠OFE+∠OEF=180°﹣∠FOE=180°﹣∠PFC,
∴∠GEF+∠GFE=(∠PFC﹣α)+∠PFC+180°﹣∠PFC=180°﹣α,
∴∠G=180°﹣(∠GEF+∠GFE)=180°﹣180°+α=α.
故答案为:α.
一.选择题
1.判断命题“如果n<1,那么n2﹣2<0”是假命题,只需举出一个反例.反例中的n可以为( )
A. B.0 C.﹣1 D.﹣2
2.下列命题:①有理数与数轴上的点一一对应;②过一点有且只有一条直线与已知直线平行;③从直线外一点到这条直线的垂线段叫做点到直线的距离;④负数没有平方根.其中是真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图,若直线l1∥l2,则下列各式成立的是( )
A.∠1=∠2 B.∠4=∠5 C.∠2+∠5=180° D.∠1+∠3=180°
4.下列命题是真命题的是( )
A.对边相等的四边形是平行四边形
B.有一个角是90°的平行四边形是矩形
C.邻边相等的四边形是菱形
D.对角线互相垂直的平行四边形为正方形
5.在同一平面内,不重合的三条直线a、b、c中,如果a⊥b,b⊥c,那么a与c的位置关系是( )
A.垂直 B.平行 C.相交 D.不能确定
6.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等 B.互余或互补 C.互补 D.相等或互补
7.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c D.∵∠2+∠3=180°,∴a∥c
8.下列说法正确的是( )
①在同一平面内,过一点有且只有一条直线与已知直线垂直;
②在同一平面内,过一点有且只有一条直线与已知直线平行;
③P是直线a外一点,A、B、C分别是直线a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1;
④相等的角是对顶角;
⑤同旁内角互补.
A.1个 B.2个 C.3个 D.4个
9.如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
A.30° B.40° C.50° D.60°
10.如图,正六边形A1A2A3A4A5A6内部有一个正五边形B1B2B3B4B5,且A3A4∥B3B4,直线l经过点B2,B3.则下列结论错误的是( )
A.∠A1A2A3=120°
B.∠A2A3A4=120°
C.∠B2B3B4=108°
D.直线l与A1A2的夹角α=50°
二.填空题
11.在同一平面内,∠A与∠B的两边分别平行,若∠A=50°,则∠B的度数为 °.
12.下列四个命题中:
①对顶角相等;②如果两条直线被第三条直线所截,那么同位角相等;③如果两个实数的平方相等,那么这两个实数也相等;④当m≠0时,点P(m2,﹣m)在第四象限内.其中真命题有 (填序号).
13.如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
14.下列5个命题中:①对顶角相等;②同位角相等;③平行于同一条直线的两直线平行;④互补的角是邻补角;⑤经过直线外一点,有且只有一条直线与已知直线平行;真命题共有 个.
15.如图,BD平分∠ABC,EF∥BC,AE与BD交于点G,连接ED.若∠A=22°,∠D=20°,∠DEF=2∠AED,则∠AGB的大小= (度).
三.解答题
16.如图,点D、E、F分别是△ABC三边上的点,DF∥AC,∠BFD=∠CED,请写出∠B与∠CDE之间的数量关系,并说明理由.
17.如图,已知∠1、∠2互为补角,且∠3=∠B.
(1)求证:∠AFE=∠C;
(2)若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE的度数.
18.如图,点D为线段BC上的一点,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,那么AD平分∠BAC吗?请说明理由.
19.,请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°( )
∵AB∥CD,(已知)
∴PM∥CD,( )
∴∠2+∠PFD=180°.如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;
(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是 .(直接写出答案,不需要写出过程)
参考答案与试题解析
一.选择题
1.【解答】解:﹣2<1,
(﹣2)2﹣2>0,
∴当n=﹣2时,“如果n<1,那么n2﹣2<0”是假命题,
故选:D.
2.【解答】解:①实数与数轴上的点一一对应,则本小题说法错误;
②过直线外一点有且只有一条直线与已知直线平行,则本小题说法错误;
③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,则本小题说法错误;
④负数没有平方根,则本小题说法正确;
故选:A.
3.【解答】解:∵直线l1∥l2,
∴∠1+∠3=180°,∠2+∠4=180°,
故选:D.
4.【解答】解:A、两组对边分别相等的四边形是平行四边形,原命题是假命题,不符合题意;
B、有一个角是90°的平行四边形是矩形,是真命题,符合题意;
C、邻边相等的平行四边形是菱形,原命题是假命题,不符合题意;
D、对角线互相相等且垂直的平行四边形为正方形,原命题是假命题,不符合题意;
故选:B.
5.【解答】解:∵同一平面内的三条直线a,b,c,a⊥b,b⊥c,
∴a∥c,
故选:B.
6.【解答】解:如图知∠A和∠B的关系是相等或互补.
故选:D.
7.【解答】解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
8.【解答】解:①在同一平面内,过一点有且只有一条直线与已知直线垂直,是真命题;
②在同一平面内,过直线外一点有且只有一条直线与已知直线平行,原命题是假命题;
③P是直线a外一点,A、B、C分别是直线a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定不大于1,原命题是假命题;
④相等的角不一定是对顶角,原命题是假命题;
⑤两直线平行,同旁内角互补,原命题是假命题;
故选:A.
9.【解答】解:∵直角三角板的直角顶点在直线a上,∠1=30°,
∴∠3=60°,
∵a∥b,
∴∠2=∠3=60°,
故选:D.
10.【解答】解:设l交A1A2于E、交A4A3于D,如图所示:
∵六边形A1A2A3A4A5A6是正六边形,六边形的内角和=(6﹣2)×180°=720°,
∴∠A1A2A3=∠A2A3A4==120°,故A、B正确,
∵五边形B1B2B3B4B5是正五边形,五边形的内角和=(5﹣2)×180°=540°,
∴∠B2B3B4==108°,故C正确,
∴∠B4B3D=180°﹣108°=72°,
∵A3A4∥B3B4,
∴∠EDA3=∠B4B3D=72°,
∴α=∠A2ED=360°﹣∠A1A2A3﹣∠A2A3A4﹣∠EDA3=360°﹣120°﹣120°﹣72°=48°,故D错误;
故选:D.
二.填空题(共5小题)
11.【解答】解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=50°,
∴∠B=50°,或∠B=180°﹣∠A=180°﹣50°=130°.
故答案为:50或130.
12.【解答】解:①对顶角相等,本小题说法是真命题;
②如果两条平行线被第三条直线所截,那么同位角相等,本小题说法是假命题;
③如果两个实数的平方相等,那么这两个实数相等或互为相反数,本小题说法是假命题;
④当m≠0时,点P(m2,﹣m)在第四象限内或第一象限内,本小题说法是假命题;
故答案为:①.
13.【解答】解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
14.【解答】解:对顶角相等,所以①为真命题;
两直线平行,同位角相等,所以②为假命题;
平行于同一条直线的两直线平行,所以③为真命题;
有一条公共边且互补的角是邻补角,所以④为假命题;
经过直线外一点,有且只有一条直线与已知直线平行,所以⑤为真命题.
故答案为3.
15.【解答】解:∵BD平分∠ABC,
∴∠ABD=∠DBC,
设∠ABD=x°,DE与BC交于点M,
∵∠AGB=∠DGE,
∵∠AGB=180°﹣∠A﹣∠ABD,∠DGE=180°﹣∠D﹣∠AED,
∴∠AED=x+22°,
∵∠DGF=2∠AED,
∴∠DEF=2x+44°,
∵BC∥EF,
∴∠DMC=∠DEF=2x+44°,
∵∠DMC=∠D+∠DBC,
∴2x+44°=x+22°,
解得:x=16°,
∴∠AGB=180°﹣∠A﹣∠ABD=180°﹣22°﹣16°=142°,
故答案为:142.
三.解答题(共4小题)
16.【解答】解:∠B=∠CDE,
理由:∵DF∥AC,
∴∠DFB=∠A,
∵∠BFD=∠CED,
∴∠A=∠CED,
∴AB∥DE,
∴∠B=∠CDE.
17.【解答】证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=85°,∠3=50°,
∴∠FED=85°﹣50°=35°,
∵EF∥BC,
∴∠BCE=∠FED=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∴∠AFE=∠ACB=70°.
18.【解答】解:(1)AD∥EF,
理由:∵∠BDA+∠CEG=180°,∠BDA+∠CDA=180°,
∴∠CEG=∠CDA,
∴AD∥EF;
(2)AD平分∠BAC,
理由:∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠EGC,
∵∠F=∠H,
∴∠F=∠EGC,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠EGC,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
19.【解答】解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°. (两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
故答案为:两直线平行,内错角相等;平行于同一条直线的两直线平行;两直线平行,同旁内角互补;
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)令AB与PF交点为O,连接EF,如图3.
在△GFE中,∠G=180°﹣(∠GFE+∠GEF),
∵∠GEF=PEA+∠OEF,∠GFE=PFC+∠OFE,
∴∠GEF+∠GFE=PEA+∠OEF+PFC+∠OFE,
∵由(2)知∠PFC=∠PEA+∠P,
∴∠PEA=∠PFC﹣α,
∵∠OFE+∠OEF=180°﹣∠FOE=180°﹣∠PFC,
∴∠GEF+∠GFE=(∠PFC﹣α)+∠PFC+180°﹣∠PFC=180°﹣α,
∴∠G=180°﹣(∠GEF+∠GFE)=180°﹣180°+α=α.
故答案为:α.
