北师大版九年级数学下册 第三章 圆 单元检测试题 (word版,含答案)
文档属性
| 名称 | 北师大版九年级数学下册 第三章 圆 单元检测试题 (word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 306.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 22:08:04 | ||
图片预览

文档简介
第三章
圆
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列说法正确的个数是(
)
①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.
A.
B.
C.
D.
?
2.
圆内接四边形中,、、的度数比是,则的度数为(
)
A.
B.
C.
D.
?
?
3.
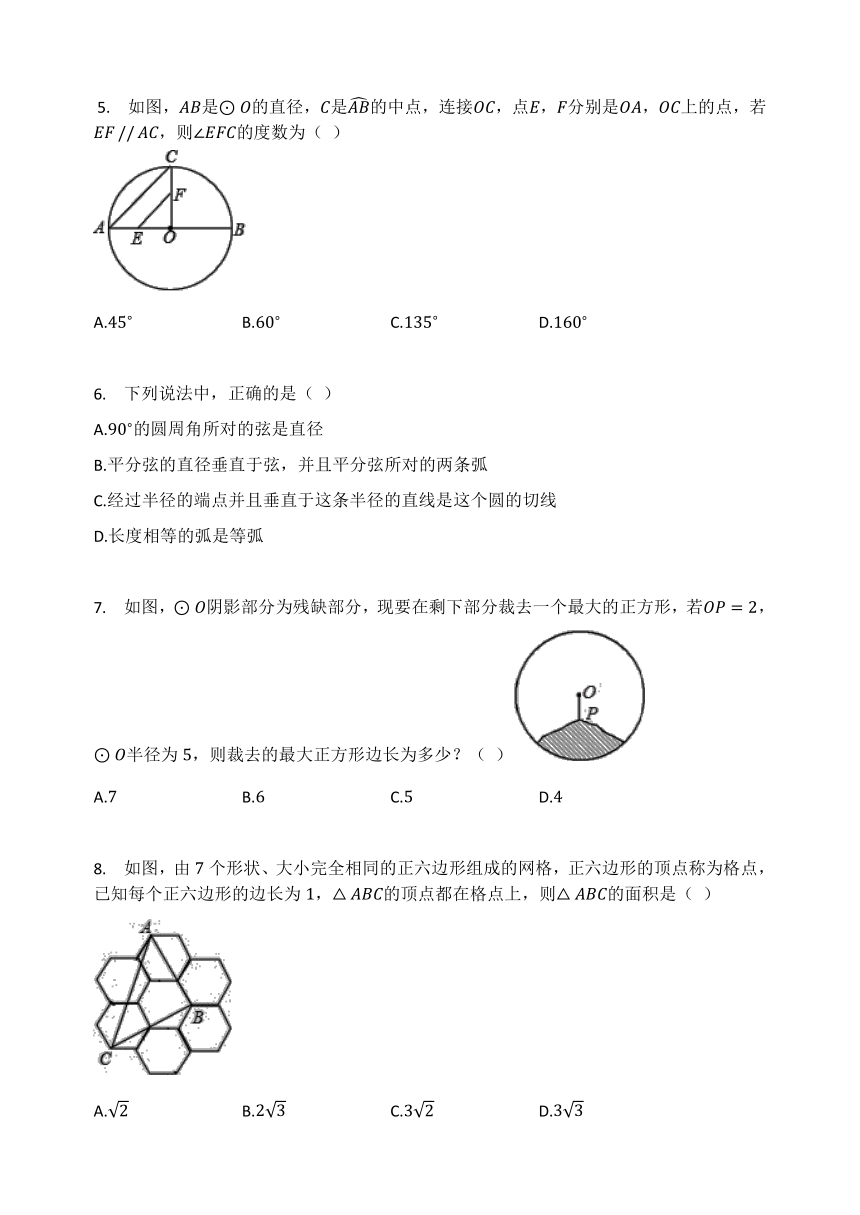
某公园计划砌一个形状如图的喷水池,后来有人建议改为图的形状,且外圆的直径不变,若两种方案砌各圆形水池的周边需用的材料费分别为和,则(
)
A.
B.
C.
D.无法确定
?
4.
如图,、是的两条弦,于,于.如果,那么下列判断中错误的是(
)
A.
B.
C.
D.
?5.
如图,是的直径,是的中点,连接,点,分别是,上的点,若,则的度数为(
)
A.
B.
C.
D.
?
6.
下列说法中,正确的是(
)
A.的圆周角所对的弦是直径
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.经过半径的端点并且垂直于这条半径的直线是这个圆的切线
D.长度相等的弧是等弧
?
7.
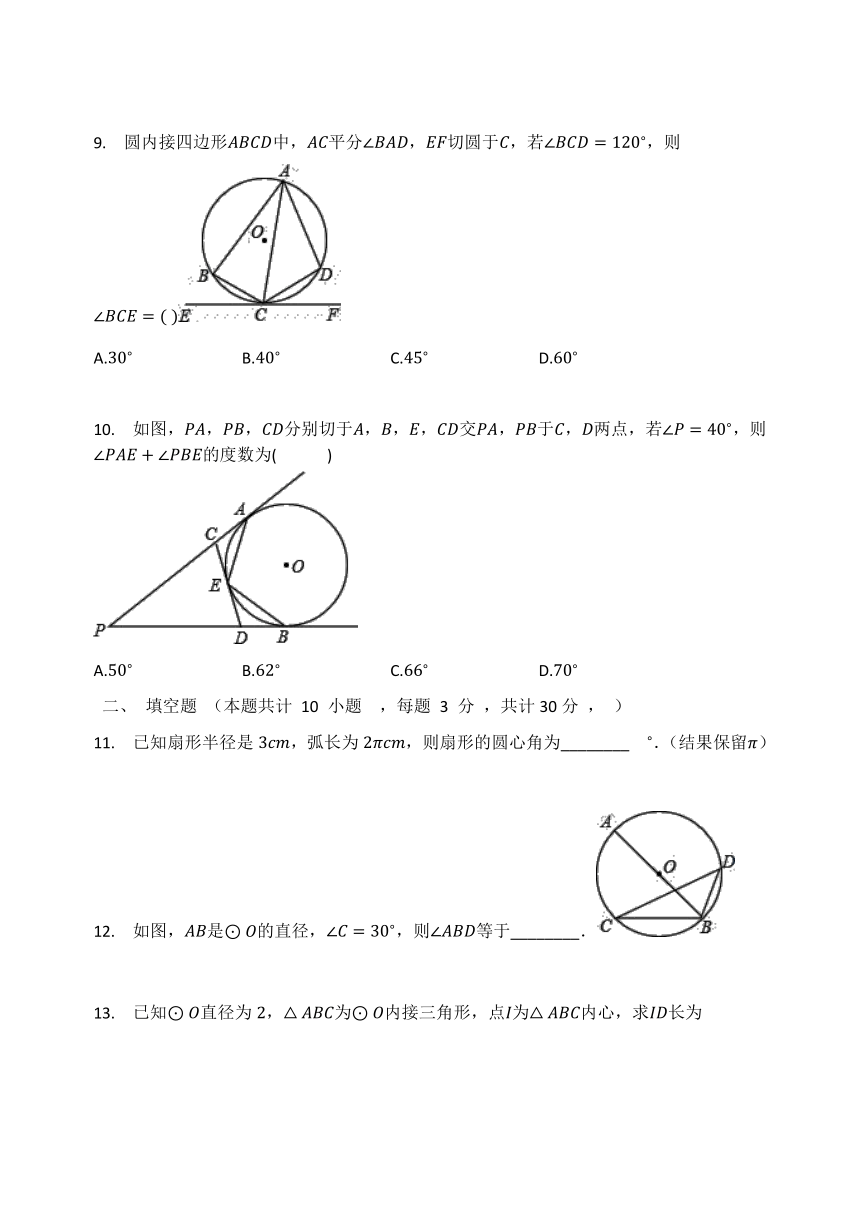
如图,阴影部分为残缺部分,现要在剩下部分裁去一个最大的正方形,若,半径为,则裁去的最大正方形边长为多少?(
)
A.
B.
C.
D.
?
8.
如图,由个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为,的顶点都在格点上,则的面积是(
)
A.
B.
C.
D.
?
9.
圆内接四边形中,平分,切圆于,若,则
A.
B.
C.
D.
?
10.
如图,,,分别切于,,,交,于,两点,若,则的度数为(?
?
?
?
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知扇形半径是,弧长为,则扇形的圆心角为________.(结果保留)
?
12.
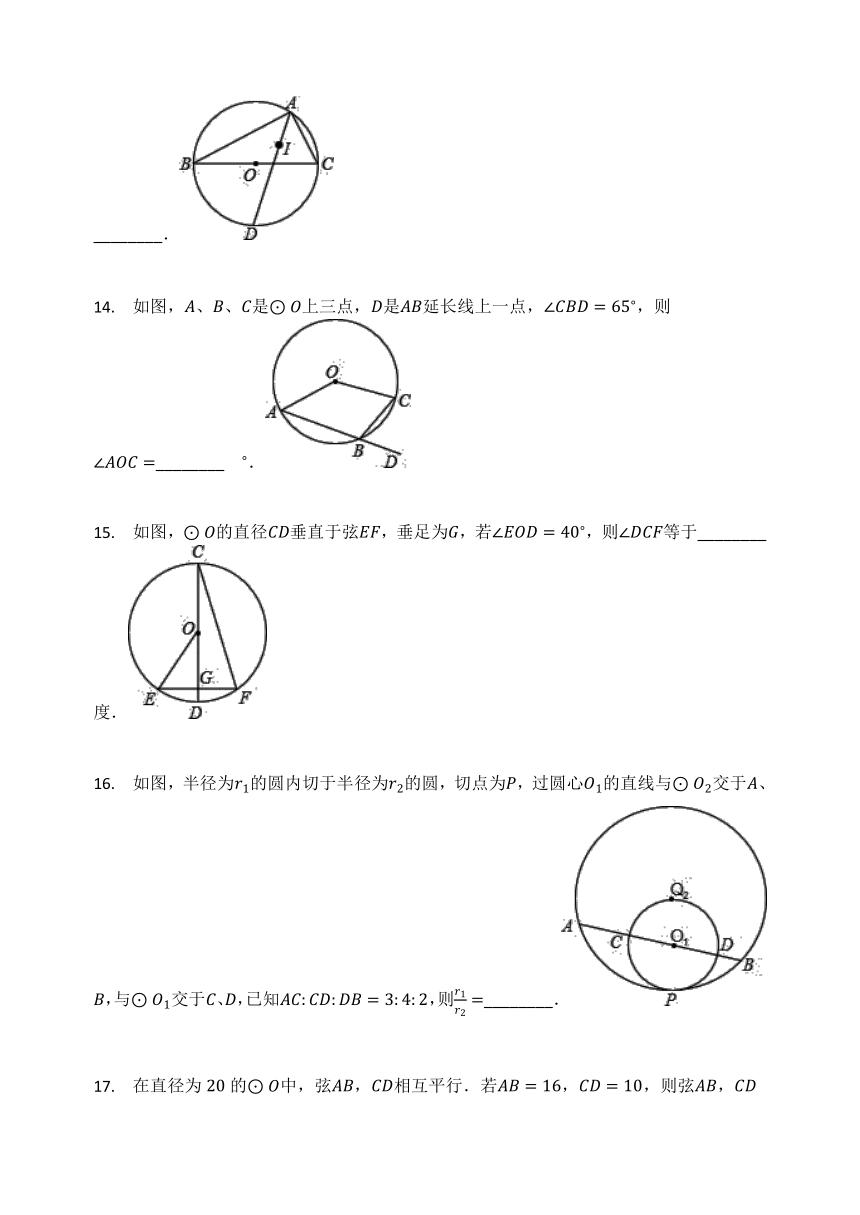
如图,是的直径,,则等于________.
?
13.
已知直径为,为内接三角形,点为内心,求长为________.
?
14.
如图,、、是上三点,是延长线上一点,,则________.
?
15.
如图,的直径垂直于弦,垂足为,若,则等于________度.
?
16.
如图,半径为的圆内切于半径为的圆,切点为,过圆心的直线与交于、,与交于、,已知,则________.
?
17.
在直径为的中,弦,相互平行.若,,则弦,之间的距离是________.
?
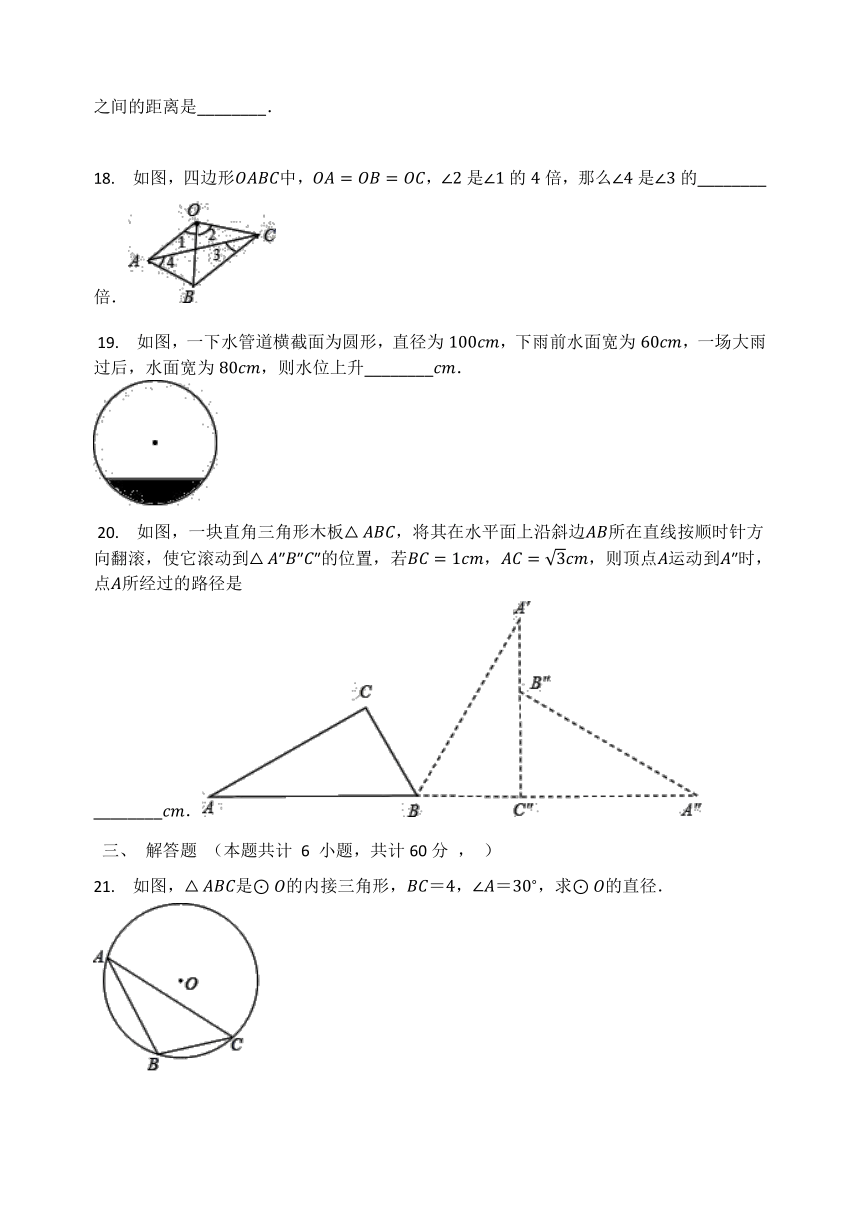
18.
如图,四边形中,,是的倍,那么是的________倍.
?19.
如图,一下水管道横截面为圆形,直径为,下雨前水面宽为,一场大雨过后,水面宽为,则水位上升________.
?20.
如图,一块直角三角形木板,将其在水平面上沿斜边所在直线按顺时针方向翻滚,使它滚动到″″″的位置,若,,则顶点运动到″时,点所经过的路径是________.
三、
解答题
(本题共计
6
小题,共计60分
,
)
21.
如图,是的内接三角形,=,=,求的直径.
?
22.
如图,已知是的直径,与相交于点,,,求的度数.
?
23.
如图,已知为的直径,,,求的度数.
?
24.
如图,已知、分别是的内角与外角的平分线,、分别与的外接圆交于点、.求证:
(1)是的外接圆的直径;
(2)是的垂直平分线.
?
25.
如图,四边形内接于,,过作垂足为,且.
(1)求证:是的切线;
(2)若,,求的值.
?26.
如图,是的直径,,于点,交于点,交的延长线于点,.
(1)求证:;
(2)求证:是的切线;
(3)若,,求的长.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:直径所在的直线是圆的对称轴,所以①错误;
半径相等的两个半圆是等弧,所以②正确;
能完全重合的两条弧是等弧,所以③错误;
和圆有唯一公共点的直线是圆的切线,所以④错误.
故选.
2.
【答案】
B
3.
【答案】
C
【解答】
解:在图中,,
在图中,,
所以,即两种方案各圆形水池的周边需要的材料一样多.
故选.
4.
【答案】
D
【解答】
解:、∵
,
∴
,
故本选项正确;
、∵
,
∴
,
故本选项正确;
、∵
,,,
∴
,,
∵
,
∴
,
∴
,
故本选项正确;
、不一定等于,
故本选项错误;
故选.
5.
【答案】
C
【解答】
∵
是的直径,是的中点,
∴
,
∵
,
∴
是等腰直角三角形,
∴
,
∵
,
∴
,
∴
,
6.
【答案】
A
【解答】
解:、根据圆周角定理得:的圆周角所对的弦是直径,故本选项正确;
、
如图,符合条件,当和不垂直,故本选项错误;
、
如图,,过半径端点,但是不是圆的切线,故本选项错误;
、如图,
弧和弧长度相等,但是弧和弧不是等弧,故本选项错误;
故选.
7.
【答案】
B
【解答】
解:如图:正方形是最大的正方形,,
延长交于点,
∴
,,,
∵
,半径为,
可设正方形的边长为,
则,,
∴
在直角中,,
解得;
即正方形的边长为.
故选.
8.
【答案】
D
【解答】
解:延长,然后作出过点与格点所在的直线,一定交于格点.如图所示:
正六边形的边长为,则半径是,则,
两平行的边之间距离是:,
则的边上的高是:,
边上的高是:,
则.
故选:.
9.
【答案】
A
【解答】
解:∵
四边形内接于,
∴
,
∴
,
∵
平分,
∴
,
∵
切于,
∴
.故选.
10.
【答案】
D
【解答】
解:∵
,,分别切于,,,交,于,两点,
∴
,,
∴
,,
∴
,
,
∴
,,
即,,
∵
,
∴
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:设扇形的圆心角为,
∵
扇形半径是,弧长为,
∴
,
解得:,
故答案为:.
12.
【答案】
【解答】
解:连接,
∵
是的直径,
∴
,
∵
,
∴
.
故答案为:.
13.
【答案】
【解答】
解:连结,,,,如图,
∵
点为内心,
∴
平分,平分,
∴
,,
∵
,
∴
,
∵
,
∴
,即,
∴
,
∵
为直径,
∴
,
∵
,
∴
,
∴
,
∴
为等腰直角三角形,
∴
,
∴
.
故答案为.
14.
【答案】
【解答】
解:设点是优弧(不与,重合)上的一点,连接、,
∵
.
∴
.
∴
.
故答案是:.
15.
【答案】
【解答】
解:∵
的直径垂直于弦,
∴
弧弧,
∵
,
∴
弧的度数是,
∴
由圆周角定理得:,
故答案为:.
16.
【答案】
【解答】
解:设,,分别是,,,
则,
根据两圆相切,切点一定在连心线上,
则作直线,一定经过点,交圆于另一点,
根据相交弦定理,得,
则
∴
.
17.
【答案】
【解答】
解:过点作于,交于,连接、,如图,
∵
,
∴
,
∴
,,
在中,,
在中,,
当点在和之间时,,
当点不在和之间时,,
∴
、之间的距离为.
故答案为.
18.
【答案】
【解答】
解:∵
四边形中,,
∴
、、在以为圆心,以为半径的圆上;(如图)
∵
,,,
∴
;
故是的倍.
19.
【答案】
或
【解答】
解:作半径于,连接.
由垂径定理得:,
在中,,
当水位上升到圆心以下时??水面宽时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为或.
故答案为:或.
20.
【答案】
【解答】
解:,,
∴
,,.
∴
点运动的第一段弧长.
第二段弧长.
∴
顶点运动到″时,点所经过的路径.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
连接,,
∵
=,
∴
=,
∵
=,
∴
是等边三角形,
∴
==,
∴
的直径=.
【解答】
连接,,
∵
=,
∴
=,
∵
=,
∴
是等边三角形,
∴
==,
∴
的直径=.
22.
【答案】
解:连接,
∵
是直径,
∴
(直径所对的角为),
∴
,
∵
弧所对的圆周角是和,
∴
(在同圆中,同弧所对的圆周角相等),
在中,,,
∴
,
∴
,
∴
.
【解答】
解:连接,
∵
是直径,
∴
(直径所对的角为),
∴
,
∵
弧所对的圆周角是和,
∴
(在同圆中,同弧所对的圆周角相等),
在中,,,
∴
,
∴
,
∴
.
23.
【答案】
解:连接,
∵
和都为所对的圆周角,
∴
,
∵
为的直径,
∴
,
∴
,
∵
,
∴
,
∵
,,
∴
,
∴
.
【解答】
解:连接,
∵
和都为所对的圆周角,
∴
,
∵
为的直径,
∴
,
∴
,
∵
,
∴
,
∵
,,
∴
,
∴
.
24.
【答案】
证明:(1)∵
、分别是的内角与外角的平分线,
∴
,,
∴
,
即,
∴
是的外接圆的直径;
(2)∵
是的平分线,
∴
,
∴
,又是的外接圆的直径,
∴
是的垂直平分线.
【解答】
证明:(1)∵
、分别是的内角与外角的平分线,
∴
,,
∴
,
即,
∴
是的外接圆的直径;
(2)∵
是的平分线,
∴
,
∴
,又是的外接圆的直径,
∴
是的垂直平分线.
25.
【答案】
证明:∵
,
∴
为直径,
∴
,
∵
,
∴
,
∵
,,
∴
,
∵
,
∴
,
∴
,即,
∴
,
∴
是的切线;
过点作,垂足为,如图,则,
∴
,
易证得四边形为矩形,
∴
,
∵
,
∴
,
在中,,
∵
,
∴
,
∴
,即,
∴
.
【解答】
证明:∵
,
∴
为直径,
∴
,
∵
,
∴
,
∵
,,
∴
,
∵
,
∴
,
∴
,即,
∴
,
∴
是的切线;
过点作,垂足为,如图,则,
∴
,
易证得四边形为矩形,
∴
,
∵
,
∴
,
在中,,
∵
,
∴
,
∴
,即,
∴
.
26.
【答案】
(1)证明:∵
,
∴
,
∵
是的直径,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
,
∴
;
(2)证明:如解图,连结,
∵
,
∴
,
由(1)可知,
∵
,
∴
,
∵
,
∴
,
∴
,
∴
,
又∵
为的半径,
∴
是的切线;
(3)解:∵
,
∴
,
在中,
∵
,
,
∴
.
【解答】
(1)证明:∵
,
∴
,
∵
是的直径,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
,
∴
;
(2)证明:如解图,连结,
∵
,
∴
,
由(1)可知,
∵
,
∴
,
∵
,
∴
,
∴
,
∴
,
又∵
为的半径,
∴
是的切线;
(3)解:∵
,∴
,
在中,
∵
,
,
∴
.
圆
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列说法正确的个数是(
)
①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.
A.
B.
C.
D.
?
2.
圆内接四边形中,、、的度数比是,则的度数为(
)
A.
B.
C.
D.
?
?
3.
某公园计划砌一个形状如图的喷水池,后来有人建议改为图的形状,且外圆的直径不变,若两种方案砌各圆形水池的周边需用的材料费分别为和,则(
)
A.
B.
C.
D.无法确定
?
4.
如图,、是的两条弦,于,于.如果,那么下列判断中错误的是(
)
A.
B.
C.
D.
?5.
如图,是的直径,是的中点,连接,点,分别是,上的点,若,则的度数为(
)
A.
B.
C.
D.
?
6.
下列说法中,正确的是(
)
A.的圆周角所对的弦是直径
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.经过半径的端点并且垂直于这条半径的直线是这个圆的切线
D.长度相等的弧是等弧
?
7.
如图,阴影部分为残缺部分,现要在剩下部分裁去一个最大的正方形,若,半径为,则裁去的最大正方形边长为多少?(
)
A.
B.
C.
D.
?
8.
如图,由个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为,的顶点都在格点上,则的面积是(
)
A.
B.
C.
D.
?
9.
圆内接四边形中,平分,切圆于,若,则
A.
B.
C.
D.
?
10.
如图,,,分别切于,,,交,于,两点,若,则的度数为(?
?
?
?
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知扇形半径是,弧长为,则扇形的圆心角为________.(结果保留)
?
12.
如图,是的直径,,则等于________.
?
13.
已知直径为,为内接三角形,点为内心,求长为________.
?
14.
如图,、、是上三点,是延长线上一点,,则________.
?
15.
如图,的直径垂直于弦,垂足为,若,则等于________度.
?
16.
如图,半径为的圆内切于半径为的圆,切点为,过圆心的直线与交于、,与交于、,已知,则________.
?
17.
在直径为的中,弦,相互平行.若,,则弦,之间的距离是________.
?
18.
如图,四边形中,,是的倍,那么是的________倍.
?19.
如图,一下水管道横截面为圆形,直径为,下雨前水面宽为,一场大雨过后,水面宽为,则水位上升________.
?20.
如图,一块直角三角形木板,将其在水平面上沿斜边所在直线按顺时针方向翻滚,使它滚动到″″″的位置,若,,则顶点运动到″时,点所经过的路径是________.
三、
解答题
(本题共计
6
小题,共计60分
,
)
21.
如图,是的内接三角形,=,=,求的直径.
?
22.
如图,已知是的直径,与相交于点,,,求的度数.
?
23.
如图,已知为的直径,,,求的度数.
?
24.
如图,已知、分别是的内角与外角的平分线,、分别与的外接圆交于点、.求证:
(1)是的外接圆的直径;
(2)是的垂直平分线.
?
25.
如图,四边形内接于,,过作垂足为,且.
(1)求证:是的切线;
(2)若,,求的值.
?26.
如图,是的直径,,于点,交于点,交的延长线于点,.
(1)求证:;
(2)求证:是的切线;
(3)若,,求的长.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:直径所在的直线是圆的对称轴,所以①错误;
半径相等的两个半圆是等弧,所以②正确;
能完全重合的两条弧是等弧,所以③错误;
和圆有唯一公共点的直线是圆的切线,所以④错误.
故选.
2.
【答案】
B
3.
【答案】
C
【解答】
解:在图中,,
在图中,,
所以,即两种方案各圆形水池的周边需要的材料一样多.
故选.
4.
【答案】
D
【解答】
解:、∵
,
∴
,
故本选项正确;
、∵
,
∴
,
故本选项正确;
、∵
,,,
∴
,,
∵
,
∴
,
∴
,
故本选项正确;
、不一定等于,
故本选项错误;
故选.
5.
【答案】
C
【解答】
∵
是的直径,是的中点,
∴
,
∵
,
∴
是等腰直角三角形,
∴
,
∵
,
∴
,
∴
,
6.
【答案】
A
【解答】
解:、根据圆周角定理得:的圆周角所对的弦是直径,故本选项正确;
、
如图,符合条件,当和不垂直,故本选项错误;
、
如图,,过半径端点,但是不是圆的切线,故本选项错误;
、如图,
弧和弧长度相等,但是弧和弧不是等弧,故本选项错误;
故选.
7.
【答案】
B
【解答】
解:如图:正方形是最大的正方形,,
延长交于点,
∴
,,,
∵
,半径为,
可设正方形的边长为,
则,,
∴
在直角中,,
解得;
即正方形的边长为.
故选.
8.
【答案】
D
【解答】
解:延长,然后作出过点与格点所在的直线,一定交于格点.如图所示:
正六边形的边长为,则半径是,则,
两平行的边之间距离是:,
则的边上的高是:,
边上的高是:,
则.
故选:.
9.
【答案】
A
【解答】
解:∵
四边形内接于,
∴
,
∴
,
∵
平分,
∴
,
∵
切于,
∴
.故选.
10.
【答案】
D
【解答】
解:∵
,,分别切于,,,交,于,两点,
∴
,,
∴
,,
∴
,
,
∴
,,
即,,
∵
,
∴
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:设扇形的圆心角为,
∵
扇形半径是,弧长为,
∴
,
解得:,
故答案为:.
12.
【答案】
【解答】
解:连接,
∵
是的直径,
∴
,
∵
,
∴
.
故答案为:.
13.
【答案】
【解答】
解:连结,,,,如图,
∵
点为内心,
∴
平分,平分,
∴
,,
∵
,
∴
,
∵
,
∴
,即,
∴
,
∵
为直径,
∴
,
∵
,
∴
,
∴
,
∴
为等腰直角三角形,
∴
,
∴
.
故答案为.
14.
【答案】
【解答】
解:设点是优弧(不与,重合)上的一点,连接、,
∵
.
∴
.
∴
.
故答案是:.
15.
【答案】
【解答】
解:∵
的直径垂直于弦,
∴
弧弧,
∵
,
∴
弧的度数是,
∴
由圆周角定理得:,
故答案为:.
16.
【答案】
【解答】
解:设,,分别是,,,
则,
根据两圆相切,切点一定在连心线上,
则作直线,一定经过点,交圆于另一点,
根据相交弦定理,得,
则
∴
.
17.
【答案】
【解答】
解:过点作于,交于,连接、,如图,
∵
,
∴
,
∴
,,
在中,,
在中,,
当点在和之间时,,
当点不在和之间时,,
∴
、之间的距离为.
故答案为.
18.
【答案】
【解答】
解:∵
四边形中,,
∴
、、在以为圆心,以为半径的圆上;(如图)
∵
,,,
∴
;
故是的倍.
19.
【答案】
或
【解答】
解:作半径于,连接.
由垂径定理得:,
在中,,
当水位上升到圆心以下时??水面宽时,
则,
水面上升的高度为:;
当水位上升到圆心以上时,水面上升的高度为:,
综上可得,水面上升的高度为或.
故答案为:或.
20.
【答案】
【解答】
解:,,
∴
,,.
∴
点运动的第一段弧长.
第二段弧长.
∴
顶点运动到″时,点所经过的路径.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
连接,,
∵
=,
∴
=,
∵
=,
∴
是等边三角形,
∴
==,
∴
的直径=.
【解答】
连接,,
∵
=,
∴
=,
∵
=,
∴
是等边三角形,
∴
==,
∴
的直径=.
22.
【答案】
解:连接,
∵
是直径,
∴
(直径所对的角为),
∴
,
∵
弧所对的圆周角是和,
∴
(在同圆中,同弧所对的圆周角相等),
在中,,,
∴
,
∴
,
∴
.
【解答】
解:连接,
∵
是直径,
∴
(直径所对的角为),
∴
,
∵
弧所对的圆周角是和,
∴
(在同圆中,同弧所对的圆周角相等),
在中,,,
∴
,
∴
,
∴
.
23.
【答案】
解:连接,
∵
和都为所对的圆周角,
∴
,
∵
为的直径,
∴
,
∴
,
∵
,
∴
,
∵
,,
∴
,
∴
.
【解答】
解:连接,
∵
和都为所对的圆周角,
∴
,
∵
为的直径,
∴
,
∴
,
∵
,
∴
,
∵
,,
∴
,
∴
.
24.
【答案】
证明:(1)∵
、分别是的内角与外角的平分线,
∴
,,
∴
,
即,
∴
是的外接圆的直径;
(2)∵
是的平分线,
∴
,
∴
,又是的外接圆的直径,
∴
是的垂直平分线.
【解答】
证明:(1)∵
、分别是的内角与外角的平分线,
∴
,,
∴
,
即,
∴
是的外接圆的直径;
(2)∵
是的平分线,
∴
,
∴
,又是的外接圆的直径,
∴
是的垂直平分线.
25.
【答案】
证明:∵
,
∴
为直径,
∴
,
∵
,
∴
,
∵
,,
∴
,
∵
,
∴
,
∴
,即,
∴
,
∴
是的切线;
过点作,垂足为,如图,则,
∴
,
易证得四边形为矩形,
∴
,
∵
,
∴
,
在中,,
∵
,
∴
,
∴
,即,
∴
.
【解答】
证明:∵
,
∴
为直径,
∴
,
∵
,
∴
,
∵
,,
∴
,
∵
,
∴
,
∴
,即,
∴
,
∴
是的切线;
过点作,垂足为,如图,则,
∴
,
易证得四边形为矩形,
∴
,
∵
,
∴
,
在中,,
∵
,
∴
,
∴
,即,
∴
.
26.
【答案】
(1)证明:∵
,
∴
,
∵
是的直径,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
,
∴
;
(2)证明:如解图,连结,
∵
,
∴
,
由(1)可知,
∵
,
∴
,
∵
,
∴
,
∴
,
∴
,
又∵
为的半径,
∴
是的切线;
(3)解:∵
,
∴
,
在中,
∵
,
,
∴
.
【解答】
(1)证明:∵
,
∴
,
∵
是的直径,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
,
∴
;
(2)证明:如解图,连结,
∵
,
∴
,
由(1)可知,
∵
,
∴
,
∵
,
∴
,
∴
,
∴
,
又∵
为的半径,
∴
是的切线;
(3)解:∵
,∴
,
在中,
∵
,
,
∴
.
