人教版数学九年级下册28.2--解直角三角形及其应用 专题训练(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册28.2--解直角三角形及其应用 专题训练(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 18:55:51 | ||
图片预览




文档简介
人教版数学九年级下册28.2--解直角三角形及其应用
专题训练
一、选择题
在中,,,则cos
B的值是?
???
A.
3
B.
C.
D.
如果一个等腰三角形的底角为,腰长为,那么这个三角形的面积为
A.
B.
C.
D.
小明沿着坡角为的山坡向上走,他走了1000m,则他升高了
A.
B.
500m
C.
D.
1000m
如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是,若,则此斜坡的水平距离AC为
A.
75m
B.
50m
C.
30m
D.
12m
如图,从地面B处测得热气球A的仰角为,从地面C处测得热气球A的仰角为若BC为,则热气球A的高度为?
???
A.
B.
C.
D.
如图,在中,,,AB的垂直平分线MN交AC于D,连接若,则BC的长是?
???
A.
B.
C.
D.
如图,某海监船以的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1h到达B处,测得岛屿P在其北偏西方向,保持航向不变又航行2h到达C处,此时海监船与岛屿P之间的距离即PC的长为?
?
?
A.
40nmile
B.
60nmile
C.
D.
如图是横断面为梯形的河坝,根据图中数据,若,则斜坡BC的坡比等于?
???
A.
B.
C.
D.
在中,,,,欲求的值,最适宜的做法是?
???
A.
计算tan
A的值求出
B.
计算sin
A的值求出
C.
计算cos
A的值求出
D.
先根据sin
B求出,再利用求出
如下图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段斜坡CD到达点D,然后再沿水平方向向右行走40米到达点C,D,E均在同一平面内已知斜坡CD的坡度或坡比,且点C到水平面的距离CF为8米,在E处测得建筑物顶端A的仰角为,则建筑物AB的高度约为???
参考数据:,,
A.
米
B.
224米
C.
274米
D.
米
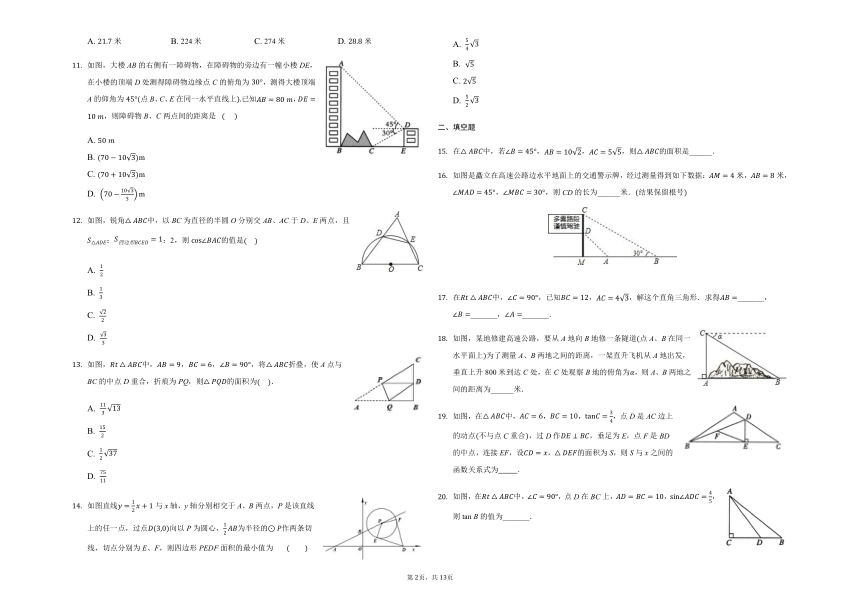
如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为,测得大楼顶端A的仰角为点B、C、E在同一水平直线上已知,,则障碍物B、C两点间的距离是?
???
A.
B.
C.
D.
如图,锐角中,以BC为直径的半圆O分别交AB、AC于D、E两点,且::2,则的值是
A.
B.
C.
D.
如图,中,,,,将折叠,使A点与BC的中点D重合,折痕为PQ,则的面积为.
A.
B.
C.
D.
如图直线与x轴、y轴分别相交于A、B两点,P是该直线上的任一点,过点向以P为圆心,为半径的作两条切线,切点分别为E、F,则四边形PEDF面积的最小值为?
?
???????
A.
B.
C.
D.
二、填空题
在中,若,,,则的面积是______.
如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:米,米,,,则CD的长为______米.结果保留根号
在中,,已知,,解这个直角三角形.求得_______,_______,_______.
如图,某地修建高速公路,要从A地向B地修一条隧道点A、B在同一水平面上为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则A、B两地之间的距离为______米.
如图,在中,,,,点D是AC边上的动点不与点C重合,过D作,垂足为E,点F是BD的中点,连接EF,设,的面积为S,则S与x之间的函数关系式为??????????.
如图,在中,,点D在BC上,,,则tan
B的值为_______.
三、计算题
如图,在中,,,,求BC的长和的值.
如图,在平行四边形ABCD中,E为AD边上一点,BE平分,连接CE,已知,,.
求AB的长;
求平行四边形ABCD的面积;
求.
为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东方向,C在A的南偏西方向处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是,第二组乘公交车,速度是,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由结果保留根号.
如图,AB是的直径,M是OA的中点,弦于点M,过点D作交CA的延长线于点E.
连接AD,求;
点F在上,,DF交AB于点若,求FN的长.
四、解答题(本大题共1小题,共8.0分)
如图,直线与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且,抛物线经过A,B,C三点.
求抛物线的解析式;
点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值.
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查三角函数的定义和等腰三角形的性质.作BC边上的高,利用等腰三角形的性质得BD的长,再利用三角函数定义求解.
【解答】
解:过点A作于D.
在中,,,
,
.
故选B.
2.【答案】B
【解析】
【分析】
本题考查的是等腰三角形的性质,三角形的面积,锐角三角函数的定义有关知识,作底边上的高.运用等腰三角形的性质及三角函数定义分别求三角形的高和底边长,代入公式计算求解.
【解答】
解:如图,作底边上的高AD,
,,AD为高,
则,
,
,
.
故选B.
3.【答案】B
【解析】【试题解析】
解:设他升高了xm,
山坡的坡角为,
,
故选:B.
根据坡角的概念,直角三角形的性质计算即可.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡角的概念是解题的关键.
4.【答案】A
【解析】
【分析】
本题考查解直角三角形的应用坡度坡角问题,解答本题的关键是明确题意,利用数形结合的思想解答.
根据题目中的条件和图形,利用锐角三角函数即可求得AC的长,本题得以解决.
【解答】
解:,,,
,
解得,,
故选A.
5.【答案】B
【解析】
【分析】
本题考查的是解直角三角形的应用仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.过点A作于点D,设米,根据正确的定义用x分别表示出BD、CD,根据题意列出方程,解方程得到答案.
【解答】
解:如图所示,过点A作于点D,
由题意知,,,米,
设米,
,
米,
在中,,
,
由可得,,
解得:.
故选B.
6.【答案】A
【解析】
【分析】
本题考查解直角三角形和线段垂直平分线的性质,解题的关键是由AB的垂直平分线MN交AC于D,,得,在中,,得到,解之即可得到BC的长.
【解答】
解:,,AB的垂直平分线MN交AC于D,
,
.
,
,
解得,
,
.
故选A.
7.【答案】D
【解析】
【分析】
本题考查了解直角三角形的应用方位角问题,首先证明,推出,可得,求出PA即可解决问题.
【解答】
解:在中,
,
,
由题意,
,
,
,
,
,
,
.
故选D.
8.【答案】D
【解析】
【分析】
本题主要考查的是勾股定理,解直角三角形的应用的有关知识,过点D作于F,得到四边形CDFE是矩形,求出EF,DF,然后利用勾股定理求出AF,进而求出BE,最后求解斜坡BC的坡比即可.
【解答】
解:过点D作于F,
则四边形CDFE是矩形,
,,
又,
,
,
斜坡BC的坡比为:,
故选D.
9.【答案】C
【解析】
【分析】
本题主要考查锐角三角函数的定义,解题的关键是掌握正弦、余弦和正切的定义.根据即可得出答案.
【解答】
解:在中,,,,
欲求的值,最适宜的做法是计算的值求出,
故选C.
10.【答案】A
【解析】解:作交ED的延长线于M,
在中,,,
,
四边形BMFC是矩形,
,,,
在中,,
,
米,
故选:A.
作交ED的延长线于M,首先在中,求出DF,再根据,构建方程即可解决问题.
本题考查的是解直角三角形的应用仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
11.【答案】B
【解析】
【分析】
本题考查了解直角三角形仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.
过点D作于点F,过点C作于点通过解直角得到DF的长度;通过解直角得到CE的长度,则.
【解答】
解:如图,过点D作于点F,过点C作于点H.
则,
在直角中,,,
.
在直角中,,,
DE/
,
故选:B.
12.【答案】D
【解析】解:连接CD.
,,
∽.
::2,
::3,
::3,
:3.
故选:D.
要求的余弦值就要构建直角三角形找出相应的边的比例关系,那么可连接CD,通过AD和AC的比例关系来求的余弦值.AD,AC的比例关系可通过∽三来求解,这样就不难求得其余弦值了.
本题主要考查了相似三角形的判定以及圆周角定理,根据三角形相似,用面积比求出相关的线段比是解题的关键.
13.【答案】D
【解析】
【分析】
本题考查了翻折变换,勾股定理,三角形面积公式,锐角三角函数,求出HQ的长是本题的关键.
过点D作于N,过Q作于H,由折叠的性质可得,,由勾股定理可求AQ的长,由锐角三角函数分别求出AP,HQ的长,即可由求解.
【解答】
解:过点D作于N,过Q作于H,
点D是BC中点,
,
将折叠,
,,
,,,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
折叠,
,
故选:D.
14.【答案】A
【解析】
【分析】
本题考查圆的切线的性质,勾股定理,三角形全等,直线与坐标轴的交点.解题的关键是掌握圆的切线的性质.连接DP,根据直线与x轴、y轴分别相交于A、B两点,求得AB的长,即可得出的半径,证≌,可得四边形PEDF面积,当时,四边形PEDF面积的最小,利用锐角三角函数求出DP的长,即可得出四边形PEDF面积的最小值.
【解答】
解:如图,连接DP,
直线与x轴、y轴分别相交于A、B两点,
当时,,当时,,
,,
,
过点向以P为圆心,为半径的作两条切线,切点分别为E、F,
,,
,,
≌,
的半径为,
,
当时,DP最小,此时,
四边形PEDF面积,
四边形PEDF面积的最小值为.
故选A.
15.【答案】75或25
【解析】
【试题解析】
【分析】
本题考查了勾股定理以及三角形的面积,求出AD,BC的长度是解题的关键.
过点A作,垂足为D,通过勾股定理可求出AD,BD,CD的长,进而可得出BC的长,再利用三角形的面积公式可求出的面积.
【解答】
解:过点A作,垂足为D,如图所示.
在中,,;
在中,,,
,
或,
或25.
故答案为:75或25.
16.【答案】
【解析】解:在CMB中,,米,,
,
在中,,,
,
米,
米,
故答案为:.
在中求出CM,在中求出DM即可解决问题.
本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于基础题中考常考题型.
17.【答案】;;
【解析】
【分析】
此题考查了解直角三角形,熟练掌握勾股定理是解本题的关键.在直角三角形ABC中,由BC与AC的值,利用勾股定理求出AB的值即可.
【解答】
解:在中,,,,
根据勾股定理得:,
则,即,
,
故答案为;;.
18.【答案】
【解析】解:在中,,,米,
,
米.
故答案为:.
在中,,,米,根据,即可解决问题.
本题考查解直角三角形的应用仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】x
【解析】
【分析】本题考查解直角三角形,三角形的面积等知识,解题的关键是熟练掌握基本知识.
可在直角三角形CED中,根据DE、CE的长,求出的面积即可解决问题.
【解答】解:在中,,故可设,则,
,,,,
点F是BD的中点,
的面积为的面积的一半,
因此,,
即
20.【答案】
【解析】
【分析】
本题考查的是锐角三角函数,解直角三角形。
根据AD,,求出AC,再根据AC和BC,求出答案。
【解答】
,,
,
在中,,,
.
故答案为。
21.【答案】解:在中,,,,
,
根据勾股定理得:,
则.
【解析】在直角三角形ABC中,根据sinA的值及AB的长,利用锐角三角函数定义求出BC的长,再利用勾股定理求出AC的长,利用锐角三角函数定义即可求出tanB的值.
此题属于解直角三角形,涉及的知识有:锐角三角函数定义,勾股定理,熟练掌握勾股定理是解本题的关键.
22.【答案】解:四边形ABCD是平行四边形,
,
,
平分,
,
,
四边形ABCD是平行四边形.
,
在中,,,,
,
.
,
平行四边形ABCD的面积;
四边形ABCD是平行四边形.
,,
,,
中,,
.
【解析】由平行四边形的性质及角平分线的定义可得出,进而再利用题中数据即可求解结论;
易证为直角三角形,则,基础CE为平行四边形的高,利用平行四边形的面积公式计算即可;
易证,求的值可转化为求的值,利用勾股定理求出BE的长即可.
本题主要考查平行四边形的性质、平行四边形的面积公式运用、解直角三角形的有关知识及角平分线的性质等问题,应熟练掌握.
23.【答案】解:作于D.
依题意得,
,,,
,
.
在中,,,
,
,
,
设,则,
在中,,
,,
,
,
在中,,,
,
,
,
,
,
,,
第一组用时:;第二组用时:,
,
第二组先到达目的地,
答:第一组用时小时,第二组用时小时,第二组先到达目的地.
【解析】过点B作于D,在中证得,设,则,在中,,利用三角函数定义表示出AD的长,在中,利用三角函数表示出CD的长,由列出方程问题得解.
本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.
24.【答案】解:如图1,连接OD,
是的直径,于点
垂直平分CD,
是OA的中点,
,
,
,
,
是等边三角形,
;
如图2,连接CF,CN,
于点M,
点M是CD的中点,
垂直平分CD,
,
,
,
,
,
由可知,,
,
又交CA的延长线于点E,
,
,.
,
,
由可知,,
,
在中,.
【解析】根据垂径定理可得AB垂直平分CD,再根据M是OA的中点及圆的性质,得出是等边三角形即可得出答案;
根据题意得出,计算出CD,CN的长度,根据圆的内接四边形对角互补得出,从而根据三角函数关系计算出FN的值即可.
本题考查了圆的性质、垂径定理、圆的内接四边形的性质、直角三角形的性质、锐角三角函数的应用,正确作出辅助线是解题的关键.
25.【答案】解:由,当时,;当时,,
,,
,
,
,
把,代入抛物线中,得
,解得,
抛物线的解析式为;
点P在二次函数图象上且横坐标为m,
,
过P作轴,交BC于F,则,
,
于点D,
在中,,
,
轴,
,
,
,,
当时,PD最大,最大值为.
【解析】本题考查了二次函数的应用以及解析式的确定、解直角三角形等知识,主要考查学生数形结合思想的应用能力,题目的综合性很强,对学生的解题能力要求很高,是一道不错的中考压轴题.
由直线得出,,即可得出,将A与B坐标代入抛物线解析式求出a与b的值,即可确定出抛物线解析式;
已知P点横坐标,根据直线AB、抛物线的解析式,求出C、P的坐标,由此得到线段PC的长;在中,,根据平行线的性质得出,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
第2页,共2页
第1页,共1页
专题训练
一、选择题
在中,,,则cos
B的值是?
???
A.
3
B.
C.
D.
如果一个等腰三角形的底角为,腰长为,那么这个三角形的面积为
A.
B.
C.
D.
小明沿着坡角为的山坡向上走,他走了1000m,则他升高了
A.
B.
500m
C.
D.
1000m
如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是,若,则此斜坡的水平距离AC为
A.
75m
B.
50m
C.
30m
D.
12m
如图,从地面B处测得热气球A的仰角为,从地面C处测得热气球A的仰角为若BC为,则热气球A的高度为?
???
A.
B.
C.
D.
如图,在中,,,AB的垂直平分线MN交AC于D,连接若,则BC的长是?
???
A.
B.
C.
D.
如图,某海监船以的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1h到达B处,测得岛屿P在其北偏西方向,保持航向不变又航行2h到达C处,此时海监船与岛屿P之间的距离即PC的长为?
?
?
A.
40nmile
B.
60nmile
C.
D.
如图是横断面为梯形的河坝,根据图中数据,若,则斜坡BC的坡比等于?
???
A.
B.
C.
D.
在中,,,,欲求的值,最适宜的做法是?
???
A.
计算tan
A的值求出
B.
计算sin
A的值求出
C.
计算cos
A的值求出
D.
先根据sin
B求出,再利用求出
如下图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段斜坡CD到达点D,然后再沿水平方向向右行走40米到达点C,D,E均在同一平面内已知斜坡CD的坡度或坡比,且点C到水平面的距离CF为8米,在E处测得建筑物顶端A的仰角为,则建筑物AB的高度约为???
参考数据:,,
A.
米
B.
224米
C.
274米
D.
米
如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为,测得大楼顶端A的仰角为点B、C、E在同一水平直线上已知,,则障碍物B、C两点间的距离是?
???
A.
B.
C.
D.
如图,锐角中,以BC为直径的半圆O分别交AB、AC于D、E两点,且::2,则的值是
A.
B.
C.
D.
如图,中,,,,将折叠,使A点与BC的中点D重合,折痕为PQ,则的面积为.
A.
B.
C.
D.
如图直线与x轴、y轴分别相交于A、B两点,P是该直线上的任一点,过点向以P为圆心,为半径的作两条切线,切点分别为E、F,则四边形PEDF面积的最小值为?
?
???????
A.
B.
C.
D.
二、填空题
在中,若,,,则的面积是______.
如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:米,米,,,则CD的长为______米.结果保留根号
在中,,已知,,解这个直角三角形.求得_______,_______,_______.
如图,某地修建高速公路,要从A地向B地修一条隧道点A、B在同一水平面上为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为,则A、B两地之间的距离为______米.
如图,在中,,,,点D是AC边上的动点不与点C重合,过D作,垂足为E,点F是BD的中点,连接EF,设,的面积为S,则S与x之间的函数关系式为??????????.
如图,在中,,点D在BC上,,,则tan
B的值为_______.
三、计算题
如图,在中,,,,求BC的长和的值.
如图,在平行四边形ABCD中,E为AD边上一点,BE平分,连接CE,已知,,.
求AB的长;
求平行四边形ABCD的面积;
求.
为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东方向,C在A的南偏西方向处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是,第二组乘公交车,速度是,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由结果保留根号.
如图,AB是的直径,M是OA的中点,弦于点M,过点D作交CA的延长线于点E.
连接AD,求;
点F在上,,DF交AB于点若,求FN的长.
四、解答题(本大题共1小题,共8.0分)
如图,直线与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且,抛物线经过A,B,C三点.
求抛物线的解析式;
点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值.
答案和解析
1.【答案】B
【解析】
【分析】
本题主要考查三角函数的定义和等腰三角形的性质.作BC边上的高,利用等腰三角形的性质得BD的长,再利用三角函数定义求解.
【解答】
解:过点A作于D.
在中,,,
,
.
故选B.
2.【答案】B
【解析】
【分析】
本题考查的是等腰三角形的性质,三角形的面积,锐角三角函数的定义有关知识,作底边上的高.运用等腰三角形的性质及三角函数定义分别求三角形的高和底边长,代入公式计算求解.
【解答】
解:如图,作底边上的高AD,
,,AD为高,
则,
,
,
.
故选B.
3.【答案】B
【解析】【试题解析】
解:设他升高了xm,
山坡的坡角为,
,
故选:B.
根据坡角的概念,直角三角形的性质计算即可.
本题考查的是解直角三角形的应用坡度坡角问题,掌握坡角的概念是解题的关键.
4.【答案】A
【解析】
【分析】
本题考查解直角三角形的应用坡度坡角问题,解答本题的关键是明确题意,利用数形结合的思想解答.
根据题目中的条件和图形,利用锐角三角函数即可求得AC的长,本题得以解决.
【解答】
解:,,,
,
解得,,
故选A.
5.【答案】B
【解析】
【分析】
本题考查的是解直角三角形的应用仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.过点A作于点D,设米,根据正确的定义用x分别表示出BD、CD,根据题意列出方程,解方程得到答案.
【解答】
解:如图所示,过点A作于点D,
由题意知,,,米,
设米,
,
米,
在中,,
,
由可得,,
解得:.
故选B.
6.【答案】A
【解析】
【分析】
本题考查解直角三角形和线段垂直平分线的性质,解题的关键是由AB的垂直平分线MN交AC于D,,得,在中,,得到,解之即可得到BC的长.
【解答】
解:,,AB的垂直平分线MN交AC于D,
,
.
,
,
解得,
,
.
故选A.
7.【答案】D
【解析】
【分析】
本题考查了解直角三角形的应用方位角问题,首先证明,推出,可得,求出PA即可解决问题.
【解答】
解:在中,
,
,
由题意,
,
,
,
,
,
,
.
故选D.
8.【答案】D
【解析】
【分析】
本题主要考查的是勾股定理,解直角三角形的应用的有关知识,过点D作于F,得到四边形CDFE是矩形,求出EF,DF,然后利用勾股定理求出AF,进而求出BE,最后求解斜坡BC的坡比即可.
【解答】
解:过点D作于F,
则四边形CDFE是矩形,
,,
又,
,
,
斜坡BC的坡比为:,
故选D.
9.【答案】C
【解析】
【分析】
本题主要考查锐角三角函数的定义,解题的关键是掌握正弦、余弦和正切的定义.根据即可得出答案.
【解答】
解:在中,,,,
欲求的值,最适宜的做法是计算的值求出,
故选C.
10.【答案】A
【解析】解:作交ED的延长线于M,
在中,,,
,
四边形BMFC是矩形,
,,,
在中,,
,
米,
故选:A.
作交ED的延长线于M,首先在中,求出DF,再根据,构建方程即可解决问题.
本题考查的是解直角三角形的应用仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
11.【答案】B
【解析】
【分析】
本题考查了解直角三角形仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.
过点D作于点F,过点C作于点通过解直角得到DF的长度;通过解直角得到CE的长度,则.
【解答】
解:如图,过点D作于点F,过点C作于点H.
则,
在直角中,,,
.
在直角中,,,
DE/
,
故选:B.
12.【答案】D
【解析】解:连接CD.
,,
∽.
::2,
::3,
::3,
:3.
故选:D.
要求的余弦值就要构建直角三角形找出相应的边的比例关系,那么可连接CD,通过AD和AC的比例关系来求的余弦值.AD,AC的比例关系可通过∽三来求解,这样就不难求得其余弦值了.
本题主要考查了相似三角形的判定以及圆周角定理,根据三角形相似,用面积比求出相关的线段比是解题的关键.
13.【答案】D
【解析】
【分析】
本题考查了翻折变换,勾股定理,三角形面积公式,锐角三角函数,求出HQ的长是本题的关键.
过点D作于N,过Q作于H,由折叠的性质可得,,由勾股定理可求AQ的长,由锐角三角函数分别求出AP,HQ的长,即可由求解.
【解答】
解:过点D作于N,过Q作于H,
点D是BC中点,
,
将折叠,
,,
,,,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
折叠,
,
故选:D.
14.【答案】A
【解析】
【分析】
本题考查圆的切线的性质,勾股定理,三角形全等,直线与坐标轴的交点.解题的关键是掌握圆的切线的性质.连接DP,根据直线与x轴、y轴分别相交于A、B两点,求得AB的长,即可得出的半径,证≌,可得四边形PEDF面积,当时,四边形PEDF面积的最小,利用锐角三角函数求出DP的长,即可得出四边形PEDF面积的最小值.
【解答】
解:如图,连接DP,
直线与x轴、y轴分别相交于A、B两点,
当时,,当时,,
,,
,
过点向以P为圆心,为半径的作两条切线,切点分别为E、F,
,,
,,
≌,
的半径为,
,
当时,DP最小,此时,
四边形PEDF面积,
四边形PEDF面积的最小值为.
故选A.
15.【答案】75或25
【解析】
【试题解析】
【分析】
本题考查了勾股定理以及三角形的面积,求出AD,BC的长度是解题的关键.
过点A作,垂足为D,通过勾股定理可求出AD,BD,CD的长,进而可得出BC的长,再利用三角形的面积公式可求出的面积.
【解答】
解:过点A作,垂足为D,如图所示.
在中,,;
在中,,,
,
或,
或25.
故答案为:75或25.
16.【答案】
【解析】解:在CMB中,,米,,
,
在中,,,
,
米,
米,
故答案为:.
在中求出CM,在中求出DM即可解决问题.
本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于基础题中考常考题型.
17.【答案】;;
【解析】
【分析】
此题考查了解直角三角形,熟练掌握勾股定理是解本题的关键.在直角三角形ABC中,由BC与AC的值,利用勾股定理求出AB的值即可.
【解答】
解:在中,,,,
根据勾股定理得:,
则,即,
,
故答案为;;.
18.【答案】
【解析】解:在中,,,米,
,
米.
故答案为:.
在中,,,米,根据,即可解决问题.
本题考查解直角三角形的应用仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】x
【解析】
【分析】本题考查解直角三角形,三角形的面积等知识,解题的关键是熟练掌握基本知识.
可在直角三角形CED中,根据DE、CE的长,求出的面积即可解决问题.
【解答】解:在中,,故可设,则,
,,,,
点F是BD的中点,
的面积为的面积的一半,
因此,,
即
20.【答案】
【解析】
【分析】
本题考查的是锐角三角函数,解直角三角形。
根据AD,,求出AC,再根据AC和BC,求出答案。
【解答】
,,
,
在中,,,
.
故答案为。
21.【答案】解:在中,,,,
,
根据勾股定理得:,
则.
【解析】在直角三角形ABC中,根据sinA的值及AB的长,利用锐角三角函数定义求出BC的长,再利用勾股定理求出AC的长,利用锐角三角函数定义即可求出tanB的值.
此题属于解直角三角形,涉及的知识有:锐角三角函数定义,勾股定理,熟练掌握勾股定理是解本题的关键.
22.【答案】解:四边形ABCD是平行四边形,
,
,
平分,
,
,
四边形ABCD是平行四边形.
,
在中,,,,
,
.
,
平行四边形ABCD的面积;
四边形ABCD是平行四边形.
,,
,,
中,,
.
【解析】由平行四边形的性质及角平分线的定义可得出,进而再利用题中数据即可求解结论;
易证为直角三角形,则,基础CE为平行四边形的高,利用平行四边形的面积公式计算即可;
易证,求的值可转化为求的值,利用勾股定理求出BE的长即可.
本题主要考查平行四边形的性质、平行四边形的面积公式运用、解直角三角形的有关知识及角平分线的性质等问题,应熟练掌握.
23.【答案】解:作于D.
依题意得,
,,,
,
.
在中,,,
,
,
,
设,则,
在中,,
,,
,
,
在中,,,
,
,
,
,
,
,,
第一组用时:;第二组用时:,
,
第二组先到达目的地,
答:第一组用时小时,第二组用时小时,第二组先到达目的地.
【解析】过点B作于D,在中证得,设,则,在中,,利用三角函数定义表示出AD的长,在中,利用三角函数表示出CD的长,由列出方程问题得解.
本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.
24.【答案】解:如图1,连接OD,
是的直径,于点
垂直平分CD,
是OA的中点,
,
,
,
,
是等边三角形,
;
如图2,连接CF,CN,
于点M,
点M是CD的中点,
垂直平分CD,
,
,
,
,
,
由可知,,
,
又交CA的延长线于点E,
,
,.
,
,
由可知,,
,
在中,.
【解析】根据垂径定理可得AB垂直平分CD,再根据M是OA的中点及圆的性质,得出是等边三角形即可得出答案;
根据题意得出,计算出CD,CN的长度,根据圆的内接四边形对角互补得出,从而根据三角函数关系计算出FN的值即可.
本题考查了圆的性质、垂径定理、圆的内接四边形的性质、直角三角形的性质、锐角三角函数的应用,正确作出辅助线是解题的关键.
25.【答案】解:由,当时,;当时,,
,,
,
,
,
把,代入抛物线中,得
,解得,
抛物线的解析式为;
点P在二次函数图象上且横坐标为m,
,
过P作轴,交BC于F,则,
,
于点D,
在中,,
,
轴,
,
,
,,
当时,PD最大,最大值为.
【解析】本题考查了二次函数的应用以及解析式的确定、解直角三角形等知识,主要考查学生数形结合思想的应用能力,题目的综合性很强,对学生的解题能力要求很高,是一道不错的中考压轴题.
由直线得出,,即可得出,将A与B坐标代入抛物线解析式求出a与b的值,即可确定出抛物线解析式;
已知P点横坐标,根据直线AB、抛物线的解析式,求出C、P的坐标,由此得到线段PC的长;在中,,根据平行线的性质得出,解直角三角形即可求出PD的表达式,利用二次函数的性质求出PD的最大值即可.
第2页,共2页
第1页,共1页
