高中数学人教A版必修4第二章2.3.1平面向量基本定理题型专题练(Word含解析)
文档属性
| 名称 | 高中数学人教A版必修4第二章2.3.1平面向量基本定理题型专题练(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 08:34:40 | ||
图片预览

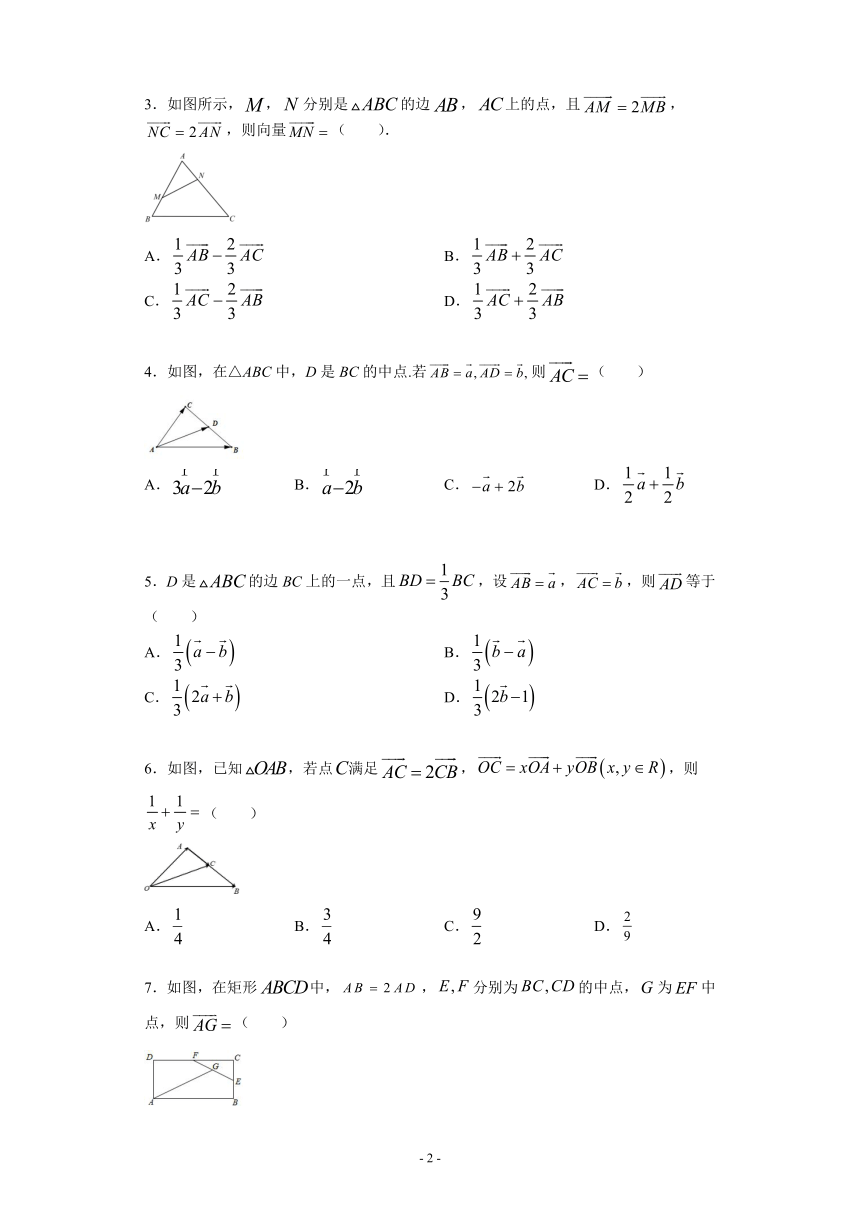



文档简介
《平面向量基本定理》题型专题练
题型一:对基底概念的理解
1.若、是平面内的一组基底,则下四组向量能作为平面向量的基底的是(
).
A.与
B.与
C.与
D.与
2.设、是两不共线的向量,下列四组向量中,不能作为平面向量的一组基底的是(
)
A.和
B.和
C.和
D.和
3.如果是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是(
)
A.与
B.与
C.与
D.与
4.设是平行四边形两对角线的交点,给出下列向量组:①与;②与;③与;④与.其中可作为这个平行四边形所在平面的一组基底的是(
)
A.①②
B.①③
C.①④
D.③④
5.如果与是一组基底,则下列不能作为基底的是(
)
A.与
B.与
C.与
D.与
6.已知是平面向量的一组基底,实数x,y满足,则_________.
题型二:用基底表示向量
1.在△ABC中,已知D为AB上一点,若,则=( )
A.
B.
C.
D.
2.如图,中,E是AB的中点,点F满足,则(
)
A.
B.
C.
D.
3.如图所示,,分别是的边,上的点,且,,则向量(
).
A.
B.
C.
D.
4.如图,在△ABC中,D是BC的中点.若则(
)
A.
B.
C.
D.
5.D是的边BC上的一点,且,设,,则等于(
)
A.
B.
C.
D.
6.如图,已知,若点满足,,则(
)
A.
B.
C.
D.
7.如图,在矩形中,,分别为的中点,为中点,则(
)
A.
B.
C.
D.
8.在中,D为中点,E为上靠近D的三等分点,则(
)
A.
B.
C.
D.
9.如图,在平行四边形中,,E是边上一点,且,则(
)
A.
B.
C.
D.
10.已知平行四边形中,,,,则(
)
A.
B.
C.
D.
11.在中,点在边上且,为的中点,则(
).
A.
B.
C.
D.
12.在△ABC中,,若,则λ+μ=
13.在中,,分别为,边上的点,且,若,则
14.在中,为边的中点,,若,
则
15.如图,在中,点,满足,.若,则
16.在中,已知D是边上一点,若,
则
17.在平行四边形ABCD中,点E,F分别满足,.若,则实数+的值为
18.如图,在中,,是上的一点,若,则实数的值为________.
19.已知的重心为,,,其中,,且,,共线,
则______.
20.如图,在中,.若,则的值为______,P是上的一点,若,则m的值为______.
21.在中,,,与相交于点,设,.
(1)用,表示;
(2)过点作直线分别与线段,交于点,,设,,求证:.
《平面向量基本定理》题型专题练解析
题型一:对基底概念的理解
1.若、是平面内的一组基底,则下四组向量能作为平面向量的基底的是(
).
A.与
B.与
C.与
D.与
【解析】,,故与不能作为基底,故A错误;
,,故与不能作为基底,故B错误;
,,故与不能作为基底,故C错误;
与不共线,故与可以作为基底,故D正确.
2.设、是两不共线的向量,下列四组向量中,不能作为平面向量的一组基底的是(
)
A.和
B.和
C.和
D.和
【解析】,故和共线,不能作为基底.
故选:C.
3.如果是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是(
)
A.与
B.与
C.与
D.与
【解析】对A项,设,则,无解
对B项,设,则,无解
对C项,设,则,无解
对D项,,所以两向量为共线向量,故选:D
4.设是平行四边形两对角线的交点,给出下列向量组:①与;②与;③与;④与.其中可作为这个平行四边形所在平面的一组基底的是(
)
A.①②
B.①③
C.①④
D.③④
【解析】如下图所示:
①与不共线;②,则与共线;③与不共线;④,则与共线.
由平面向量基底的概念知,只有不共线的两个向量才能构成一组基底,故①③满足题意.
故选:B.
5.如果与是一组基底,则下列不能作为基底的是(
)
A.与
B.与
C.与
D.与
【解析】如下图所示,
由于与不共线,则与不共线,A选项中的两个向量不共线,可以作为基底;
如下图所示:
由于与不共线,则与不共线,B选项中的两个向量不共线,可以作为基底;
由题意知,与不共线,,C选项中的两个向量共线,不能作为基底;
与不共线,D选项中的两个向量可以作为基底.故选:C.
6.已知是平面向量的一组基底,实数x,y满足,则_________.
【解析】是平面向量的一组基底,且,
,解得,.
题型二:用基底表示向量
1.在△ABC中,已知D为AB上一点,若,则=( )
A.
B.
C.
D.
【解析】
,故选B.
2.如图,中,E是AB的中点,点F满足,则(
)
A.
B.
C.
D.
【解析】,
故选:A
3.如图所示,,分别是的边,上的点,且,,则向量(
).
A.
B.
C.
D.
【解析】因为,,
所以.故选:C.
4.如图,在△ABC中,D是BC的中点.若则(
)
A.
B.
C.
D.
【解析】可得.
故选:C.
5.D是的边BC上的一点,且,设,,则等于(
)
A.
B.
C.
D.
【解析】由向量的运算法则可得
故选:C.
6.如图,已知,若点满足,,则(
)
A.
B.
C.
D.
【解析】由得,即,
又,所以,因此.
故选:C.
7.如图,在矩形中,,分别为的中点,为中点,则(
)
A.
B.
C.
D.
【解析】根据题意:,
又,
所以,故选:C
8.在中,D为中点,E为上靠近D的三等分点,则(
)
A.
B.
C.
D.
【解析】
,故选:D.
9.如图,在平行四边形中,,E是边上一点,且,则(
)
A.
B.
C.
D.
【解析】由题意,
所以.故选:D.
10.已知平行四边形中,,,,则(
)
A.
B.
C.
D.
【解析】如图所示,
为,,
所以,又,
.
故选:C.
11.在中,点在边上且,为的中点,则(
).
A.
B.
C.
D.
【解析】因为在中,点在边上且,
所以,则,即,
又为的中点,所以,
则.故选:B.
12.在△ABC中,,若,则λ+μ=
【解析】在△ABC中,因为,
所以,
又因为,所以,所以λ+μ=.
13.在中,,分别为,边上的点,且,若,则
【解析】解:如图,
设,且,则:
,
,,解得
14.在中,为边的中点,,若,
则
【解析】因为为边的中点,所以有.
由,因此有.
15.如图,在中,点,满足,.若,则
【解析】因为
,
又,所以,所以.
16.在中,已知D是边上一点,若,
则
【解析】,,
17.在平行四边形ABCD中,点E,F分别满足,.若,则实数+的值为
【解析】由题意,设,则在平行四边形ABCD中,
因为,,所以点E为BC的中点,点F在线段DC上,且,所以,
又因为,且,
所以,
所以,解得,所以。
18.如图,在中,,是上的一点,若,则实数的值为________.
【解析】解法1:因为,所以,
又,所以
因为点三点共线,所以,解得:.
解法2:因为,设,所以,
因为,所以,又,
所以,所以,
又,所以
解得:
,所以.
19.已知的重心为,,,其中,,且,,共线,
则______.
【解析】的重心为,,
,,共线,则存在实数,使得,
,
,解得,.
20.如图,在中,.若,则的值为______,P是上的一点,若,则m的值为______.
【解析】
如图:在中,.所以:,故.
由于点B?P?N三点共线.所以,
则:,整理得:,
故:.所以,解得.
故.
故答案为:①;②.
21.在中,,,与相交于点,设,.
(1)用,表示;
(2)过点作直线分别与线段,交于点,,设,,求证:.
【解析】(1)∵,,三点共线,设,
∴.
同理由,,三点共线可得:,其中,根据平面向量基本定理知:,,,
∴.
(2)由,,三点共线,.
又由(1)知,所以,消去得.
2
2
题型一:对基底概念的理解
1.若、是平面内的一组基底,则下四组向量能作为平面向量的基底的是(
).
A.与
B.与
C.与
D.与
2.设、是两不共线的向量,下列四组向量中,不能作为平面向量的一组基底的是(
)
A.和
B.和
C.和
D.和
3.如果是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是(
)
A.与
B.与
C.与
D.与
4.设是平行四边形两对角线的交点,给出下列向量组:①与;②与;③与;④与.其中可作为这个平行四边形所在平面的一组基底的是(
)
A.①②
B.①③
C.①④
D.③④
5.如果与是一组基底,则下列不能作为基底的是(
)
A.与
B.与
C.与
D.与
6.已知是平面向量的一组基底,实数x,y满足,则_________.
题型二:用基底表示向量
1.在△ABC中,已知D为AB上一点,若,则=( )
A.
B.
C.
D.
2.如图,中,E是AB的中点,点F满足,则(
)
A.
B.
C.
D.
3.如图所示,,分别是的边,上的点,且,,则向量(
).
A.
B.
C.
D.
4.如图,在△ABC中,D是BC的中点.若则(
)
A.
B.
C.
D.
5.D是的边BC上的一点,且,设,,则等于(
)
A.
B.
C.
D.
6.如图,已知,若点满足,,则(
)
A.
B.
C.
D.
7.如图,在矩形中,,分别为的中点,为中点,则(
)
A.
B.
C.
D.
8.在中,D为中点,E为上靠近D的三等分点,则(
)
A.
B.
C.
D.
9.如图,在平行四边形中,,E是边上一点,且,则(
)
A.
B.
C.
D.
10.已知平行四边形中,,,,则(
)
A.
B.
C.
D.
11.在中,点在边上且,为的中点,则(
).
A.
B.
C.
D.
12.在△ABC中,,若,则λ+μ=
13.在中,,分别为,边上的点,且,若,则
14.在中,为边的中点,,若,
则
15.如图,在中,点,满足,.若,则
16.在中,已知D是边上一点,若,
则
17.在平行四边形ABCD中,点E,F分别满足,.若,则实数+的值为
18.如图,在中,,是上的一点,若,则实数的值为________.
19.已知的重心为,,,其中,,且,,共线,
则______.
20.如图,在中,.若,则的值为______,P是上的一点,若,则m的值为______.
21.在中,,,与相交于点,设,.
(1)用,表示;
(2)过点作直线分别与线段,交于点,,设,,求证:.
《平面向量基本定理》题型专题练解析
题型一:对基底概念的理解
1.若、是平面内的一组基底,则下四组向量能作为平面向量的基底的是(
).
A.与
B.与
C.与
D.与
【解析】,,故与不能作为基底,故A错误;
,,故与不能作为基底,故B错误;
,,故与不能作为基底,故C错误;
与不共线,故与可以作为基底,故D正确.
2.设、是两不共线的向量,下列四组向量中,不能作为平面向量的一组基底的是(
)
A.和
B.和
C.和
D.和
【解析】,故和共线,不能作为基底.
故选:C.
3.如果是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是(
)
A.与
B.与
C.与
D.与
【解析】对A项,设,则,无解
对B项,设,则,无解
对C项,设,则,无解
对D项,,所以两向量为共线向量,故选:D
4.设是平行四边形两对角线的交点,给出下列向量组:①与;②与;③与;④与.其中可作为这个平行四边形所在平面的一组基底的是(
)
A.①②
B.①③
C.①④
D.③④
【解析】如下图所示:
①与不共线;②,则与共线;③与不共线;④,则与共线.
由平面向量基底的概念知,只有不共线的两个向量才能构成一组基底,故①③满足题意.
故选:B.
5.如果与是一组基底,则下列不能作为基底的是(
)
A.与
B.与
C.与
D.与
【解析】如下图所示,
由于与不共线,则与不共线,A选项中的两个向量不共线,可以作为基底;
如下图所示:
由于与不共线,则与不共线,B选项中的两个向量不共线,可以作为基底;
由题意知,与不共线,,C选项中的两个向量共线,不能作为基底;
与不共线,D选项中的两个向量可以作为基底.故选:C.
6.已知是平面向量的一组基底,实数x,y满足,则_________.
【解析】是平面向量的一组基底,且,
,解得,.
题型二:用基底表示向量
1.在△ABC中,已知D为AB上一点,若,则=( )
A.
B.
C.
D.
【解析】
,故选B.
2.如图,中,E是AB的中点,点F满足,则(
)
A.
B.
C.
D.
【解析】,
故选:A
3.如图所示,,分别是的边,上的点,且,,则向量(
).
A.
B.
C.
D.
【解析】因为,,
所以.故选:C.
4.如图,在△ABC中,D是BC的中点.若则(
)
A.
B.
C.
D.
【解析】可得.
故选:C.
5.D是的边BC上的一点,且,设,,则等于(
)
A.
B.
C.
D.
【解析】由向量的运算法则可得
故选:C.
6.如图,已知,若点满足,,则(
)
A.
B.
C.
D.
【解析】由得,即,
又,所以,因此.
故选:C.
7.如图,在矩形中,,分别为的中点,为中点,则(
)
A.
B.
C.
D.
【解析】根据题意:,
又,
所以,故选:C
8.在中,D为中点,E为上靠近D的三等分点,则(
)
A.
B.
C.
D.
【解析】
,故选:D.
9.如图,在平行四边形中,,E是边上一点,且,则(
)
A.
B.
C.
D.
【解析】由题意,
所以.故选:D.
10.已知平行四边形中,,,,则(
)
A.
B.
C.
D.
【解析】如图所示,
为,,
所以,又,
.
故选:C.
11.在中,点在边上且,为的中点,则(
).
A.
B.
C.
D.
【解析】因为在中,点在边上且,
所以,则,即,
又为的中点,所以,
则.故选:B.
12.在△ABC中,,若,则λ+μ=
【解析】在△ABC中,因为,
所以,
又因为,所以,所以λ+μ=.
13.在中,,分别为,边上的点,且,若,则
【解析】解:如图,
设,且,则:
,
,,解得
14.在中,为边的中点,,若,
则
【解析】因为为边的中点,所以有.
由,因此有.
15.如图,在中,点,满足,.若,则
【解析】因为
,
又,所以,所以.
16.在中,已知D是边上一点,若,
则
【解析】,,
17.在平行四边形ABCD中,点E,F分别满足,.若,则实数+的值为
【解析】由题意,设,则在平行四边形ABCD中,
因为,,所以点E为BC的中点,点F在线段DC上,且,所以,
又因为,且,
所以,
所以,解得,所以。
18.如图,在中,,是上的一点,若,则实数的值为________.
【解析】解法1:因为,所以,
又,所以
因为点三点共线,所以,解得:.
解法2:因为,设,所以,
因为,所以,又,
所以,所以,
又,所以
解得:
,所以.
19.已知的重心为,,,其中,,且,,共线,
则______.
【解析】的重心为,,
,,共线,则存在实数,使得,
,
,解得,.
20.如图,在中,.若,则的值为______,P是上的一点,若,则m的值为______.
【解析】
如图:在中,.所以:,故.
由于点B?P?N三点共线.所以,
则:,整理得:,
故:.所以,解得.
故.
故答案为:①;②.
21.在中,,,与相交于点,设,.
(1)用,表示;
(2)过点作直线分别与线段,交于点,,设,,求证:.
【解析】(1)∵,,三点共线,设,
∴.
同理由,,三点共线可得:,其中,根据平面向量基本定理知:,,,
∴.
(2)由,,三点共线,.
又由(1)知,所以,消去得.
2
2
