人教版八年级数学下册第17章《勾股定理》17.1第2课时 勾股定理在实际生活中的应用(共19张ppt)
文档属性
| 名称 | 人教版八年级数学下册第17章《勾股定理》17.1第2课时 勾股定理在实际生活中的应用(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 07:54:10 | ||
图片预览






文档简介
(共18张PPT)
17.1
勾股定理
第十七章
勾股定理
第2课时
勾股定理在实际生活中的应用
1.会用勾股定理解决简单的实际问题.
2.树立数形结合的思想.
教学目标
勾股定理的应用
A
B
C
1
m
2
m
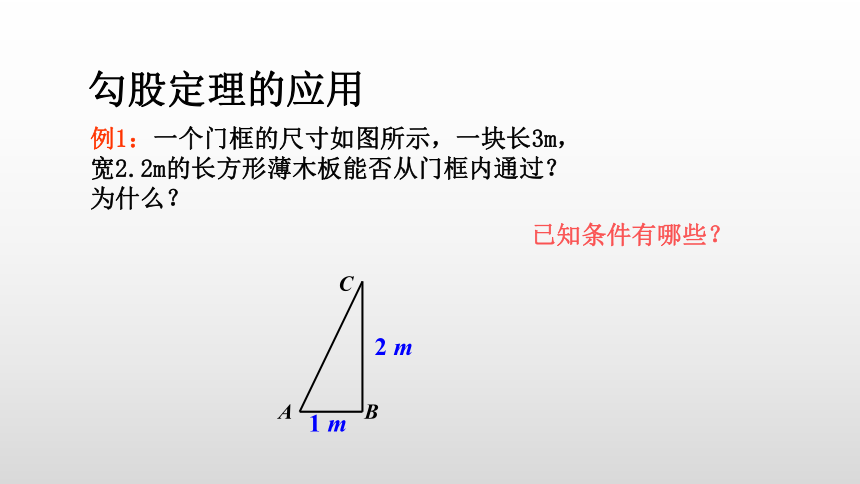
例1:一个门框的尺寸如图所示,一块长3m,
宽2.2m的长方形薄木板能否从门框内通过?
为什么?
已知条件有哪些?
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
3.怎样判定这块木板能否通过木框?
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC=
≈2.24.
因为AC大于木板的宽2.2
m,所
以木板能从门框内通过.
A
B
C
1
m
2
m
例2:一架2.6m长的梯子AB斜靠在一竖直的墙AO上,
这时AO的距离为2.4m.如果梯子顶端A沿墙下滑0.5m,
那么梯子底端B也外移0.5m吗?
独立思考
写出答案
小组交流
展示反馈
解决疑难
解:在Rt△AOB中,根据勾股
定理,
OB2=__________=__________=__
OB=____=______
在Rt△COD中,根据勾股定理,
OD2=_________=____________
=_____
OD=_____≈______
BD=OD-OB≈___________=_______
所以
练习
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60
m,AC=20m.求A,B两点间的距离(结果取整数).
学生独立完成。
一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
2m
1m
A
B
D
C
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
总结
随堂练习
1、如图,△ABC中∠C=90°,AD平分∠BAC,DE⊥AB于E,下面等式错误的是(
)
A、
B、
C、
D、
2.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
?
3.直角三角形中,以直角边为边长的两个正方形面积为7和8,则以斜边为边长的正方形的面积为
15
4.如图,在平面直角坐标系中有两点A(5,0)和B(0,4),求这两点间的距离.
解:
5、如图,山坡的坡角为30°,山坡上两株木之间的坡面距离是
米,则这两株树之间的垂直距离是_____米,水平距离是
米.
6
在数轴上作出表示
的点.
拓展迁移
化非直角三角形为直角三角形
将实际问题转化为直角三角形模型
小技巧
归纳小结
3、学习反思:______________________________________________
_______.
1、勾股定理:
_____________________________________.
______________________________
2、勾股定理有广泛的应用.
如果直角三角形的两直角边长分别为a,b,斜边为c
那么
17.1
勾股定理
第十七章
勾股定理
第2课时
勾股定理在实际生活中的应用
1.会用勾股定理解决简单的实际问题.
2.树立数形结合的思想.
教学目标
勾股定理的应用
A
B
C
1
m
2
m
例1:一个门框的尺寸如图所示,一块长3m,
宽2.2m的长方形薄木板能否从门框内通过?
为什么?
已知条件有哪些?
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
3.怎样判定这块木板能否通过木框?
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC=
≈2.24.
因为AC大于木板的宽2.2
m,所
以木板能从门框内通过.
A
B
C
1
m
2
m
例2:一架2.6m长的梯子AB斜靠在一竖直的墙AO上,
这时AO的距离为2.4m.如果梯子顶端A沿墙下滑0.5m,
那么梯子底端B也外移0.5m吗?
独立思考
写出答案
小组交流
展示反馈
解决疑难
解:在Rt△AOB中,根据勾股
定理,
OB2=__________=__________=__
OB=____=______
在Rt△COD中,根据勾股定理,
OD2=_________=____________
=_____
OD=_____≈______
BD=OD-OB≈___________=_______
所以
练习
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60
m,AC=20m.求A,B两点间的距离(结果取整数).
学生独立完成。
一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能否从门框内通过?为什么?
2m
1m
A
B
D
C
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
总结
随堂练习
1、如图,△ABC中∠C=90°,AD平分∠BAC,DE⊥AB于E,下面等式错误的是(
)
A、
B、
C、
D、
2.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
?
3.直角三角形中,以直角边为边长的两个正方形面积为7和8,则以斜边为边长的正方形的面积为
15
4.如图,在平面直角坐标系中有两点A(5,0)和B(0,4),求这两点间的距离.
解:
5、如图,山坡的坡角为30°,山坡上两株木之间的坡面距离是
米,则这两株树之间的垂直距离是_____米,水平距离是
米.
6
在数轴上作出表示
的点.
拓展迁移
化非直角三角形为直角三角形
将实际问题转化为直角三角形模型
小技巧
归纳小结
3、学习反思:______________________________________________
_______.
1、勾股定理:
_____________________________________.
______________________________
2、勾股定理有广泛的应用.
如果直角三角形的两直角边长分别为a,b,斜边为c
那么
