沪科版(2012)初中数学七年级下册 8.2.3 单项式乘以多项式 教案
文档属性
| 名称 | 沪科版(2012)初中数学七年级下册 8.2.3 单项式乘以多项式 教案 | 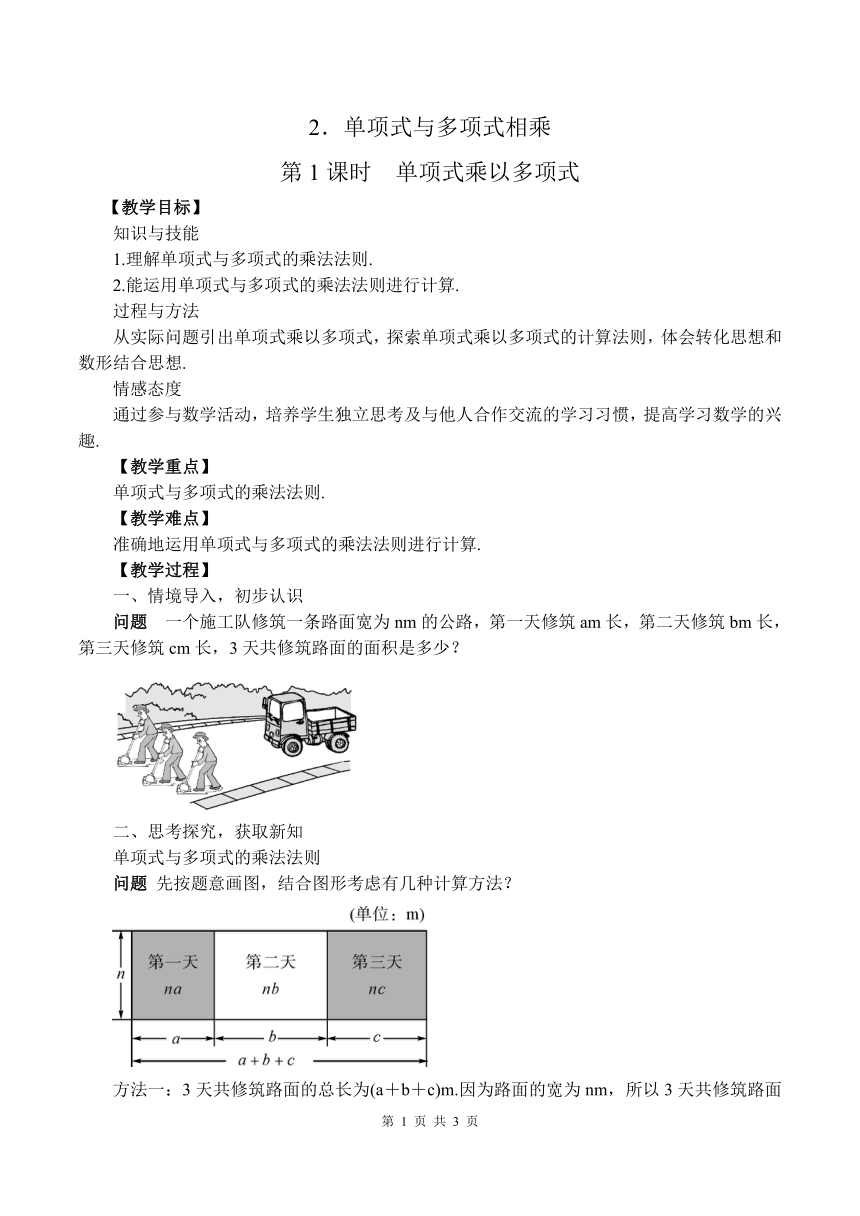 | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 07:49:17 | ||
图片预览

文档简介
2.单项式与多项式相乘
第1课时 单项式乘以多项式
【教学目标】
知识与技能
1.理解单项式与多项式的乘法法则.
2.能运用单项式与多项式的乘法法则进行计算.
过程与方法
从实际问题引出单项式乘以多项式,探索单项式乘以多项式的计算法则,体会转化思想和数形结合思想.
情感态度
通过参与数学活动,培养学生独立思考及与他人合作交流的学习习惯,提高学习数学的兴趣.
【教学重点】
单项式与多项式的乘法法则.
【教学难点】
准确地运用单项式与多项式的乘法法则进行计算.
【教学过程】
一、情境导入,初步认识
问题
一个施工队修筑一条路面宽为nm的公路,第一天修筑am长,第二天修筑bm长,第三天修筑cm长,3天共修筑路面的面积是多少?
二、思考探究,获取新知
单项式与多项式的乘法法则
问题
先按题意画图,结合图形考虑有几种计算方法?
方法一:3天共修筑路面的总长为(a+b+c)m.因为路面的宽为nm,所以3天共修筑路面____m2.
方法二:先分别计算每天修筑路面的面积,然后相加,则3天共修筑路面____m2.因此,有____=____m2.
【归纳结论】
单项式与多项式的乘法法则:单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
三、合作探究
探究点:单项式乘以多项式
【类型一】
直接利用单项式乘以多项式法则进行计算
例1
计算:
(1)(ab2-2ab)·ab;
(2)-2x·(x2y+3y-1).
解析:先去括号,然后计算乘法,再合并同类项即可.
解:(1)(ab2-2ab)·ab=ab2·ab-2ab·ab=a2b3-a2b2;
(2)-2x·(x2y+3y-1)=-2x·x2y+(-2x)·3y-(-2x)·1=-x3y+(-6xy)-(-2x)=-x3y-6xy+2x.
方法总结:单项式与多项式相乘的运算法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
【类型二】
单项式与多项式乘法的实际应用
例2
一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高a米.
(1)求防洪堤坝的横断面积;
(2)如果防洪堤坝长100米,那么这段防洪堤坝的体积是多少立方米?
解析:(1)根据梯形的面积公式,利用单项式乘多项式的法则计算;(2)防洪堤坝的体积=梯形面积×坝长.
解:(1)防洪堤坝的横断面积S=[a+(a+2b)]×a=a(2a+2b)=a2+ab(平方米).故防洪堤坝的横断面积为(a2+ab)平方米;
(2)堤坝的体积V=Sh=(a2+ab)×100=50a2+50ab(立方米).故这段防洪堤坝的体积是(50a2+50ab)立方米.
方法总结:通过本题要知道梯形的面积公式及堤坝的体积(堤坝体积=梯形面积×长度)的计算方法,同时掌握单项式乘多项式的运算法则是解题的关键.
【类型三】
利用单项式乘以多项式化简求值
例3
先化简,再求值:5a(2a2-5a+3)-2a2(5a+5)+7a2,其中a=2.
解析:首先根据单项式与多项式相乘的法则去掉括号,然后合并同类项,最后代入已知的数值计算即可.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2=10a3-25a2+15a-10a3-10a2+7a2=-28a2+15a,当a=2时,原式=-82.
方法总结:本题考查了整式的化简求值.在计算时要注意先化简然后再代值计算.整式的加减运算实际上就是去括号与合并同类项.
四、板书设计
1.单项式与多项式的乘法法则
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
2.单项式与多项式的乘法的应用.
【教学反思】
本节课在已学过的单项式乘单项式的基础上,学习单项式乘多项式.教学中注意发挥学生的主体作用,让学生积极参与课堂活动,并通过不断纠错而提高自主学习能力
第
1
页
共
3
页
第1课时 单项式乘以多项式
【教学目标】
知识与技能
1.理解单项式与多项式的乘法法则.
2.能运用单项式与多项式的乘法法则进行计算.
过程与方法
从实际问题引出单项式乘以多项式,探索单项式乘以多项式的计算法则,体会转化思想和数形结合思想.
情感态度
通过参与数学活动,培养学生独立思考及与他人合作交流的学习习惯,提高学习数学的兴趣.
【教学重点】
单项式与多项式的乘法法则.
【教学难点】
准确地运用单项式与多项式的乘法法则进行计算.
【教学过程】
一、情境导入,初步认识
问题
一个施工队修筑一条路面宽为nm的公路,第一天修筑am长,第二天修筑bm长,第三天修筑cm长,3天共修筑路面的面积是多少?
二、思考探究,获取新知
单项式与多项式的乘法法则
问题
先按题意画图,结合图形考虑有几种计算方法?
方法一:3天共修筑路面的总长为(a+b+c)m.因为路面的宽为nm,所以3天共修筑路面____m2.
方法二:先分别计算每天修筑路面的面积,然后相加,则3天共修筑路面____m2.因此,有____=____m2.
【归纳结论】
单项式与多项式的乘法法则:单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
三、合作探究
探究点:单项式乘以多项式
【类型一】
直接利用单项式乘以多项式法则进行计算
例1
计算:
(1)(ab2-2ab)·ab;
(2)-2x·(x2y+3y-1).
解析:先去括号,然后计算乘法,再合并同类项即可.
解:(1)(ab2-2ab)·ab=ab2·ab-2ab·ab=a2b3-a2b2;
(2)-2x·(x2y+3y-1)=-2x·x2y+(-2x)·3y-(-2x)·1=-x3y+(-6xy)-(-2x)=-x3y-6xy+2x.
方法总结:单项式与多项式相乘的运算法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
【类型二】
单项式与多项式乘法的实际应用
例2
一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高a米.
(1)求防洪堤坝的横断面积;
(2)如果防洪堤坝长100米,那么这段防洪堤坝的体积是多少立方米?
解析:(1)根据梯形的面积公式,利用单项式乘多项式的法则计算;(2)防洪堤坝的体积=梯形面积×坝长.
解:(1)防洪堤坝的横断面积S=[a+(a+2b)]×a=a(2a+2b)=a2+ab(平方米).故防洪堤坝的横断面积为(a2+ab)平方米;
(2)堤坝的体积V=Sh=(a2+ab)×100=50a2+50ab(立方米).故这段防洪堤坝的体积是(50a2+50ab)立方米.
方法总结:通过本题要知道梯形的面积公式及堤坝的体积(堤坝体积=梯形面积×长度)的计算方法,同时掌握单项式乘多项式的运算法则是解题的关键.
【类型三】
利用单项式乘以多项式化简求值
例3
先化简,再求值:5a(2a2-5a+3)-2a2(5a+5)+7a2,其中a=2.
解析:首先根据单项式与多项式相乘的法则去掉括号,然后合并同类项,最后代入已知的数值计算即可.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2=10a3-25a2+15a-10a3-10a2+7a2=-28a2+15a,当a=2时,原式=-82.
方法总结:本题考查了整式的化简求值.在计算时要注意先化简然后再代值计算.整式的加减运算实际上就是去括号与合并同类项.
四、板书设计
1.单项式与多项式的乘法法则
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
2.单项式与多项式的乘法的应用.
【教学反思】
本节课在已学过的单项式乘单项式的基础上,学习单项式乘多项式.教学中注意发挥学生的主体作用,让学生积极参与课堂活动,并通过不断纠错而提高自主学习能力
第
1
页
共
3
页
