沪科版(2012)初中数学八年级下册 18.2 勾股定理及其逆定理复习 教案
文档属性
| 名称 | 沪科版(2012)初中数学八年级下册 18.2 勾股定理及其逆定理复习 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览

文档简介
《勾股定理及其逆定理复习》课教案
课题
勾股定理及其逆定理
课型
复习课
教学目标
1.会用勾股定理解决简单问题;2.会用勾股定理的逆定理判定直角三角形;3.会用勾股定理解决综合问题和实际问题。
教学重点
回顾并思考勾股定理及逆定理。
教学难点
勾股定理及逆定理的应用。
课前准备(教具、活动准备等)
制作课件
教
学
过
程
教学步骤
师生活动
课前预习
1.在直角三角形中,若两直角边的长分别为1cm,2cm
,则斜边长为_____.
斜边上的高为_____.2.已知直角三角形的两边长为3、4,则另一条边长是
_____.3.下列各组数可以构成直角三角形的一组是(????)?
A.3??5??6?????????B.2??3??4?????????????
C.6??7??9?????????D.1.5??2??2.5
知识点回顾知识点回顾
一、勾股定理
1如果直角三角形两直角边分别为a,b,斜边
为c,那么即直角三角形两直角边的平方和等于斜边的平方.2.勾股定理的应用条件:在直角三角形中才可以运用;
3.勾股定理表达式的常见变形:二、勾股定理的逆定理1.勾股定理的逆定理如果三角形的三边长a,b,c满足
,那么这个三角形是直角三角形.勾股数
满足
的三个正整数,称为勾股数.常用的勾股数:3,4,5;
5,12,13;
6,8,10;
7,24,25;
8,15,17
;
9,40,41
勾股定理及其逆定理的应用(一)
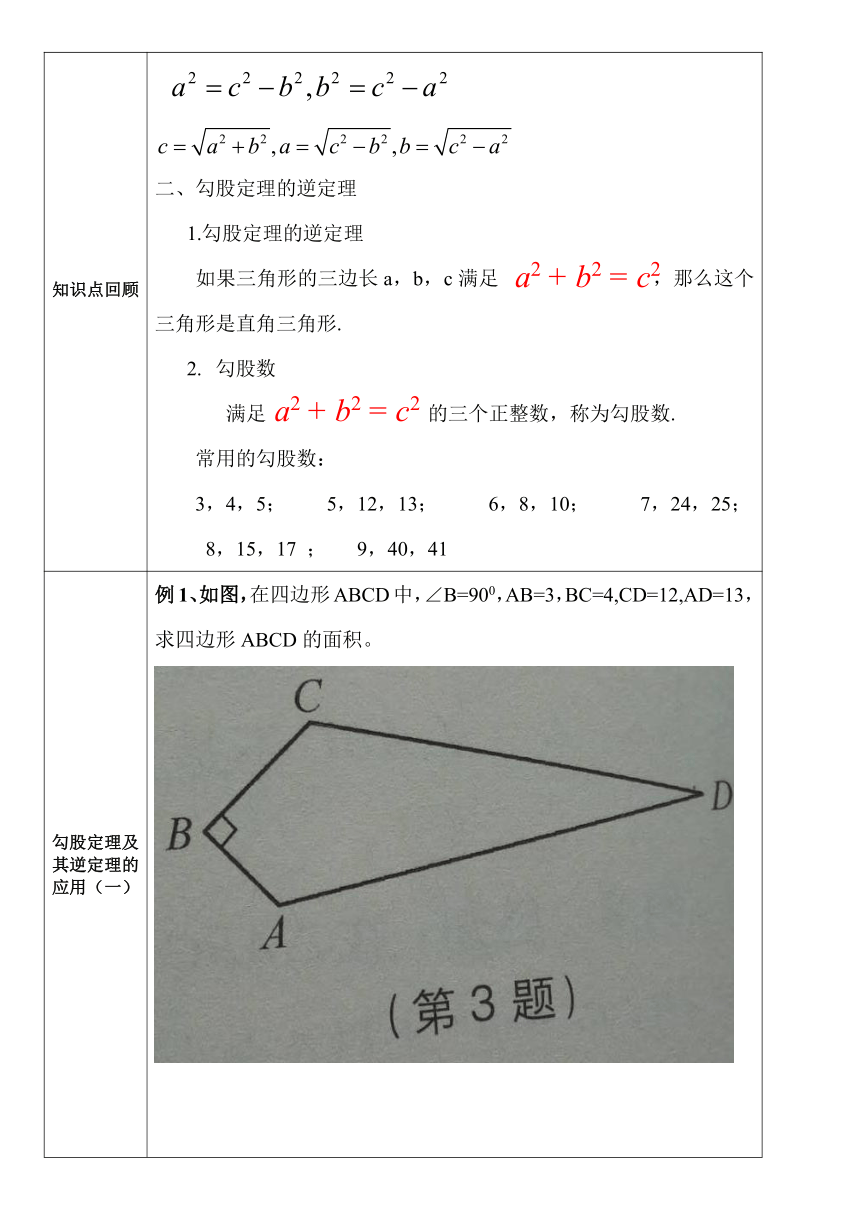
例1、如图,在四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积。例2、边长为8和4的矩形OABC的两边分别在直角坐标系的x轴和y轴上,若沿对角线AC折叠后,点B落在第四象限B1处,设B1C交x轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标。
勾股定理及其逆定理的应用(二)
例3、如图,在直角三角形ABC中,AB=AC,P为BC上任意一点,证明:(1)、(2)。
复习归纳
勾股定理
勾股定理的逆定理
题设
在Rt△ABC
中,∠C=900
在△ABC
中,
三边a,b,c满足a2+b2=c2
结论
a2+b2=c2
∠C=900
作用
1.用勾股定理进行计算2.证明与平方有关的问题3.解决实际问题
1.判断某三角形是否为直角三角形2.解决实际问题
联系
1.两个定理都与“三角形的三边关系a2+b2=c2”有关;2.都与直角三角形有关;3.都是数形结合思想的体现.
课后练习:
在△ABC中,BC=a,AC=b,AB=c设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2与c2的大小关系,可以判断△ABC的形状(按角分类)(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长为6,8,11时,△ABC为_____三角形。(2)小明同学根据上述探究,有下面的猜想:当a2+b2>c2时,△ABC为锐角三角形;当a2+b2a2
+
b2
=
c2
a2
+
b2
=
c2
a2
+
b2
=
c2
O
C
B
A
B1
D
x
y
A
B
P
C
课题
勾股定理及其逆定理
课型
复习课
教学目标
1.会用勾股定理解决简单问题;2.会用勾股定理的逆定理判定直角三角形;3.会用勾股定理解决综合问题和实际问题。
教学重点
回顾并思考勾股定理及逆定理。
教学难点
勾股定理及逆定理的应用。
课前准备(教具、活动准备等)
制作课件
教
学
过
程
教学步骤
师生活动
课前预习
1.在直角三角形中,若两直角边的长分别为1cm,2cm
,则斜边长为_____.
斜边上的高为_____.2.已知直角三角形的两边长为3、4,则另一条边长是
_____.3.下列各组数可以构成直角三角形的一组是(????)?
A.3??5??6?????????B.2??3??4?????????????
C.6??7??9?????????D.1.5??2??2.5
知识点回顾知识点回顾
一、勾股定理
1如果直角三角形两直角边分别为a,b,斜边
为c,那么即直角三角形两直角边的平方和等于斜边的平方.2.勾股定理的应用条件:在直角三角形中才可以运用;
3.勾股定理表达式的常见变形:二、勾股定理的逆定理1.勾股定理的逆定理如果三角形的三边长a,b,c满足
,那么这个三角形是直角三角形.勾股数
满足
的三个正整数,称为勾股数.常用的勾股数:3,4,5;
5,12,13;
6,8,10;
7,24,25;
8,15,17
;
9,40,41
勾股定理及其逆定理的应用(一)
例1、如图,在四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积。例2、边长为8和4的矩形OABC的两边分别在直角坐标系的x轴和y轴上,若沿对角线AC折叠后,点B落在第四象限B1处,设B1C交x轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标。
勾股定理及其逆定理的应用(二)
例3、如图,在直角三角形ABC中,AB=AC,P为BC上任意一点,证明:(1)、(2)。
复习归纳
勾股定理
勾股定理的逆定理
题设
在Rt△ABC
中,∠C=900
在△ABC
中,
三边a,b,c满足a2+b2=c2
结论
a2+b2=c2
∠C=900
作用
1.用勾股定理进行计算2.证明与平方有关的问题3.解决实际问题
1.判断某三角形是否为直角三角形2.解决实际问题
联系
1.两个定理都与“三角形的三边关系a2+b2=c2”有关;2.都与直角三角形有关;3.都是数形结合思想的体现.
课后练习:
在△ABC中,BC=a,AC=b,AB=c设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2与c2的大小关系,可以判断△ABC的形状(按角分类)(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长为6,8,11时,△ABC为_____三角形。(2)小明同学根据上述探究,有下面的猜想:当a2+b2>c2时,△ABC为锐角三角形;当a2+b2
+
b2
=
c2
a2
+
b2
=
c2
a2
+
b2
=
c2
O
C
B
A
B1
D
x
y
A
B
P
C
