人教版八年级上册第十二章全等三角形常考模型分析(无答案)
文档属性
| 名称 | 人教版八年级上册第十二章全等三角形常考模型分析(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 365.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 08:59:05 | ||
图片预览



文档简介
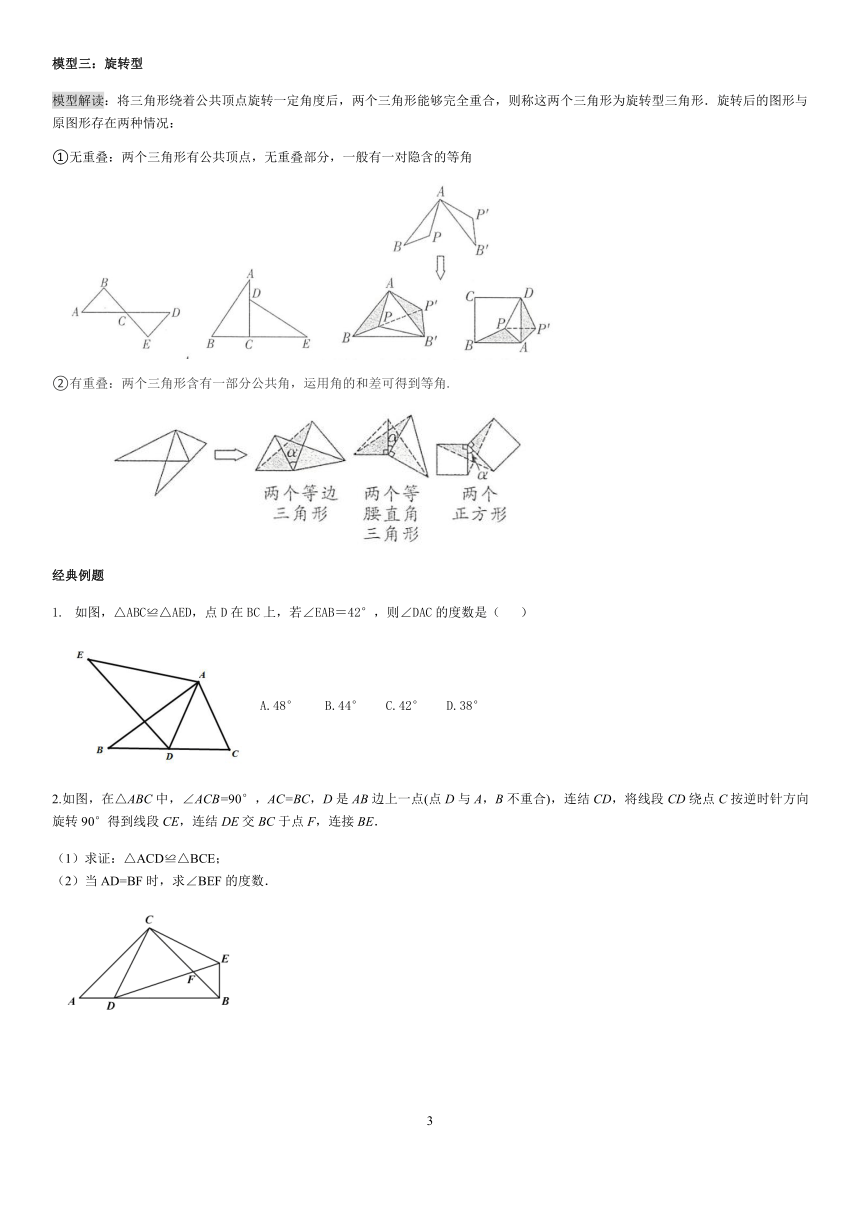
常考全等模型
模型一:平移型
模型分析:此模型特征是有一组边共线或部分重合,另两组边分别平行,常要在移动的方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.
模型示例
经典例题
1.如图,△ABC与△DEF是全等三角形,则图中的相等线段有(
)
A.1
B.2
C.3
D.4
2.如图,点B,E,C,F在同一直线上,AB//DE,AC//DF,BE=CF.求证:AB=DE.
模型二:轴对称模型
模型分析:所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意隐含条件,即公共边或公共角相等.
经典例题
1.如图,,
,
求证:
2.已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
(1)找出图中的全等的三角形,并说明其中一对全等的理由;
(2)说明AO=DO的理由.
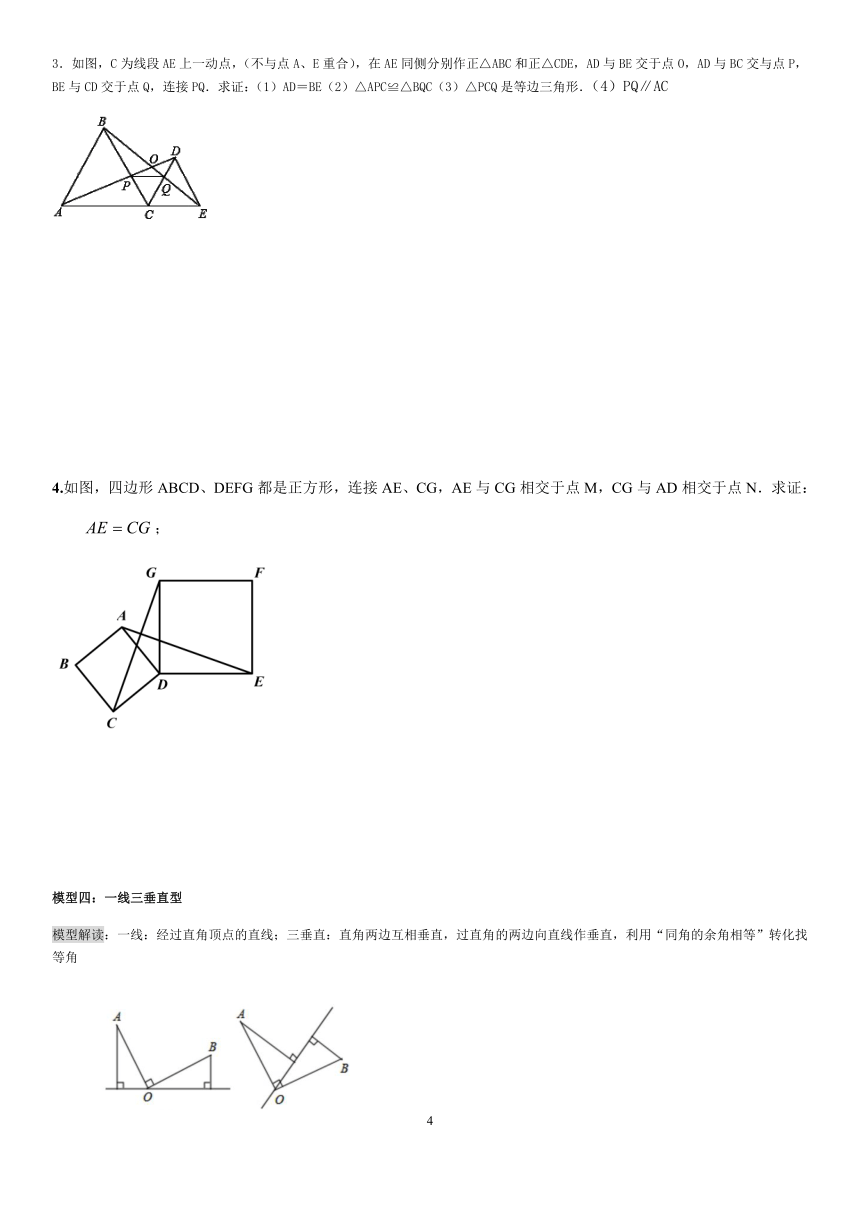
模型三:旋转型
模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形.旋转后的图形与原图形存在两种情况:
①无重叠:两个三角形有公共顶点,无重叠部分,一般有一对隐含的等角
②有重叠:两个三角形含有一部分公共角,运用角的和差可得到等角.
经典例题
如图,△ABC≌△AED,点D在BC上,若∠EAB=42°,则∠DAC的度数是(
)
A.48°
B.44°
C.42°
D.38°
2.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
3.如图,C为线段AE上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交与点P,BE与CD交于点Q,连接PQ.求证:(1)AD=BE(2)△APC≌△BQC(3)△PCQ是等边三角形.(4)PQ∥AC
4.如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.求证:;
模型四:一线三垂直型
模型解读:一线:经过直角顶点的直线;三垂直:直角两边互相垂直,过直角的两边向直线作垂直,利用“同角的余角相等”转化找等角
经典例题
1.如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列结论:①DE=AC,②DE⊥AC,③∠EAF=∠ADF,④∠C=∠ADF,⑤∠C=∠E,其中正确的有
(填序号).
2(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)
如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任
意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
3.如图,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,求证CE,BD,DE的关系。
模型五:其他类型
1.已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;(2)若AD=6,CE=4,求AC的长?
2.如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE;延长AB分别交CD,ED于G,F.
(1)求证:AB=CD;(2)若∠ACB=65°,∠DCE=75°,求∠FGC的度数.
3.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.试探索CF与DE的位置关系,并说明理由.
4.如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;(2)求证:FD∥BC.
5.已知如图,在△ABC中,∠ACB=90°,CE⊥AB于E,D为AB上一点,且AD=AC,AF平分∠CAE交CE于F.求证:FD∥BC.
已知:AB=AE,AB⊥AE,AC=AF,AC⊥AF.求证:EC=FB,EC⊥FB;
7.如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.求证AE、CG的位置关系;
提优训练
1.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE
≌△CAD.
(2)若AD=25cm,BE=8cm,求DE的长.
2.△ABC和△BDE是等边三角形,连接AE、CD,求证:AE=CD.
3.如图,已知AE⊥AB,△ACE≌△AFB,CE与AB、BF分别交于D、M.求证:CE⊥BF.
4.如图,正方形ABCD中,E是CD上一点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,求证:△ABG
≌
△AFG.
5.如图,在线段BD上取一点C,以BC,CD为边分别作正三角形ABC和正三角形ECD,连结AD,交EC于点Q,连结BE,交AC于点P,交AD于点F.
(1)通过旋转,图中可得到哪些全等三角形?(2)求∠BFD的度数;(3)PQ与BD平行吗?若平行,请说明理由.
6.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE
≌△CAD.
(2)若AD=25cm,BE=8cm,求DE的长.
7.如图,AE∥CF,AG,CG分别平分∠EAC和∠FCA,过点G的直线BD⊥AE,交AE于B,交CF于D,求证:AB+CD=AC.
模型一:平移型
模型分析:此模型特征是有一组边共线或部分重合,另两组边分别平行,常要在移动的方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.
模型示例
经典例题
1.如图,△ABC与△DEF是全等三角形,则图中的相等线段有(
)
A.1
B.2
C.3
D.4
2.如图,点B,E,C,F在同一直线上,AB//DE,AC//DF,BE=CF.求证:AB=DE.
模型二:轴对称模型
模型分析:所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意隐含条件,即公共边或公共角相等.
经典例题
1.如图,,
,
求证:
2.已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
(1)找出图中的全等的三角形,并说明其中一对全等的理由;
(2)说明AO=DO的理由.
模型三:旋转型
模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形.旋转后的图形与原图形存在两种情况:
①无重叠:两个三角形有公共顶点,无重叠部分,一般有一对隐含的等角
②有重叠:两个三角形含有一部分公共角,运用角的和差可得到等角.
经典例题
如图,△ABC≌△AED,点D在BC上,若∠EAB=42°,则∠DAC的度数是(
)
A.48°
B.44°
C.42°
D.38°
2.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
3.如图,C为线段AE上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交与点P,BE与CD交于点Q,连接PQ.求证:(1)AD=BE(2)△APC≌△BQC(3)△PCQ是等边三角形.(4)PQ∥AC
4.如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.求证:;
模型四:一线三垂直型
模型解读:一线:经过直角顶点的直线;三垂直:直角两边互相垂直,过直角的两边向直线作垂直,利用“同角的余角相等”转化找等角
经典例题
1.如图所示,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,那么下列结论:①DE=AC,②DE⊥AC,③∠EAF=∠ADF,④∠C=∠ADF,⑤∠C=∠E,其中正确的有
(填序号).
2(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)
如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任
意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
3.如图,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,求证CE,BD,DE的关系。
模型五:其他类型
1.已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;(2)若AD=6,CE=4,求AC的长?
2.如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE;延长AB分别交CD,ED于G,F.
(1)求证:AB=CD;(2)若∠ACB=65°,∠DCE=75°,求∠FGC的度数.
3.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.试探索CF与DE的位置关系,并说明理由.
4.如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;(2)求证:FD∥BC.
5.已知如图,在△ABC中,∠ACB=90°,CE⊥AB于E,D为AB上一点,且AD=AC,AF平分∠CAE交CE于F.求证:FD∥BC.
已知:AB=AE,AB⊥AE,AC=AF,AC⊥AF.求证:EC=FB,EC⊥FB;
7.如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.求证AE、CG的位置关系;
提优训练
1.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE
≌△CAD.
(2)若AD=25cm,BE=8cm,求DE的长.
2.△ABC和△BDE是等边三角形,连接AE、CD,求证:AE=CD.
3.如图,已知AE⊥AB,△ACE≌△AFB,CE与AB、BF分别交于D、M.求证:CE⊥BF.
4.如图,正方形ABCD中,E是CD上一点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,求证:△ABG
≌
△AFG.
5.如图,在线段BD上取一点C,以BC,CD为边分别作正三角形ABC和正三角形ECD,连结AD,交EC于点Q,连结BE,交AC于点P,交AD于点F.
(1)通过旋转,图中可得到哪些全等三角形?(2)求∠BFD的度数;(3)PQ与BD平行吗?若平行,请说明理由.
6.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE
≌△CAD.
(2)若AD=25cm,BE=8cm,求DE的长.
7.如图,AE∥CF,AG,CG分别平分∠EAC和∠FCA,过点G的直线BD⊥AE,交AE于B,交CF于D,求证:AB+CD=AC.
