人教版七年级下册 第五章5.1.1 相交线学案(表格式 无答案)
文档属性
| 名称 | 人教版七年级下册 第五章5.1.1 相交线学案(表格式 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 278.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 08:59:03 | ||
图片预览


文档简介
导学提纲
课题
5.1.1
相交线
主备人
课型
新授课
课时安排
1
总课时数
1
上课日期
学习目标
1.结合具体情境,理解邻补角、对顶角的概念,并能运用它们的性质进行角的计算及解决简单实际问题;
2.通过观察和动手操作,培养实验操作能力,总结解决问题的方法和经验;
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣.
学习重难点
重点:邻补角、对顶角的概念及其性质.
难点:利用邻补角、对顶角的定义和性质求角的大小或找角的关系.
教·学过程
札记
情境导入
1.观察写图片中是否存在线段相交和平行的位置关系?请你画出来
二.探索新知
(一)探究点1:邻补角与对顶角的概念
【找一找】
(1)∠1的邻补角是什么?一个角的邻补角一般有几个?
(2)∠3的对顶角是什么?图中有几组对顶角?分别把它们找出来.
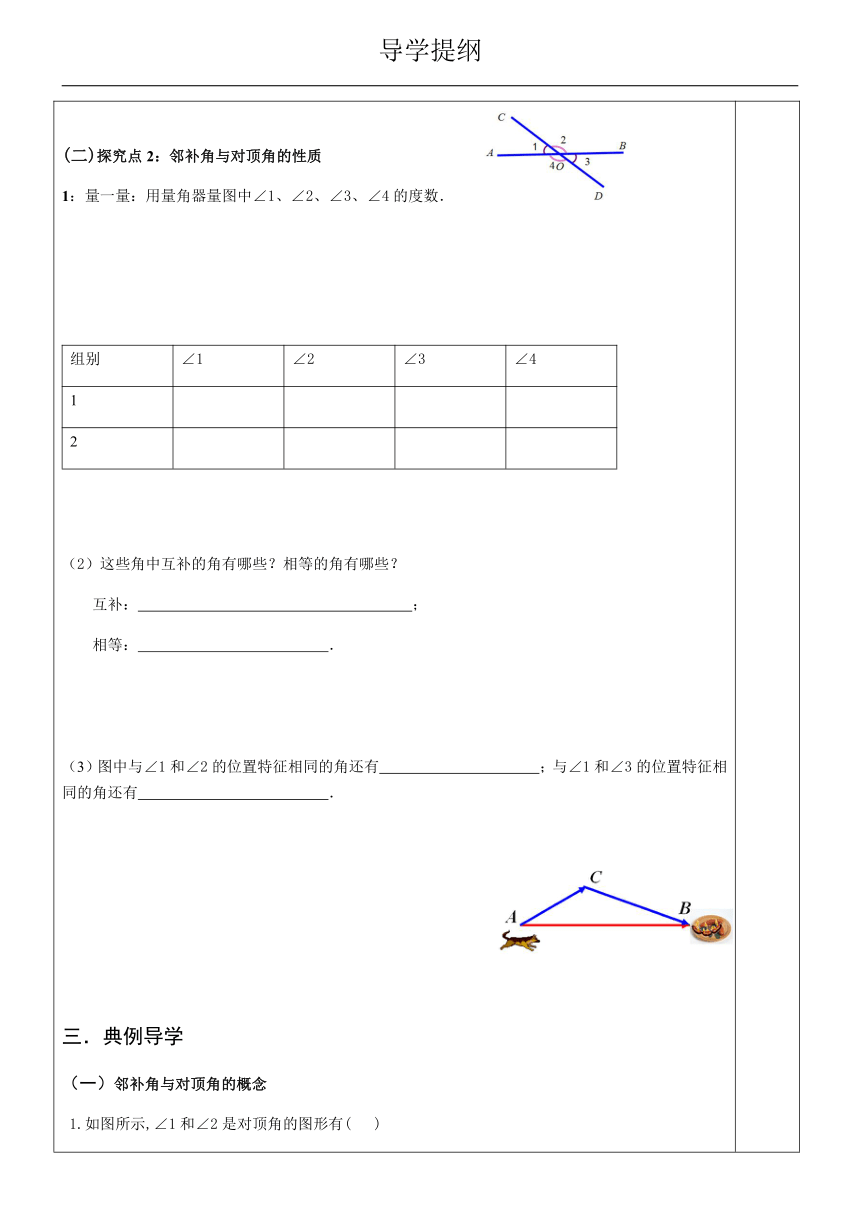
(二)探究点2:邻补角与对顶角的性质
1:量一量:用量角器量图中∠1、∠2、∠3、∠4的度数.
组别∠1∠2∠3∠412
(2)这些角中互补的角有哪些?相等的角有哪些?
互补:
;
相等:
.
(3)图中与∠1和∠2的位置特征相同的角还有
;与∠1和∠3的位置特征相同的角还有
.
三.典例导学
(一)邻补角与对顶角的概念
1.如图所示,∠1和∠2是对顶角的图形有(
)毛
A.1个
B.2个
C.3个
D.4个
A
B
C
D
2.以下说法正确的是(
)
A.一个角的邻补角只有一个
B.相等的两个角是对顶角
C.对顶角一定是相等的两个角
D.互为邻补角的两个角相等
3如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,?且∠BOE:∠EOD=2:3,则∠EOD=________.
(二)邻补角与对顶角的性质
3如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
4如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
四.目标检测
1
1.如图所示,∠1和∠2是对顶角的图形有(
)毛
A.1个
B.2个
C.3个
D.4
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于(
)
A.150°
B.180°
C.210°
D.120°
(1)
(2)
(3)
3.下列说法正确的有(
)
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为(
)
A.62°
B.118°
C.72°
D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是(
)
A.∠1=90°,∠2=30°,∠3=∠4=60°;
B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30°
二、填空题:(每小题3分,共24分)
6.如图4所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
(4)
(5)
7.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
8.如图5所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
四、课堂小结、形成网络
(一)小结
(二)延伸与反思
课题
5.1.1
相交线
主备人
课型
新授课
课时安排
1
总课时数
1
上课日期
学习目标
1.结合具体情境,理解邻补角、对顶角的概念,并能运用它们的性质进行角的计算及解决简单实际问题;
2.通过观察和动手操作,培养实验操作能力,总结解决问题的方法和经验;
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣.
学习重难点
重点:邻补角、对顶角的概念及其性质.
难点:利用邻补角、对顶角的定义和性质求角的大小或找角的关系.
教·学过程
札记
情境导入
1.观察写图片中是否存在线段相交和平行的位置关系?请你画出来
二.探索新知
(一)探究点1:邻补角与对顶角的概念
【找一找】
(1)∠1的邻补角是什么?一个角的邻补角一般有几个?
(2)∠3的对顶角是什么?图中有几组对顶角?分别把它们找出来.
(二)探究点2:邻补角与对顶角的性质
1:量一量:用量角器量图中∠1、∠2、∠3、∠4的度数.
组别∠1∠2∠3∠412
(2)这些角中互补的角有哪些?相等的角有哪些?
互补:
;
相等:
.
(3)图中与∠1和∠2的位置特征相同的角还有
;与∠1和∠3的位置特征相同的角还有
.
三.典例导学
(一)邻补角与对顶角的概念
1.如图所示,∠1和∠2是对顶角的图形有(
)毛
A.1个
B.2个
C.3个
D.4个
A
B
C
D
2.以下说法正确的是(
)
A.一个角的邻补角只有一个
B.相等的两个角是对顶角
C.对顶角一定是相等的两个角
D.互为邻补角的两个角相等
3如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,?且∠BOE:∠EOD=2:3,则∠EOD=________.
(二)邻补角与对顶角的性质
3如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
4如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
四.目标检测
1
1.如图所示,∠1和∠2是对顶角的图形有(
)毛
A.1个
B.2个
C.3个
D.4
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于(
)
A.150°
B.180°
C.210°
D.120°
(1)
(2)
(3)
3.下列说法正确的有(
)
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为(
)
A.62°
B.118°
C.72°
D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是(
)
A.∠1=90°,∠2=30°,∠3=∠4=60°;
B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30°
二、填空题:(每小题3分,共24分)
6.如图4所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
(4)
(5)
7.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
8.如图5所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
四、课堂小结、形成网络
(一)小结
(二)延伸与反思
