第6章一次函数 复习提优测试-苏科版八年级数学上册期末复习(Word版 含答案)
文档属性
| 名称 | 第6章一次函数 复习提优测试-苏科版八年级数学上册期末复习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 868.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 09:38:29 | ||
图片预览



文档简介
一次函数提优测试卷
(时间:60分钟
满分100分)
一、选择题(每小题3分,共24分)
1.某油箱容量为60L的汽车,加满油后行驶了100km,汽油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为,油箱中剩油量为yL,则y与x之间的函数表达式和自变量取值范围分别是(
).
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤x≤500
D.y=60-0.12x,0≤x≤500
2.在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标为(
)
A.(3,-4)
B.(4,-3)
C.(-4,3)
D.(-3,4)
3.已知直线,若,那么该直线不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为km,小刚在青稞地除草比在菜地浇水多用了b
min,则的值分别(
)
A.1、8
B.0.5、12
C.1、12
D.0.5、8
5.将以此函数的图像向上平移2个单位,平移后,若,则的取值范围(
).
A.
B.
C.
D.
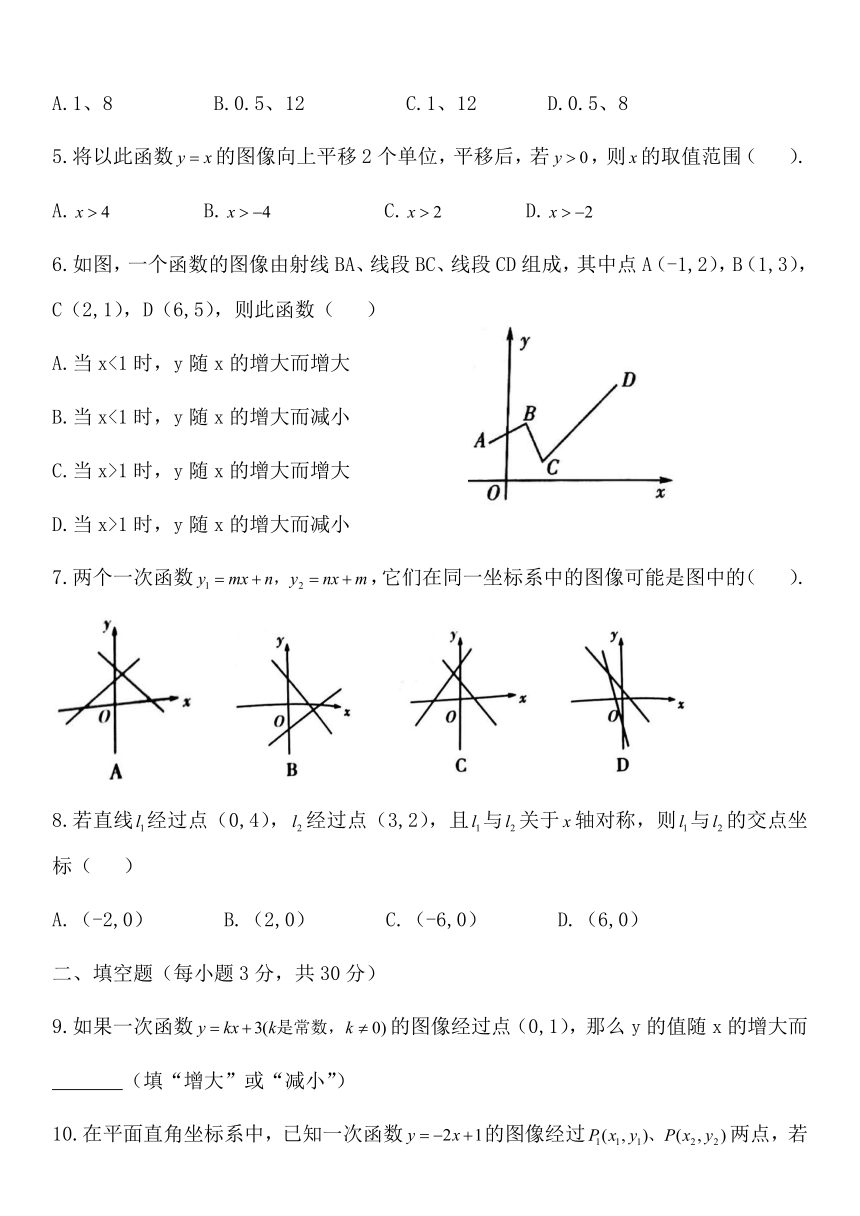
6.如图,一个函数的图像由射线BA、线段BC、线段CD组成,其中点A(-1,2),B(1,3),C(2,1),D(6,5),则此函数(
)
A.当x<1时,y随x的增大而增大
B.当x<1时,y随x的增大而减小
C.当x>1时,y随x的增大而增大
D.当x>1时,y随x的增大而减小
7.两个一次函数,它们在同一坐标系中的图像可能是图中的(
).
8.若直线经过点(0,4),经过点(3,2),且与关于轴对称,则与的交点坐标(
)
A.(-2,0)
B.(2,0)
C.(-6,0)
D.(6,0)
二、填空题(每小题3分,共30分)
9.如果一次函数的图像经过点(0,1),那么y的值随x的增大而
(填“增大”或“减小”)
10.在平面直角坐标系中,已知一次函数的图像经过两点,若,则
.(填“>”“<”“=”)
11.要把直线上、下平移,使其图像经过点(2,10,)需要向
平移
个单位.
12.如图,在平面直角坐标系中,点A、B的坐标分别为(1,3)、(n、3),若直线与线段AB有公共点,则n的值可以为
(写出一个即可).
13.直线与直线相交点(-2,0),且两直线与轴围成的三角形面积为4,那么等于
.
14.如图,直线与的交点的横坐标为-2,则关于的不等式的整数解是
.
15.已知点A(3,0)、B(0,-3)、C(1,m)在同一条直线上,则m=
.
16.如图(1)所示,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图像如图(2)所示,那么△ABC的面积是
.
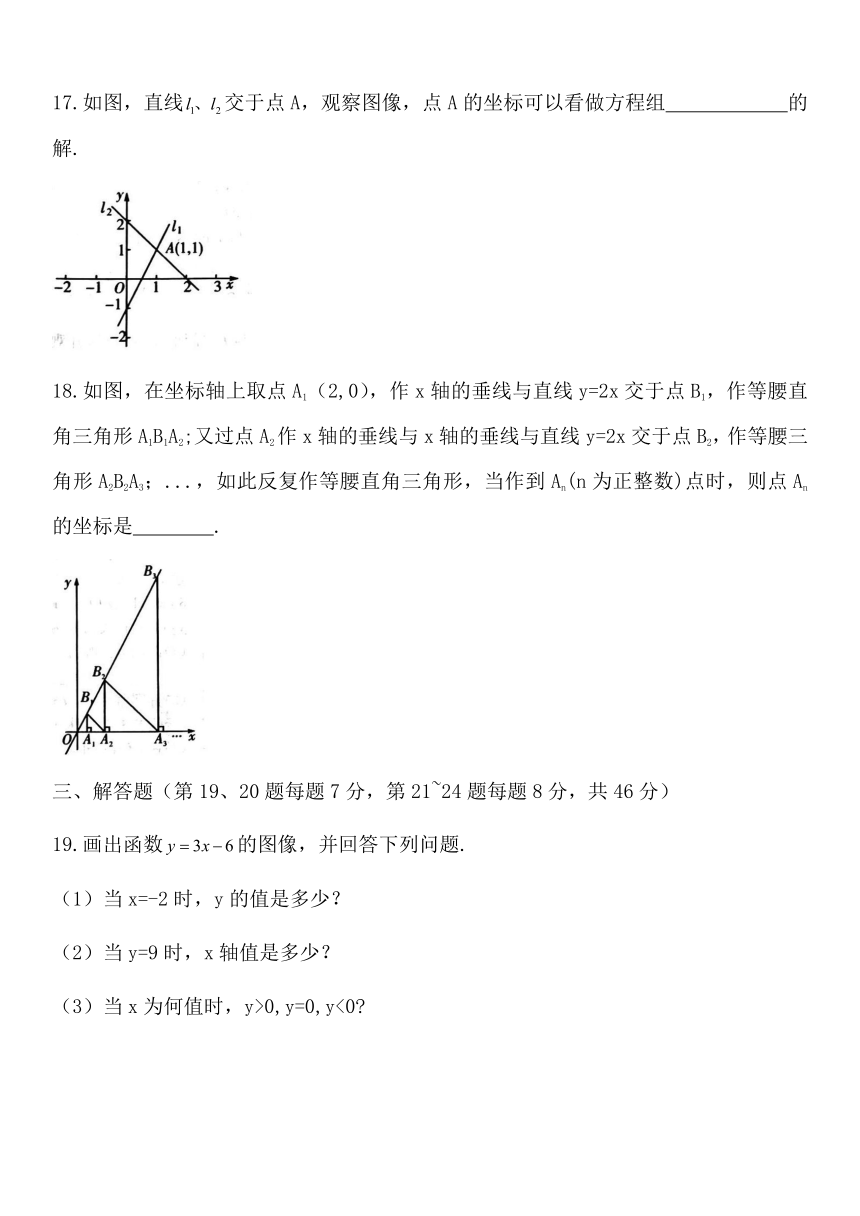
17.如图,直线交于点A,观察图像,点A的坐标可以看做方程组
的解.
18.如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线与x轴的垂线与直线y=2x交于点B2,作等腰三角形A2B2A3;...,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则点An的坐标是
.
三、解答题(第19、20题每题7分,第21~24题每题8分,共46分)
19.画出函数的图像,并回答下列问题.
(1)当x=-2时,y的值是多少?
(2)当y=9时,x轴值是多少?
(3)当x为何值时,y>0,y=0,y<0?
20.我们知道,海拔高度每上升1km,温度下降6℃.某时刻,地面温度为20℃,设高出地面xkm处的温度为y℃.
(1)写出y与x之间的函数表达式;
(2)已知某山峰高出地面约500m,求这时山顶的温度大约是多少?
(3)此刻,有一架飞机飞过上空,若机舱内仪表显示飞机外面的温度为-34℃,求飞机离地面的高度。
21.如图,点A(1,0)、B(4,0)、M(5,3).动点P从点A出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线也随之移动.设移动时间为t秒.
(1)当t=1时,求直线的函数表达式;
(2)若直线与直线BM有公共点,求t的取值范围.
22.赛龙舟是端午节的主要习俗,某市甲、乙两支龙舟队在端午期间进行划龙舟比赛,从起点A驶向终点B,在整个过程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图像解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪只龙舟队先出发?哪只龙舟队先到达终点?
(3)分别求出甲、乙两支龙舟队的y与x的函数表达式;
(4)甲龙舟队出发多长时间,两支龙舟队相距200米?
23.某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图像如图(1)中的点状图所示(5月及以后每月的销售额都相同),二经销成本p(万元)与销售额y(万元)之间函数关系的图像如图(2)中线段AB所示.
(1)求经销成本p(万元)与销售额y(万元)之间的函数表达式.
(2)分别求该公司3月,4月的利润.
(3)把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获的利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额-经销成本)
24.如图(1),长为60km的某线段路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立即返回出发站停止,速度均为30km/h,设甲、乙距南站A的路程分别为行驶时间为t(h).
(1)图(2)已画出与t的函数图像,其中a=
,b=
,c=
;
(2)分别写出0≤t≤2及2<t≤4,与时间t之间的函数表达式;
(3)在图(2)中补画出与t之间的函数图像,并观察图像得出在整个行驶过程中两车相遇的次数.
参考答案
D
C
A
D
D
A
B
B
减小
10.>
11.上
6
12.2
13.4
14.-3
15.-2
16.10
17.
18.
19.图略(1)当x=-2时,y=-12;(2)当y=9时,x=5.(3)当x>2时,y>0;当x=2时,y=0,当x<2时,y<0.
20.(1)y=20-6x
(2)500m=0.5km,当x=0.5时,y=20-6×0.5=17,故温度大约为17℃.
(3)当y=-34时,-34=20-6x,x=9.
故此时飞机离地面高度为9km.
21.(1)直线交x轴于点P(1+t,0)(b>0,t≥0)
当t=1时,1+t=2,
∴P(2,0)
∴-2+b=0,解得b=2.
故当t=1时,直线l的函数表达式为y=-x+2.
(2)当直线y=-x+b过点B(4,0)时,有1+t=4,
∴t=3.
当直线y=-x+b过点M(5,3)时,
有3=-5+b,解得b=8.
∴0=-(1+t)+8,解得t=7.
故若与线段BM有公共点,则t的取值范围是3≤t≤7.
22.(1)由图知,起点A与中点B相距3000米.
(2)由图知:甲龙舟队先出发,乙龙舟队先到达终点.
(3)函数表达式为.
(4)甲龙舟队出发分钟或10分钟或15分钟或分钟时,两龙舟队相距200米.
23.(1)
(2)四月份的利润为77.5万元
(3)最早到第5个月止.
24.(1)60
2
4
(2)当时,设与时间t之间的函数表达式为,由题意得:
解得
所以
当2<t≤4时,设与之间的函数表达式为,由题意,得:
解得:
∴
(3)列表为:
描点并连线为:
如图,由于两个图像有两个交点,所以在整个行驶过程中两车相遇次数为2.
(时间:60分钟
满分100分)
一、选择题(每小题3分,共24分)
1.某油箱容量为60L的汽车,加满油后行驶了100km,汽油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为,油箱中剩油量为yL,则y与x之间的函数表达式和自变量取值范围分别是(
).
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤x≤500
D.y=60-0.12x,0≤x≤500
2.在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标为(
)
A.(3,-4)
B.(4,-3)
C.(-4,3)
D.(-3,4)
3.已知直线,若,那么该直线不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为km,小刚在青稞地除草比在菜地浇水多用了b
min,则的值分别(
)
A.1、8
B.0.5、12
C.1、12
D.0.5、8
5.将以此函数的图像向上平移2个单位,平移后,若,则的取值范围(
).
A.
B.
C.
D.
6.如图,一个函数的图像由射线BA、线段BC、线段CD组成,其中点A(-1,2),B(1,3),C(2,1),D(6,5),则此函数(
)
A.当x<1时,y随x的增大而增大
B.当x<1时,y随x的增大而减小
C.当x>1时,y随x的增大而增大
D.当x>1时,y随x的增大而减小
7.两个一次函数,它们在同一坐标系中的图像可能是图中的(
).
8.若直线经过点(0,4),经过点(3,2),且与关于轴对称,则与的交点坐标(
)
A.(-2,0)
B.(2,0)
C.(-6,0)
D.(6,0)
二、填空题(每小题3分,共30分)
9.如果一次函数的图像经过点(0,1),那么y的值随x的增大而
(填“增大”或“减小”)
10.在平面直角坐标系中,已知一次函数的图像经过两点,若,则
.(填“>”“<”“=”)
11.要把直线上、下平移,使其图像经过点(2,10,)需要向
平移
个单位.
12.如图,在平面直角坐标系中,点A、B的坐标分别为(1,3)、(n、3),若直线与线段AB有公共点,则n的值可以为
(写出一个即可).
13.直线与直线相交点(-2,0),且两直线与轴围成的三角形面积为4,那么等于
.
14.如图,直线与的交点的横坐标为-2,则关于的不等式的整数解是
.
15.已知点A(3,0)、B(0,-3)、C(1,m)在同一条直线上,则m=
.
16.如图(1)所示,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图像如图(2)所示,那么△ABC的面积是
.
17.如图,直线交于点A,观察图像,点A的坐标可以看做方程组
的解.
18.如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线与x轴的垂线与直线y=2x交于点B2,作等腰三角形A2B2A3;...,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则点An的坐标是
.
三、解答题(第19、20题每题7分,第21~24题每题8分,共46分)
19.画出函数的图像,并回答下列问题.
(1)当x=-2时,y的值是多少?
(2)当y=9时,x轴值是多少?
(3)当x为何值时,y>0,y=0,y<0?
20.我们知道,海拔高度每上升1km,温度下降6℃.某时刻,地面温度为20℃,设高出地面xkm处的温度为y℃.
(1)写出y与x之间的函数表达式;
(2)已知某山峰高出地面约500m,求这时山顶的温度大约是多少?
(3)此刻,有一架飞机飞过上空,若机舱内仪表显示飞机外面的温度为-34℃,求飞机离地面的高度。
21.如图,点A(1,0)、B(4,0)、M(5,3).动点P从点A出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线也随之移动.设移动时间为t秒.
(1)当t=1时,求直线的函数表达式;
(2)若直线与直线BM有公共点,求t的取值范围.
22.赛龙舟是端午节的主要习俗,某市甲、乙两支龙舟队在端午期间进行划龙舟比赛,从起点A驶向终点B,在整个过程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图像解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪只龙舟队先出发?哪只龙舟队先到达终点?
(3)分别求出甲、乙两支龙舟队的y与x的函数表达式;
(4)甲龙舟队出发多长时间,两支龙舟队相距200米?
23.某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图像如图(1)中的点状图所示(5月及以后每月的销售额都相同),二经销成本p(万元)与销售额y(万元)之间函数关系的图像如图(2)中线段AB所示.
(1)求经销成本p(万元)与销售额y(万元)之间的函数表达式.
(2)分别求该公司3月,4月的利润.
(3)把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获的利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额-经销成本)
24.如图(1),长为60km的某线段路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立即返回出发站停止,速度均为30km/h,设甲、乙距南站A的路程分别为行驶时间为t(h).
(1)图(2)已画出与t的函数图像,其中a=
,b=
,c=
;
(2)分别写出0≤t≤2及2<t≤4,与时间t之间的函数表达式;
(3)在图(2)中补画出与t之间的函数图像,并观察图像得出在整个行驶过程中两车相遇的次数.
参考答案
D
C
A
D
D
A
B
B
减小
10.>
11.上
6
12.2
13.4
14.-3
15.-2
16.10
17.
18.
19.图略(1)当x=-2时,y=-12;(2)当y=9时,x=5.(3)当x>2时,y>0;当x=2时,y=0,当x<2时,y<0.
20.(1)y=20-6x
(2)500m=0.5km,当x=0.5时,y=20-6×0.5=17,故温度大约为17℃.
(3)当y=-34时,-34=20-6x,x=9.
故此时飞机离地面高度为9km.
21.(1)直线交x轴于点P(1+t,0)(b>0,t≥0)
当t=1时,1+t=2,
∴P(2,0)
∴-2+b=0,解得b=2.
故当t=1时,直线l的函数表达式为y=-x+2.
(2)当直线y=-x+b过点B(4,0)时,有1+t=4,
∴t=3.
当直线y=-x+b过点M(5,3)时,
有3=-5+b,解得b=8.
∴0=-(1+t)+8,解得t=7.
故若与线段BM有公共点,则t的取值范围是3≤t≤7.
22.(1)由图知,起点A与中点B相距3000米.
(2)由图知:甲龙舟队先出发,乙龙舟队先到达终点.
(3)函数表达式为.
(4)甲龙舟队出发分钟或10分钟或15分钟或分钟时,两龙舟队相距200米.
23.(1)
(2)四月份的利润为77.5万元
(3)最早到第5个月止.
24.(1)60
2
4
(2)当时,设与时间t之间的函数表达式为,由题意得:
解得
所以
当2<t≤4时,设与之间的函数表达式为,由题意,得:
解得:
∴
(3)列表为:
描点并连线为:
如图,由于两个图像有两个交点,所以在整个行驶过程中两车相遇次数为2.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
