第6章一次函数 题型专项训练-苏科版八年级数学上册期末复习(word版含答案)
文档属性
| 名称 | 第6章一次函数 题型专项训练-苏科版八年级数学上册期末复习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 08:01:58 | ||
图片预览



文档简介
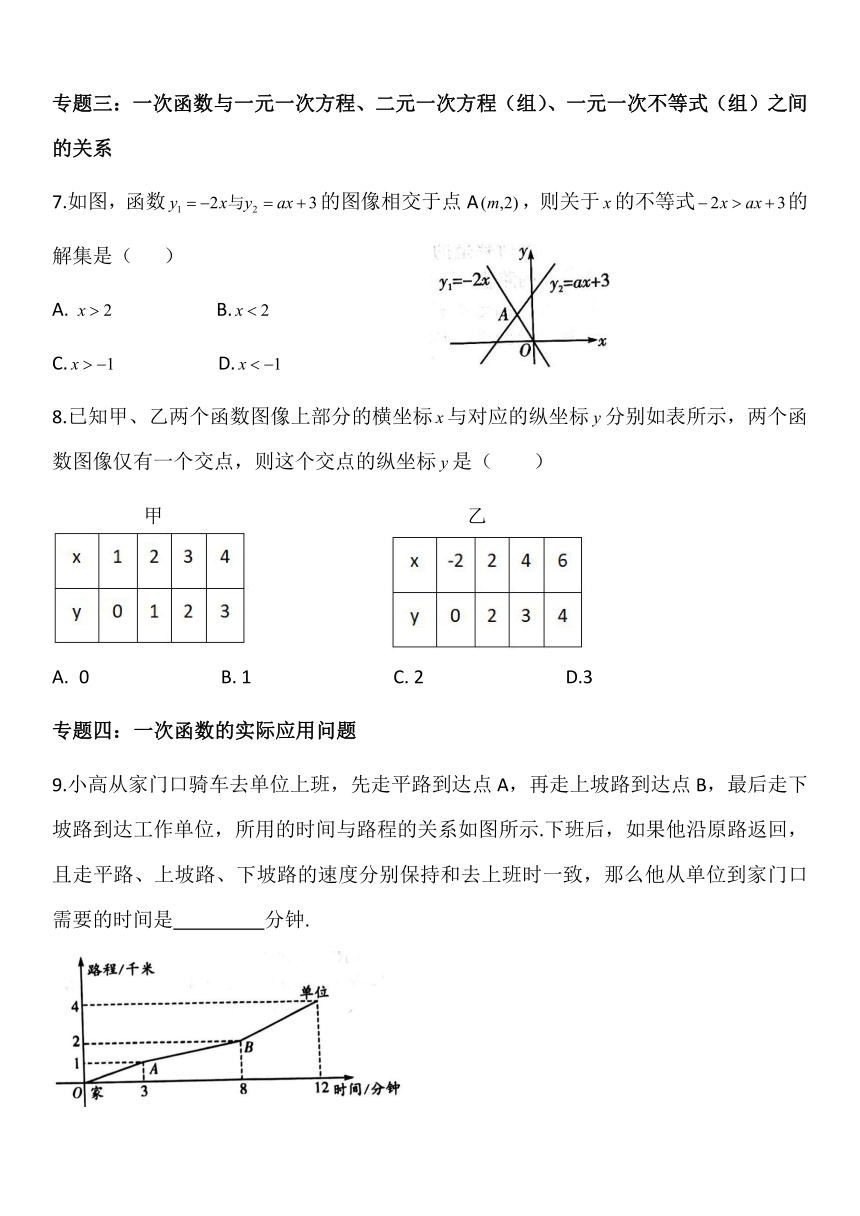
苏科版八年级上册期末复习训练6:一次函数
知识导图:
专题一:函数的概念及图像
1.函数中,自变量的取值范围是(
)
A.
B.
C.
D.
2.为了节能减排,居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.8元/度计算(未超过的部分仍按0.60元/度计算),现假设某用户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图像表示正确的是(
)
专题二:一次函数的相关概念及性质
3.一次函数的图象如图所示,则的取值范围是(
)
A.
B.
C.
D.
4.如图,△AOB是等腰三角形,OA=OB,点B在轴的正半轴上,点A的坐标是(1,1),在点B的坐标是
.
5.若正比例函数(k是常数,且k≠0)的图像经过第二、四象限,则k的值可以是
(写出一个即可).
6.如图,直线与直线相交于点P(1,b).
(1)求b、m的值;
(2)垂直于x轴的直线x=a与直线分别交
于点C,D,若线段CD为2,求a的值.
专题三:一次函数与一元一次方程、二元一次方程(组)、一元一次不等式(组)之间的关系
7.如图,函数的图像相交于点A,则关于的不等式的
解集是(
)
B.
C.
D.
8.已知甲、乙两个函数图像上部分的横坐标与对应的纵坐标分别如表所示,两个函数图像仅有一个交点,则这个交点的纵坐标是(
)
甲
乙
0
B.
1
C.
2
D.3
专题四:一次函数的实际应用问题
9.小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是
分钟.
10.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式.
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
11.某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇用20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
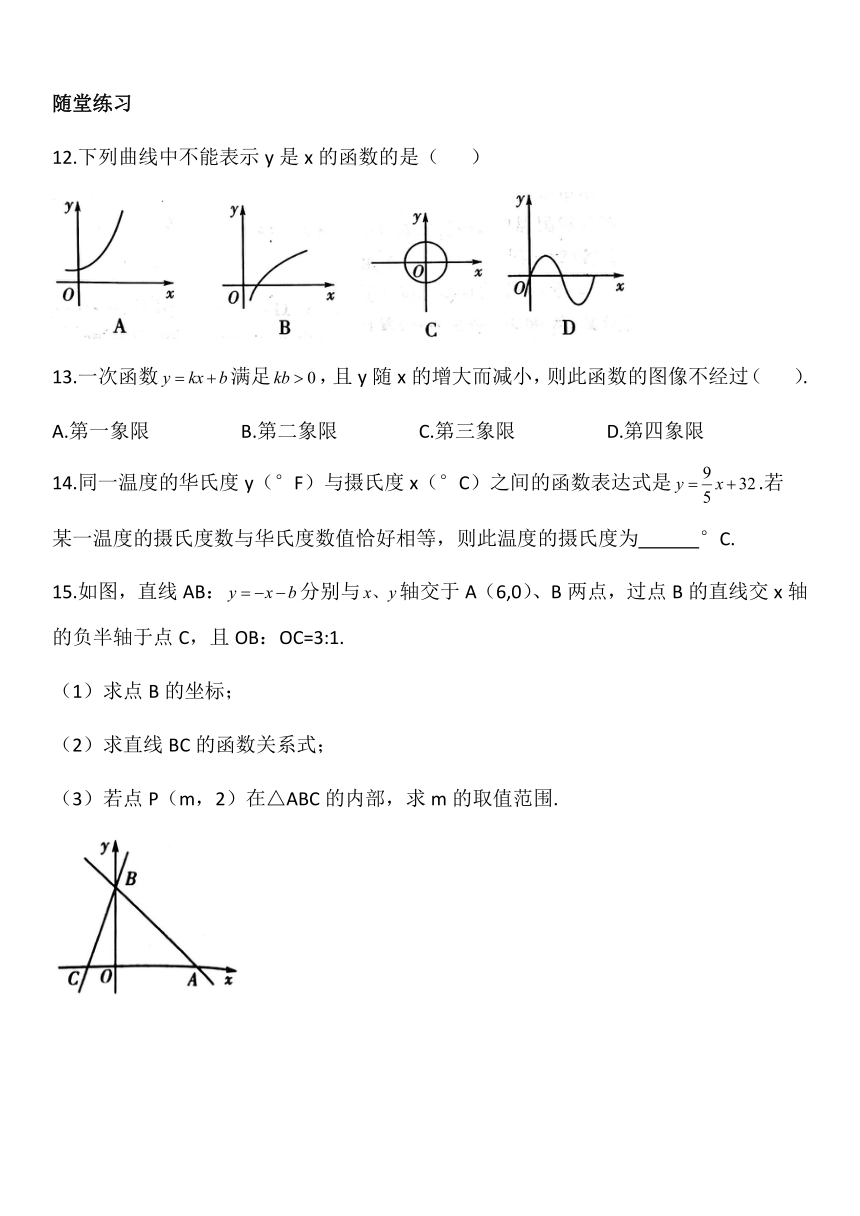
随堂练习
12.下列曲线中不能表示y是x的函数的是(
)
13.一次函数满足,且y随x的增大而减小,则此函数的图像不经过(
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
14.同一温度的华氏度y(°F)与摄氏度x(°C)之间的函数表达式是.若
某一温度的摄氏度数与华氏度数值恰好相等,则此温度的摄氏度为
°C.
15.如图,直线AB:分别与轴交于A(6,0)、B两点,过点B的直线交x轴的负半轴于点C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的函数关系式;
(3)若点P(m,2)在△ABC的内部,求m的取值范围.
16.小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行驶路程y(千米)与校车行驶时间x(分钟)之间的函数图像如图所示.
(1)求点A的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强乘坐的校车?并求此时他们距学校站点的路程.
专项提优特训:融会贯通一次函数
一次函数拥有丰富的题型,例如:分段函数,自变量在不同的取值范围内,其表达式(或图像)也是不同的;最大(小)值,与一元一次不等式(组)相互作用求得多种方案或最值;存在问题,与等腰三角形或直角三角形联合使用确定图形点的坐标;一次函数与图形变换等.
分类训练
类型一:分段函数的应用
1.某公司开发出一款新的节能产品,该产品的成本为6元/件,该产品正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图像,图中的折线ODE表示销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是
件,日销售利润是
元.
(2)求与之间的函数表达式,并写出的其值范围.
(3)日销售利润不低于640元的天数有多少天试销售期间,日销售最大利润是多少元?
2.如图①,某物流公司恰好位于连接A、B两地的一条公路旁的C处,某一天,该公司同时派出甲、乙两辆货车以各自的速度匀速行驶.其中,甲车从公司出发直达B地,乙车从公司出发开往A地,并在A地用1h配货,然后掉头按原始开往B地.图②是甲、乙两地之间的距离s(km)与它们出发后的时间x(h)之间函数关系的部分图象.
(1)由图象可知,甲车速度为
km/h;乙车速度为
km/h;乙车速度为
Km/h.
(2)已知最终乙车比甲车早到B地0.5h,求甲车出发1.5h后直至到达B地的过程中,s与x的函数的取值范围,并在图②中补全函数图象.
3.端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶1小时,再以每小时m千米的速度行驶,途中休息了一段时间后,仍按每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程与时间之间的函数关系式他图像.请根据图像提供的信息,解决下列问题:
(1)图中E点的坐标是
,题中m=
km/h,甲在途中休息
h;
(2)求线段CD的表达式,并写出自变量x的取值范围;
(3)两人第二次相遇后,又经过多长时间两人相距20km?
类型二:一次函数中方案问题
4.某书店现有资金7700元,计划全部用于购进甲、乙、丙三种图书共20套,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元.书店将甲、乙、丙三种图书的售价分别定为每套550元,430元,310元.设书店购进甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数表达式(不需要写出自变量的取值范围).
(2)若书店购进甲、乙两种图书均不少于1套,则该书店有几种进货方案?
(3)在(1)和(2)的条件下,根据市场调查,书店决定将三种图书的售价作出如下调整:甲种图书的售价不变,乙种图书的售价上调a(a为整数)元,丙种图书的售价下调a元,这样三种图书全部售出后,所获得的利润比(2)中某方案的利润多出20元,请直接写出书店是按哪种方案进的货及a的值.
5.某网店销售甲、乙两种防雾霾口罩
,已知甲种口罩每袋的售价比乙种口罩多5元,小丽从该网店网购2袋甲种口罩和3袋乙种口罩共花费110元.
(1)该网店甲、乙两种口罩每袋的售价各是多少元?
(2)根据消费者需求,网店决定用不超过10000元购进甲、乙两种口罩共500袋,且甲种口罩的数量大于乙种口罩的,已知甲种口罩每袋的进价为22.4元,乙种口罩每袋的进价为18元,请你帮助网店计算有几种进货方法.若使网店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元?
类型三:一次函数与图形结合考查
6.如图,在平面直角坐标系中,函数和的图像分别为直线,过点(1,0)作x轴的垂线交于点,过点作y轴的垂线交于点,过点作x轴的垂线交于点作y轴的垂线交于点......依次进行下去,则点的坐标为
.
7.如图,在平面直角坐标系中,已知正比例函数与一次函数的图像交于点A.
(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请求出点M的坐标;
(3)如图,设轴上一点P(a,1),过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图像于点B,C,连接OC,若BC=OA,求△ABC的面积及点B,C的坐标;
(4)在(3)的条件下,设直线交轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请求出点E的坐标.
参考答案
D
C
A
()
-2
6.(1)∵点P(1,b)在直线上,
∴
∵点P(1,3)在直线上,
∴3=m+4
解得m=-1.
(2)当x=a时,;
当时,;
∵CD=2,
∴.
解得或.
7.D
8.D
9.15
10.(1)当时,设函数关系式为,
则,解得.
所以.
(2)4月份上网20小时,应付上网费60元.
(3)由75=3x-30,解得x=35.
所以5月份网35个小时.
11.(1)根据题意,得×40+.
(2)∵
∴
∵为正整数,且,
∴.
∵中,
∴y随x值的增大而减少,
∴当x=7时,y取最大值,
最大值为-350×7+63000=60550.
故安排7名工人采摘,13名工人进行加工,才能使一天的收入最大,最大收入为60550元.
C
A
-40
(1)将点A(6,0)带入直线AB的函数表达式,
得0=-6-b,解得b=-6.
∴直线AB的解析式为
∴点B的坐标为(0,6).
(2)∵OB:OC=3:1,B(0,6),
∴OC=2,
∴点C的坐标为(-2,0)
设BC的函数关系式是,
令0=-2k+6,解得k=3,
∴直线BC的函数关系是,
(3)把代入得
把代入,得.
结合图象可知的取值范围是.
16.(1)∵校车的数为3÷4=0.75(千米/分钟)
∴点A的纵坐标m=3+0.75×(8-6)=4.5.
故点A的纵坐标m的值为4.5.
(2)校车到达学校站点所需时间为9÷0.75+4=16(分钟),
∴出租车的速度为9÷6=1.5(千米/分钟)
∴两车相遇时出租车出发时间为0.75×(9-4)÷(1.5-0.75)=5(分钟).
∴相遇地点离学校站点的路程为9-1.5×5=1.5(千米).
故小刚乘坐出租车出发后经过5分钟追到到小强所乘坐的校车,此时他们距学校站点的路程为1.5千米.
专项提优训练:
1.(1)330
660
(2)y与x之间的函数关系是为
(3)有11天,最大利润为720元.
2.(1)40
80
(2)
补全函数图像如图所所示.
3.(1)(2,160)
100
1
(2)
∴B(4,360),
∴C(5,360),D(7,560)代入,得解得
∴线段CD的表达式为
(3)①当4.5②当x>5时,80x-(100x-140)=20,x=6,6-4.5=1.5(h)
答:两人第二次相遇后,又经过0.25小时或1.5小时两人相距20km.
4.(1)函数表达式为.
(2)根据题意的
又∵x≥1,∴1≤x≤
∵x≥1,∴
∵为整数,∴x=3,6,9
即有三种进货方案:
①甲、乙、丙三种图书分别为3套,13套,4套,
②甲、乙、丙三种图书分别为6套,8套,6套,
③甲、乙、丙三种图书分别为9套,3套,8套.
(3)若按方案一,则有,解得:(舍)
若按方案二,则有,解得:(符合题意)
若按方案三,则有,解得(舍)
所以进货方法是甲、乙、丙三种图书分别为6套,8套,6套,a=10
5.(1)设该网店甲种口罩每袋零售价为x元,乙种口罩每袋的零售价为y元,根据题意得,解得,故该网店甲种口罩每袋的售价为25元,乙种口罩每袋的售价为20元.
(2)设该网店购进甲种口罩m袋,购进乙种口罩(500-m)袋,根据题意得:
解这个不等式组得.
因为m为整数,故有5种进货方案,分别是:购进甲种口罩223袋,乙种口罩277袋;购进甲种口罩224袋,乙种口罩276袋;购进甲种口罩225袋,乙种口罩275袋;
购进甲种口罩226袋,乙种口罩274袋;购进甲种口罩227袋,乙种口罩273袋;
当购进甲种口罩227袋,乙种口罩273袋获利最大,最大利润为1136.2元.
6.()
7.(1)A的坐标为(3,4)
(2)根据勾股定理,得OA=5,
如图①所示,分四种情况考虑,当时,当时,;当时,;当时,.综上所述,点M的坐标为
(3)设点B,∵BC==14,
∴,解得,过点A作AQ⊥BC于点Q,如图②所示,
∴,当a=9时,,,
点B(9,12),C(9,-2).
(4)如图③所示,作D关于直线BC的对称点D′,连接AD′,与直线BC交于点E,连接DE,此时△ADE的周长最小.
对于直线,令,得,即,由(3)得直线BC为直线,
∴D′(11,0).设直线AD′的表达式为,把A与D′的坐标带入,得,解得
所以直线AD′的表达式为.令,得,则此时点E的坐标为(9,1).
知识导图:
专题一:函数的概念及图像
1.函数中,自变量的取值范围是(
)
A.
B.
C.
D.
2.为了节能减排,居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.8元/度计算(未超过的部分仍按0.60元/度计算),现假设某用户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图像表示正确的是(
)
专题二:一次函数的相关概念及性质
3.一次函数的图象如图所示,则的取值范围是(
)
A.
B.
C.
D.
4.如图,△AOB是等腰三角形,OA=OB,点B在轴的正半轴上,点A的坐标是(1,1),在点B的坐标是
.
5.若正比例函数(k是常数,且k≠0)的图像经过第二、四象限,则k的值可以是
(写出一个即可).
6.如图,直线与直线相交于点P(1,b).
(1)求b、m的值;
(2)垂直于x轴的直线x=a与直线分别交
于点C,D,若线段CD为2,求a的值.
专题三:一次函数与一元一次方程、二元一次方程(组)、一元一次不等式(组)之间的关系
7.如图,函数的图像相交于点A,则关于的不等式的
解集是(
)
B.
C.
D.
8.已知甲、乙两个函数图像上部分的横坐标与对应的纵坐标分别如表所示,两个函数图像仅有一个交点,则这个交点的纵坐标是(
)
甲
乙
0
B.
1
C.
2
D.3
专题四:一次函数的实际应用问题
9.小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是
分钟.
10.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式.
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
11.某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇用20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
随堂练习
12.下列曲线中不能表示y是x的函数的是(
)
13.一次函数满足,且y随x的增大而减小,则此函数的图像不经过(
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
14.同一温度的华氏度y(°F)与摄氏度x(°C)之间的函数表达式是.若
某一温度的摄氏度数与华氏度数值恰好相等,则此温度的摄氏度为
°C.
15.如图,直线AB:分别与轴交于A(6,0)、B两点,过点B的直线交x轴的负半轴于点C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的函数关系式;
(3)若点P(m,2)在△ABC的内部,求m的取值范围.
16.小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行驶路程y(千米)与校车行驶时间x(分钟)之间的函数图像如图所示.
(1)求点A的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强乘坐的校车?并求此时他们距学校站点的路程.
专项提优特训:融会贯通一次函数
一次函数拥有丰富的题型,例如:分段函数,自变量在不同的取值范围内,其表达式(或图像)也是不同的;最大(小)值,与一元一次不等式(组)相互作用求得多种方案或最值;存在问题,与等腰三角形或直角三角形联合使用确定图形点的坐标;一次函数与图形变换等.
分类训练
类型一:分段函数的应用
1.某公司开发出一款新的节能产品,该产品的成本为6元/件,该产品正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图像,图中的折线ODE表示销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是
件,日销售利润是
元.
(2)求与之间的函数表达式,并写出的其值范围.
(3)日销售利润不低于640元的天数有多少天试销售期间,日销售最大利润是多少元?
2.如图①,某物流公司恰好位于连接A、B两地的一条公路旁的C处,某一天,该公司同时派出甲、乙两辆货车以各自的速度匀速行驶.其中,甲车从公司出发直达B地,乙车从公司出发开往A地,并在A地用1h配货,然后掉头按原始开往B地.图②是甲、乙两地之间的距离s(km)与它们出发后的时间x(h)之间函数关系的部分图象.
(1)由图象可知,甲车速度为
km/h;乙车速度为
km/h;乙车速度为
Km/h.
(2)已知最终乙车比甲车早到B地0.5h,求甲车出发1.5h后直至到达B地的过程中,s与x的函数的取值范围,并在图②中补全函数图象.
3.端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶1小时,再以每小时m千米的速度行驶,途中休息了一段时间后,仍按每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程与时间之间的函数关系式他图像.请根据图像提供的信息,解决下列问题:
(1)图中E点的坐标是
,题中m=
km/h,甲在途中休息
h;
(2)求线段CD的表达式,并写出自变量x的取值范围;
(3)两人第二次相遇后,又经过多长时间两人相距20km?
类型二:一次函数中方案问题
4.某书店现有资金7700元,计划全部用于购进甲、乙、丙三种图书共20套,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元.书店将甲、乙、丙三种图书的售价分别定为每套550元,430元,310元.设书店购进甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数表达式(不需要写出自变量的取值范围).
(2)若书店购进甲、乙两种图书均不少于1套,则该书店有几种进货方案?
(3)在(1)和(2)的条件下,根据市场调查,书店决定将三种图书的售价作出如下调整:甲种图书的售价不变,乙种图书的售价上调a(a为整数)元,丙种图书的售价下调a元,这样三种图书全部售出后,所获得的利润比(2)中某方案的利润多出20元,请直接写出书店是按哪种方案进的货及a的值.
5.某网店销售甲、乙两种防雾霾口罩
,已知甲种口罩每袋的售价比乙种口罩多5元,小丽从该网店网购2袋甲种口罩和3袋乙种口罩共花费110元.
(1)该网店甲、乙两种口罩每袋的售价各是多少元?
(2)根据消费者需求,网店决定用不超过10000元购进甲、乙两种口罩共500袋,且甲种口罩的数量大于乙种口罩的,已知甲种口罩每袋的进价为22.4元,乙种口罩每袋的进价为18元,请你帮助网店计算有几种进货方法.若使网店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元?
类型三:一次函数与图形结合考查
6.如图,在平面直角坐标系中,函数和的图像分别为直线,过点(1,0)作x轴的垂线交于点,过点作y轴的垂线交于点,过点作x轴的垂线交于点作y轴的垂线交于点......依次进行下去,则点的坐标为
.
7.如图,在平面直角坐标系中,已知正比例函数与一次函数的图像交于点A.
(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请求出点M的坐标;
(3)如图,设轴上一点P(a,1),过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图像于点B,C,连接OC,若BC=OA,求△ABC的面积及点B,C的坐标;
(4)在(3)的条件下,设直线交轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请求出点E的坐标.
参考答案
D
C
A
()
-2
6.(1)∵点P(1,b)在直线上,
∴
∵点P(1,3)在直线上,
∴3=m+4
解得m=-1.
(2)当x=a时,;
当时,;
∵CD=2,
∴.
解得或.
7.D
8.D
9.15
10.(1)当时,设函数关系式为,
则,解得.
所以.
(2)4月份上网20小时,应付上网费60元.
(3)由75=3x-30,解得x=35.
所以5月份网35个小时.
11.(1)根据题意,得×40+.
(2)∵
∴
∵为正整数,且,
∴.
∵中,
∴y随x值的增大而减少,
∴当x=7时,y取最大值,
最大值为-350×7+63000=60550.
故安排7名工人采摘,13名工人进行加工,才能使一天的收入最大,最大收入为60550元.
C
A
-40
(1)将点A(6,0)带入直线AB的函数表达式,
得0=-6-b,解得b=-6.
∴直线AB的解析式为
∴点B的坐标为(0,6).
(2)∵OB:OC=3:1,B(0,6),
∴OC=2,
∴点C的坐标为(-2,0)
设BC的函数关系式是,
令0=-2k+6,解得k=3,
∴直线BC的函数关系是,
(3)把代入得
把代入,得.
结合图象可知的取值范围是.
16.(1)∵校车的数为3÷4=0.75(千米/分钟)
∴点A的纵坐标m=3+0.75×(8-6)=4.5.
故点A的纵坐标m的值为4.5.
(2)校车到达学校站点所需时间为9÷0.75+4=16(分钟),
∴出租车的速度为9÷6=1.5(千米/分钟)
∴两车相遇时出租车出发时间为0.75×(9-4)÷(1.5-0.75)=5(分钟).
∴相遇地点离学校站点的路程为9-1.5×5=1.5(千米).
故小刚乘坐出租车出发后经过5分钟追到到小强所乘坐的校车,此时他们距学校站点的路程为1.5千米.
专项提优训练:
1.(1)330
660
(2)y与x之间的函数关系是为
(3)有11天,最大利润为720元.
2.(1)40
80
(2)
补全函数图像如图所所示.
3.(1)(2,160)
100
1
(2)
∴B(4,360),
∴C(5,360),D(7,560)代入,得解得
∴线段CD的表达式为
(3)①当4.5
答:两人第二次相遇后,又经过0.25小时或1.5小时两人相距20km.
4.(1)函数表达式为.
(2)根据题意的
又∵x≥1,∴1≤x≤
∵x≥1,∴
∵为整数,∴x=3,6,9
即有三种进货方案:
①甲、乙、丙三种图书分别为3套,13套,4套,
②甲、乙、丙三种图书分别为6套,8套,6套,
③甲、乙、丙三种图书分别为9套,3套,8套.
(3)若按方案一,则有,解得:(舍)
若按方案二,则有,解得:(符合题意)
若按方案三,则有,解得(舍)
所以进货方法是甲、乙、丙三种图书分别为6套,8套,6套,a=10
5.(1)设该网店甲种口罩每袋零售价为x元,乙种口罩每袋的零售价为y元,根据题意得,解得,故该网店甲种口罩每袋的售价为25元,乙种口罩每袋的售价为20元.
(2)设该网店购进甲种口罩m袋,购进乙种口罩(500-m)袋,根据题意得:
解这个不等式组得.
因为m为整数,故有5种进货方案,分别是:购进甲种口罩223袋,乙种口罩277袋;购进甲种口罩224袋,乙种口罩276袋;购进甲种口罩225袋,乙种口罩275袋;
购进甲种口罩226袋,乙种口罩274袋;购进甲种口罩227袋,乙种口罩273袋;
当购进甲种口罩227袋,乙种口罩273袋获利最大,最大利润为1136.2元.
6.()
7.(1)A的坐标为(3,4)
(2)根据勾股定理,得OA=5,
如图①所示,分四种情况考虑,当时,当时,;当时,;当时,.综上所述,点M的坐标为
(3)设点B,∵BC==14,
∴,解得,过点A作AQ⊥BC于点Q,如图②所示,
∴,当a=9时,,,
点B(9,12),C(9,-2).
(4)如图③所示,作D关于直线BC的对称点D′,连接AD′,与直线BC交于点E,连接DE,此时△ADE的周长最小.
对于直线,令,得,即,由(3)得直线BC为直线,
∴D′(11,0).设直线AD′的表达式为,把A与D′的坐标带入,得,解得
所以直线AD′的表达式为.令,得,则此时点E的坐标为(9,1).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
