人教版九年级数学上册教学设计:23.2.3 关于原点对称的点的坐标
文档属性
| 名称 | 人教版九年级数学上册教学设计:23.2.3 关于原点对称的点的坐标 |

|
|
| 格式 | zip | ||
| 文件大小 | 66.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 08:16:49 | ||
图片预览


文档简介
九年级数学上册教学设计
课题
23.2.3
关于原点对称的点的坐标
教学
目标
1.理解P点与P′点关于原点对称时,它们的横纵坐标的关系。
2.运用关于原点对称的点的坐标的性质解决画图问题。
教学
重点
成中心对称图形点的坐标的变化规律
教学
难点
用关于原点对称的点的坐标的性质解决画图问题。
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
复习引入
已知点A和点O,如图,请画出点A关于点O的对称的点A′.
A·
O·
新授课
例1.已知:在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:
这些坐标与已知点的坐标有什么关系?
A(-3,1)
B(-4,0)
C(0,3)
D(2,2)
E(3,-3)
F(-2,-2)
总结:两个点关于原点对称时,它们的坐标符号相反,
即点P(x,y)关于原点O的对称点P′
.
例2.如图,利用关于原点对称的点的坐标的特点,
作出与线段AB关于原点对称的图形.
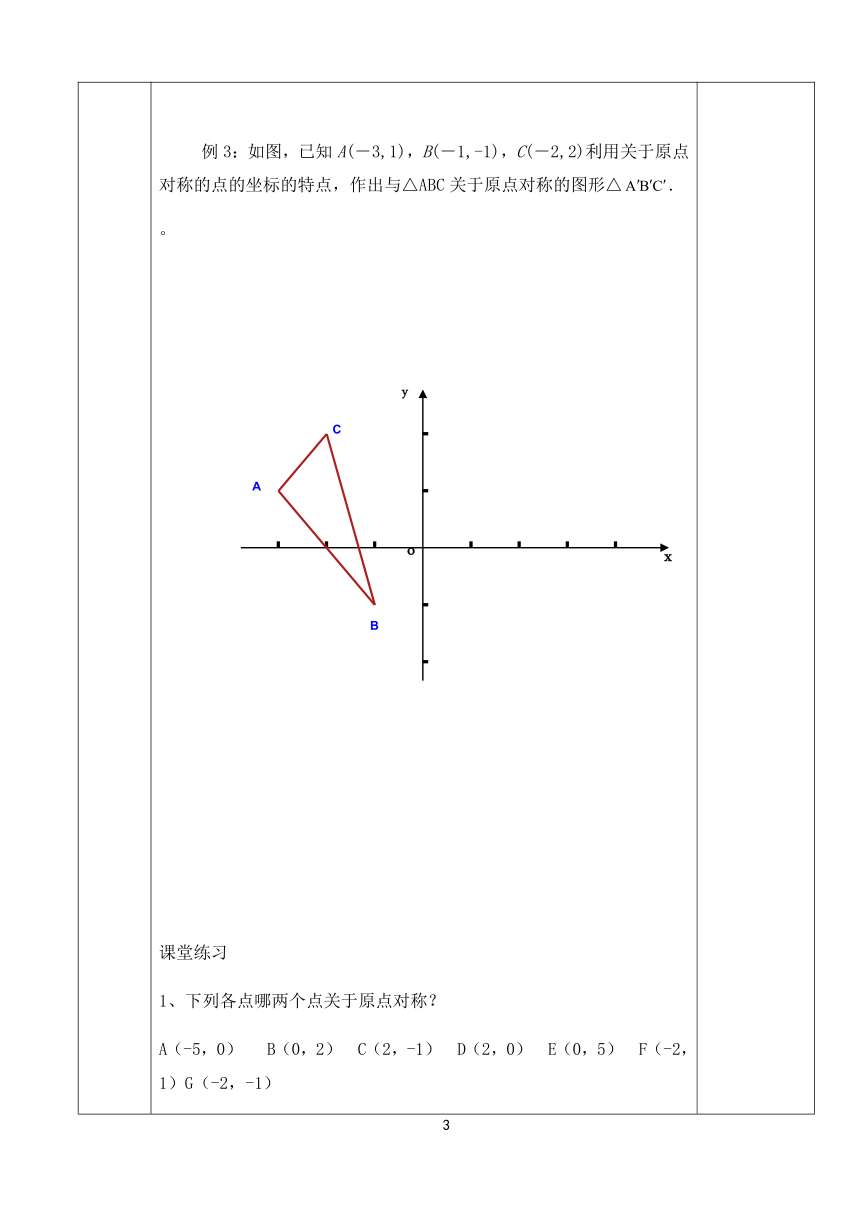
例3:如图,已知A(-3,1),B(-1,-1),C(-2,2)利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形△.
。
课堂练习
1、下列各点哪两个点关于原点对称?
A(-5,0)
B(0,2)
C(2,-1)
D(2,0)
E(0,5)
F(-2,1)G(-2,-1)
2.
点A(-2,1)关于原点对称的点为点B,则点B的坐标为
。
3.
若点A(2,-3)点B(-2,3)则A、B两点关于
对称。
4.
点A(2,-3)关于原点的对称点在第
象限。
5.
已知点P关于x轴的对称点P1的坐标是(2,3),则P关于原点的对称点P2的坐标是
6、已知点A(a,1)与点A1(5,b)是关于原点的对称点,求a,b的值。
7、已知点M()关于原点对称的点在第一象限,那么m的取值范围是
.
8、已知点A(a+1,-3)与点B(-2,b-2)关于y轴对称,则P(-a,b)关于原点的对称点坐标为
9、已知点P关于x轴对称的点P1的坐标是(2,3),则点P关于原点对称的点P2的坐标是
.
10、若点A(a+1,3)与点B(-2,b-2)关于y轴对称,则点P(-a,b)关于原点的对称点坐标为
.
激趣导入,引入主题。
板
书
设
计
点P(x,y)关于原点O的对称点P′
.
点P(x,y)关于x轴的对称点P′
.
点P(x,y)关于y轴的对称点P′
教
学
反
思
1
课题
23.2.3
关于原点对称的点的坐标
教学
目标
1.理解P点与P′点关于原点对称时,它们的横纵坐标的关系。
2.运用关于原点对称的点的坐标的性质解决画图问题。
教学
重点
成中心对称图形点的坐标的变化规律
教学
难点
用关于原点对称的点的坐标的性质解决画图问题。
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
复习引入
已知点A和点O,如图,请画出点A关于点O的对称的点A′.
A·
O·
新授课
例1.已知:在直角坐标系中,已知A(-3,1)、B(-4,0)、C(0,3)、D(2,2)、E(3,-3)、F(-2,-2),作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:
这些坐标与已知点的坐标有什么关系?
A(-3,1)
B(-4,0)
C(0,3)
D(2,2)
E(3,-3)
F(-2,-2)
总结:两个点关于原点对称时,它们的坐标符号相反,
即点P(x,y)关于原点O的对称点P′
.
例2.如图,利用关于原点对称的点的坐标的特点,
作出与线段AB关于原点对称的图形.
例3:如图,已知A(-3,1),B(-1,-1),C(-2,2)利用关于原点对称的点的坐标的特点,作出与△ABC关于原点对称的图形△.
。
课堂练习
1、下列各点哪两个点关于原点对称?
A(-5,0)
B(0,2)
C(2,-1)
D(2,0)
E(0,5)
F(-2,1)G(-2,-1)
2.
点A(-2,1)关于原点对称的点为点B,则点B的坐标为
。
3.
若点A(2,-3)点B(-2,3)则A、B两点关于
对称。
4.
点A(2,-3)关于原点的对称点在第
象限。
5.
已知点P关于x轴的对称点P1的坐标是(2,3),则P关于原点的对称点P2的坐标是
6、已知点A(a,1)与点A1(5,b)是关于原点的对称点,求a,b的值。
7、已知点M()关于原点对称的点在第一象限,那么m的取值范围是
.
8、已知点A(a+1,-3)与点B(-2,b-2)关于y轴对称,则P(-a,b)关于原点的对称点坐标为
9、已知点P关于x轴对称的点P1的坐标是(2,3),则点P关于原点对称的点P2的坐标是
.
10、若点A(a+1,3)与点B(-2,b-2)关于y轴对称,则点P(-a,b)关于原点的对称点坐标为
.
激趣导入,引入主题。
板
书
设
计
点P(x,y)关于原点O的对称点P′
.
点P(x,y)关于x轴的对称点P′
.
点P(x,y)关于y轴的对称点P′
教
学
反
思
1
同课章节目录
