2019-2020学年山东省威海市七年级上册期末数学试卷(五四学制)(Word版含解析)
文档属性
| 名称 | 2019-2020学年山东省威海市七年级上册期末数学试卷(五四学制)(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 23:35:01 | ||
图片预览




文档简介
2019-2020学年山东省威海市七年级上册期末数学试卷(五四学制)
题号
一
二
三
总分
得分
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
直线与x轴的交点坐标是
A.
B.
C.
D.
的平方根为
A.
B.
C.
D.
4
如果一个三角形的两条边长分别为2和6,那么这个三角形的第三边的长可能是
A.
2
B.
9
C.
4
D.
6
如图,中,,,AD平分,,于E,则
A.
1
B.
2
C.
3
D.
4
估计的值应该在?
?
?
?
A.
之间
B.
之间
C.
之间
D.
之间
将一副三角板按图所示的摆放,那么的度数等于
A.
B.
C.
D.
若点在第二象限,则m的值可能是
A.
1
B.
0
C.
D.
如图,在中,,,BD平分,则的度数为?
?
?
A.
B.
C.
D.
汽车油箱中有油,平均耗油量为如果不再加油,那么油箱中的油量单位:与行驶路程单位:的函数图象为
A.
B.
C.
D.
点关于y轴的对称点是
A.
B.
C.
D.
如图,中,,,,现将沿着DE折叠,使点B与点A重合,则的值是
A.
B.
C.
D.
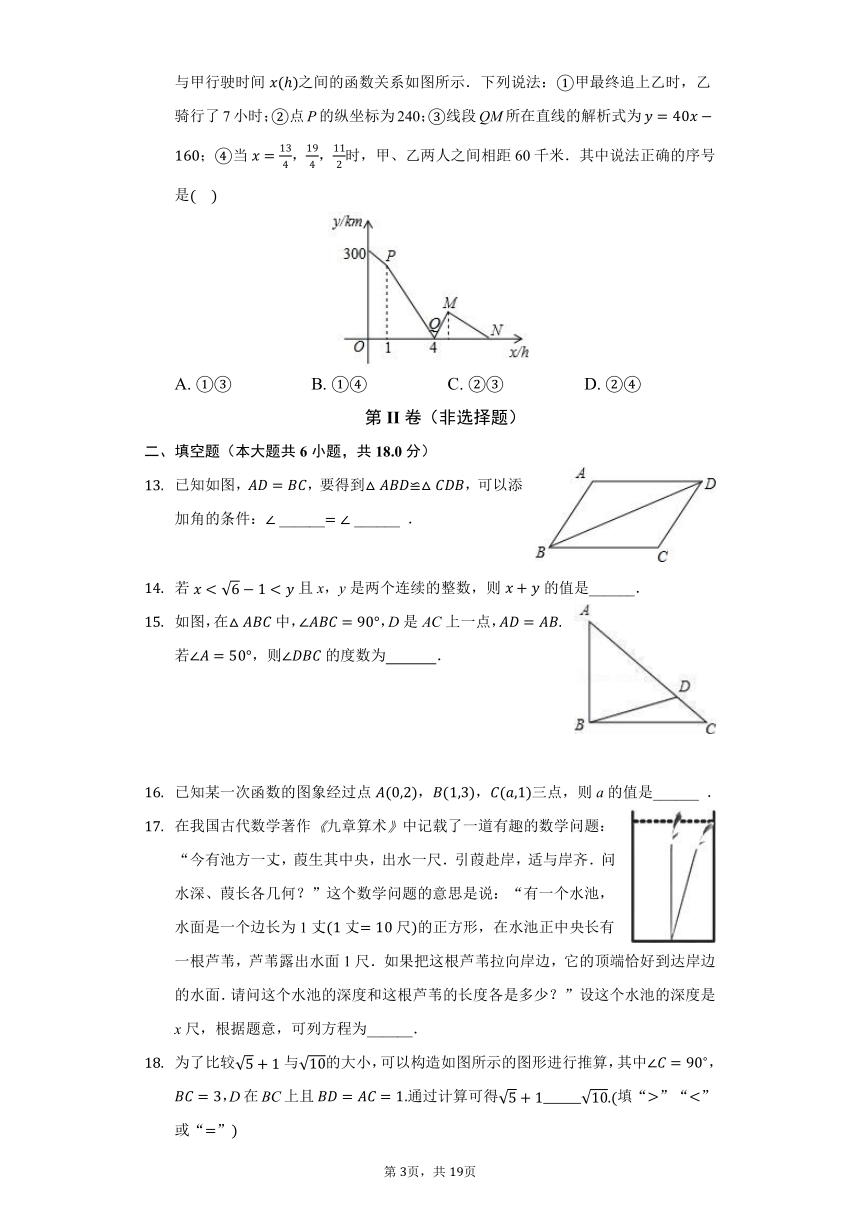
已知A,B两地相距300千米,甲骑摩托车从A地出发匀速驶向B地.当甲行驶1h后,乙骑自行车以的速度从B地出发匀速驶向A地,甲到达B地后马上以原速按原路返回,直至甲追上乙.在此过程中,甲、乙两人之间的距离与甲行驶时间之间的函数关系如图所示.下列说法:甲最终追上乙时,乙骑行了7小时;点P的纵坐标为240;线段QM所在直线的解析式为;当,,时,甲、乙两人之间相距60千米.其中说法正确的序号是
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共6小题,共18.0分)
已知如图,,要得到≌,可以添加角的条件:____________
.
若且x,y是两个连续的整数,则的值是______.
如图,在中,,D是AC上一点,若,则的度数为
???????????.
已知某一次函数的图象经过点,,三点,则a的值是______
.
在我国古代数学著作九章算术中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为1丈丈尺的正方形,在水池正中央长有一根芦苇,芦苇露出水面1?尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是x尺,根据题意,可列方程为______.
为了比较与的大小,可以构造如图所示的图形进行推算,其中,,D在BC上且通过计算可得??????????填“”“”或“”
三、解答题(本大题共7小题,共66.0分)
计算:
如图,在中,AD是的平分线,交BC于点D,CE是AB边上的高,若,,求的度数.
如图,已知,,AC和BD交于点O,E是AD的中点,连接OE.
求证:≌;
求的度数.
如图,在中,,,,,求的周长.
某产品每件的销售价x元与产品的日销售量y件之间的关系如下表:
若日销售量y是销售价x的一次函数.
求出日销售量y件与销售价x元的函数表达式;
若该产品每件成本10元,销售价定为30元时,求每日的销售利润.
如图,在平面直角坐标系中,已知点,点关于y轴对称的点分别是点C,点D.
请写出点C,点D的坐标;
在x轴上求作一点P,使的值最小保留作图痕迹,不要求写作法并直接写出点P的坐标.
如图,直线分别与x轴y轴交于B、A两点,直线AC交x轴于点C,且.
求的值;
求直线AC的解析式;
直线平行于直线AB,点D为第二象限内上的一点,连接AD,在x轴的正半轴上取一点E,使,点F为AC延长线上一点,且,延长DF交AE于点H,当时,连接DE,求的度数.
答案和解析
1.【答案】D
【解析】
【分析】
本题考查了一次函数图象上点的坐标特征,掌握直线与x轴的交点的纵坐标为0是本题的关键.
把代入即可求出直线与x轴的交点坐标.
【解答】
解:当时,,
,
即直线与x轴的交点坐标为,
故选:D.
2.【答案】C
【解析】解:,
又,
的平方根是.
故选:C.
首先根据立方根的定义化简,然后根据平方根的定义即可求出结果.
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
3.【答案】D
【解析】
【分析】
本题考查了三角形三边关系,此题实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.
根据在三角形中任意两边之和第三边,任意两边之差第三边;可求第三边长的范围,再选出答案.
【解答】
解:设第三边长为x,则
由三角形三边关系定理得,即,
故选D.
4.【答案】D
【解析】解:平分,,,
,
,
,
故选:D.
根据角平分线性质求出CD的长和的度数,根据含30度角的直角三角形性质求出BD即可.
本题考查了对含30度角的直角三角形的性质和角平分线性质的应用,求出DE的长是解此题的关键.
5.【答案】C
【解析】
【分析】
本题考查了估算无理数的大小的应用,解此题的关键是求出的范围先估算的范围,再估算的范围.
【解答】
解:,
,
故选C.
6.【答案】A
【解析】解:如图,
,,
,
故选A.
根据三角形的内角和和外角的性质即可得到结论.
本题考查了三角形的内角和,三角形的外角的性质,熟记各三角板各角的度数是解题的关键.
7.【答案】C
【解析】解:点在第二象限,
可得:,
解得:,
所以m的值可能是,
故选:C.
点在第二象限的条件是:横坐标是负数,纵坐标是正数.
此题考查点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.
8.【答案】D
【解析】
【分析】
本题主要考查的是直角三角形的性质,熟知在直角三角形中,两个锐角互余是解答此题的关键?
先根据直角三角形的性质求出的度数,由角平分线的定义求出的度数,根据三角形外角的性质即可得出结论.
【解答】
解:中,,,
.
平分,
,
.
?故选D.
9.【答案】B
【解析】
【分析】
本题考查的是一次函数的应用有关知识,根据题意列出函数关系式,然后再进行解答即可.
【解答】
解:由题意可得:,
自变量x的取值范围是:,
汽车行驶200km时,油箱中所剩的汽油为:.
故选B.
10.【答案】D
【解析】
【分析】
本题考查了轴对称中的坐标变化,根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变,即点关于y轴的对称点的坐标是.
【解答】
解:点,
关于y轴的对称点的坐标是.
故选D.
11.【答案】C
【解析】解:由题意知,
设,则,,
在中,由,得.
解得.
的长为,
,
.
故选:C.
由折叠易得,那么可用BE表示出CE长,那么就表示出了直角的三边,利用勾股定理即可求得BE长.
考查了翻折变换折叠问题,本题利用了:折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;直角三角形的勾股定理.
12.【答案】D
【解析】解:由图可知Q点为迎面相遇点,坐标为,从而此时甲走了4小时,乙走了3小时,则乙走了千米,甲走了千米,
甲的速度为:千米时,千米,
点P坐标为故正确,排除选项A、B;
由图象可知点M处甲到达终点,小时,千米,
故点M坐标为:;
设QM解析式为:,把点和代入得:
,
解得,
,
故错误.故排除C.
综上所述,只有D正确.
故选:D.
由图可知Q点为迎面相遇点;点M处甲到达终点.从而先求出相遇时乙走的路程,然后用全程300千米减去乙走的路程,得甲走的路程,再除以甲走的时间,从而得甲的速度,从而可知点P坐标,从而排除选项A和B,再求出QM的解析式,从而排除C,得正确答案为D.
本题主要考查一次函数的实际应用能力,根据题意弄清图象的实际意义是解题的基础和关键.分析出点Q点M为什么位置至关重要.
13.【答案】ADB;答案不唯一
【解析】解:可以添加:,
在和中,
,
≌,
故答案为ADB;答案不唯一.
可以添加条件:,再根据题目条件,再加上公共边,可利用SAS证明≌.
此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
14.【答案】3
【解析】解:,
,即,
,,
则,
故答案为:3
估算得出的范围,进而求出x与y的值,即可求出所求.
此题考查了估算无理数的大小,弄清估算的方法是解本题的关键.
15.【答案】
【解析】
【分析】
此题主要考查了等腰三角形的性质,关键是掌握等边对等角,三角形内角和为根据等边对等角可得,再利用的度数减去的度数即可.?
【解答】
解:,
,
,
,
故答案为.
16.【答案】
【解析】解:设一次函数的解析式为,
将点,分别代入解析式得,
,
解得,
则函数解析式为,
将代入解析式得,,
解得,
故答案为.
根据点,的坐标求出函数解析式,再将代入解析式求出a的值.
本题考查了一次函数图象上点的坐标特征,熟悉待定系数法是解题的关键.
17.【答案】
【解析】解:设水池的深度为x尺,水池正中央到岸边的距离为5尺,
由题意得:,
故答案为:.
首先设水池的深度为x尺,则这根芦苇的长度为尺,根据勾股定理可得方程.
此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
18.【答案】
【解析】
【分析】本题主要考查了三角形三边关系以及勾股定理的运用,解题时注意:三角形两边之和大于第三边先利用勾股定理求出AB和AD,再根据三角形的三边关系即可求解.
【解答】解:,,,,
,,
,
又ABD中,,
.
19.【答案】解:
【解析】首先计算乘方、开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
20.【答案】解:,,
,
是的平分线,
,
是AB边上的高,,
.
【解析】根据已知条件得到,根据角平分线的定义得到,根据三角形的内角和即可得到结论.
本题主要考查了三角形的内角和,熟练掌握三角形的内角和是解题的关键.
21.【答案】证明:在和中,
≌;
解:≌,
.
是AD的中点,
.
在和中,
≌.
.
,
.
【解析】此题考查了对全等三角形的判定和性质的掌握,要熟练掌握全等三角形的判定和性质是解题的关键,并能灵活运用.
由已知条件可以利用AAS来判定其全等;
根据≌得到,再由E是AD的中点,得到,证明≌,得到,又因为,即可得到.
22.【答案】解:,
.
在中,
,,
,
,.
在中,
,
,
,,
.
【解析】先根据题意得出,再由勾股定理得出AB的长,在中,根据直角三角形的性质得出AC及CD的长,进而可得出结论.
本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
23.【答案】解:设此一次函数关系式为,
则,
解得:,
故一次函数的关系式为:;
该产品每件成本10元,销售价定为30元时,
每件的利润为:元,
每日的销售利润为:元,
答:每日的销售利润为200元.
【解析】本题考查的是一次函数的应用有关知识.
利用日销售量y是销售价x的一次函数,进而利用待定系数法求一次函数解析式即可;
将已知代入求出销量每件利润,进而得出答案.
24.【答案】解:点C的坐标为,点D的坐标为
如图所示:
根据图形可知点P的坐标为.
【解析】本题主要考查的是轴对称图形的性质、轴对称--路径最短问题,掌握轴对称图形的性质是解题的关键.
关于y轴对称的两点的横坐标互为相反数,纵坐标相等;
首先求得点A关于x轴的对称点,连接交x轴于点P,此时的值最小.
25.【答案】解:直线,令,则,令,则,
即点A、B的坐标分别为、,
;
如图所示,在OA的延长线上取,
设:,则,
在中,设:,
则,,
,
解得:,
则点C坐标为;
过点D作轴交于点N,过点E作交于点K,
,,
,≌,
,,
,
设:,则,,
,,
点D坐标
直线平行于直线AB,直线OD的表达式为:,
将点D的坐标代入:,解得:,
故点,则点,
点
直线AD表达式中的k值为:,直线AE表达式中的k值为,
故:,而,
.
【解析】直线,令,则,令,则,即可求解;
如图所示,在OA的延长线上取,则,在中,设:,则,,即可求解;
证明≌,表示出点D坐标,即可求解.
本题考查的是一次函数综合运用,涉及到三角形全等、解直角三角形等知识点,其中,构建≌是本题的关键,题目难度很大.
第2页,共2页
第1页,共1页
题号
一
二
三
总分
得分
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
直线与x轴的交点坐标是
A.
B.
C.
D.
的平方根为
A.
B.
C.
D.
4
如果一个三角形的两条边长分别为2和6,那么这个三角形的第三边的长可能是
A.
2
B.
9
C.
4
D.
6
如图,中,,,AD平分,,于E,则
A.
1
B.
2
C.
3
D.
4
估计的值应该在?
?
?
?
A.
之间
B.
之间
C.
之间
D.
之间
将一副三角板按图所示的摆放,那么的度数等于
A.
B.
C.
D.
若点在第二象限,则m的值可能是
A.
1
B.
0
C.
D.
如图,在中,,,BD平分,则的度数为?
?
?
A.
B.
C.
D.
汽车油箱中有油,平均耗油量为如果不再加油,那么油箱中的油量单位:与行驶路程单位:的函数图象为
A.
B.
C.
D.
点关于y轴的对称点是
A.
B.
C.
D.
如图,中,,,,现将沿着DE折叠,使点B与点A重合,则的值是
A.
B.
C.
D.
已知A,B两地相距300千米,甲骑摩托车从A地出发匀速驶向B地.当甲行驶1h后,乙骑自行车以的速度从B地出发匀速驶向A地,甲到达B地后马上以原速按原路返回,直至甲追上乙.在此过程中,甲、乙两人之间的距离与甲行驶时间之间的函数关系如图所示.下列说法:甲最终追上乙时,乙骑行了7小时;点P的纵坐标为240;线段QM所在直线的解析式为;当,,时,甲、乙两人之间相距60千米.其中说法正确的序号是
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共6小题,共18.0分)
已知如图,,要得到≌,可以添加角的条件:____________
.
若且x,y是两个连续的整数,则的值是______.
如图,在中,,D是AC上一点,若,则的度数为
???????????.
已知某一次函数的图象经过点,,三点,则a的值是______
.
在我国古代数学著作九章算术中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为1丈丈尺的正方形,在水池正中央长有一根芦苇,芦苇露出水面1?尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是x尺,根据题意,可列方程为______.
为了比较与的大小,可以构造如图所示的图形进行推算,其中,,D在BC上且通过计算可得??????????填“”“”或“”
三、解答题(本大题共7小题,共66.0分)
计算:
如图,在中,AD是的平分线,交BC于点D,CE是AB边上的高,若,,求的度数.
如图,已知,,AC和BD交于点O,E是AD的中点,连接OE.
求证:≌;
求的度数.
如图,在中,,,,,求的周长.
某产品每件的销售价x元与产品的日销售量y件之间的关系如下表:
若日销售量y是销售价x的一次函数.
求出日销售量y件与销售价x元的函数表达式;
若该产品每件成本10元,销售价定为30元时,求每日的销售利润.
如图,在平面直角坐标系中,已知点,点关于y轴对称的点分别是点C,点D.
请写出点C,点D的坐标;
在x轴上求作一点P,使的值最小保留作图痕迹,不要求写作法并直接写出点P的坐标.
如图,直线分别与x轴y轴交于B、A两点,直线AC交x轴于点C,且.
求的值;
求直线AC的解析式;
直线平行于直线AB,点D为第二象限内上的一点,连接AD,在x轴的正半轴上取一点E,使,点F为AC延长线上一点,且,延长DF交AE于点H,当时,连接DE,求的度数.
答案和解析
1.【答案】D
【解析】
【分析】
本题考查了一次函数图象上点的坐标特征,掌握直线与x轴的交点的纵坐标为0是本题的关键.
把代入即可求出直线与x轴的交点坐标.
【解答】
解:当时,,
,
即直线与x轴的交点坐标为,
故选:D.
2.【答案】C
【解析】解:,
又,
的平方根是.
故选:C.
首先根据立方根的定义化简,然后根据平方根的定义即可求出结果.
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
3.【答案】D
【解析】
【分析】
本题考查了三角形三边关系,此题实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.
根据在三角形中任意两边之和第三边,任意两边之差第三边;可求第三边长的范围,再选出答案.
【解答】
解:设第三边长为x,则
由三角形三边关系定理得,即,
故选D.
4.【答案】D
【解析】解:平分,,,
,
,
,
故选:D.
根据角平分线性质求出CD的长和的度数,根据含30度角的直角三角形性质求出BD即可.
本题考查了对含30度角的直角三角形的性质和角平分线性质的应用,求出DE的长是解此题的关键.
5.【答案】C
【解析】
【分析】
本题考查了估算无理数的大小的应用,解此题的关键是求出的范围先估算的范围,再估算的范围.
【解答】
解:,
,
故选C.
6.【答案】A
【解析】解:如图,
,,
,
故选A.
根据三角形的内角和和外角的性质即可得到结论.
本题考查了三角形的内角和,三角形的外角的性质,熟记各三角板各角的度数是解题的关键.
7.【答案】C
【解析】解:点在第二象限,
可得:,
解得:,
所以m的值可能是,
故选:C.
点在第二象限的条件是:横坐标是负数,纵坐标是正数.
此题考查点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.
8.【答案】D
【解析】
【分析】
本题主要考查的是直角三角形的性质,熟知在直角三角形中,两个锐角互余是解答此题的关键?
先根据直角三角形的性质求出的度数,由角平分线的定义求出的度数,根据三角形外角的性质即可得出结论.
【解答】
解:中,,,
.
平分,
,
.
?故选D.
9.【答案】B
【解析】
【分析】
本题考查的是一次函数的应用有关知识,根据题意列出函数关系式,然后再进行解答即可.
【解答】
解:由题意可得:,
自变量x的取值范围是:,
汽车行驶200km时,油箱中所剩的汽油为:.
故选B.
10.【答案】D
【解析】
【分析】
本题考查了轴对称中的坐标变化,根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变,即点关于y轴的对称点的坐标是.
【解答】
解:点,
关于y轴的对称点的坐标是.
故选D.
11.【答案】C
【解析】解:由题意知,
设,则,,
在中,由,得.
解得.
的长为,
,
.
故选:C.
由折叠易得,那么可用BE表示出CE长,那么就表示出了直角的三边,利用勾股定理即可求得BE长.
考查了翻折变换折叠问题,本题利用了:折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;直角三角形的勾股定理.
12.【答案】D
【解析】解:由图可知Q点为迎面相遇点,坐标为,从而此时甲走了4小时,乙走了3小时,则乙走了千米,甲走了千米,
甲的速度为:千米时,千米,
点P坐标为故正确,排除选项A、B;
由图象可知点M处甲到达终点,小时,千米,
故点M坐标为:;
设QM解析式为:,把点和代入得:
,
解得,
,
故错误.故排除C.
综上所述,只有D正确.
故选:D.
由图可知Q点为迎面相遇点;点M处甲到达终点.从而先求出相遇时乙走的路程,然后用全程300千米减去乙走的路程,得甲走的路程,再除以甲走的时间,从而得甲的速度,从而可知点P坐标,从而排除选项A和B,再求出QM的解析式,从而排除C,得正确答案为D.
本题主要考查一次函数的实际应用能力,根据题意弄清图象的实际意义是解题的基础和关键.分析出点Q点M为什么位置至关重要.
13.【答案】ADB;答案不唯一
【解析】解:可以添加:,
在和中,
,
≌,
故答案为ADB;答案不唯一.
可以添加条件:,再根据题目条件,再加上公共边,可利用SAS证明≌.
此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
14.【答案】3
【解析】解:,
,即,
,,
则,
故答案为:3
估算得出的范围,进而求出x与y的值,即可求出所求.
此题考查了估算无理数的大小,弄清估算的方法是解本题的关键.
15.【答案】
【解析】
【分析】
此题主要考查了等腰三角形的性质,关键是掌握等边对等角,三角形内角和为根据等边对等角可得,再利用的度数减去的度数即可.?
【解答】
解:,
,
,
,
故答案为.
16.【答案】
【解析】解:设一次函数的解析式为,
将点,分别代入解析式得,
,
解得,
则函数解析式为,
将代入解析式得,,
解得,
故答案为.
根据点,的坐标求出函数解析式,再将代入解析式求出a的值.
本题考查了一次函数图象上点的坐标特征,熟悉待定系数法是解题的关键.
17.【答案】
【解析】解:设水池的深度为x尺,水池正中央到岸边的距离为5尺,
由题意得:,
故答案为:.
首先设水池的深度为x尺,则这根芦苇的长度为尺,根据勾股定理可得方程.
此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
18.【答案】
【解析】
【分析】本题主要考查了三角形三边关系以及勾股定理的运用,解题时注意:三角形两边之和大于第三边先利用勾股定理求出AB和AD,再根据三角形的三边关系即可求解.
【解答】解:,,,,
,,
,
又ABD中,,
.
19.【答案】解:
【解析】首先计算乘方、开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
20.【答案】解:,,
,
是的平分线,
,
是AB边上的高,,
.
【解析】根据已知条件得到,根据角平分线的定义得到,根据三角形的内角和即可得到结论.
本题主要考查了三角形的内角和,熟练掌握三角形的内角和是解题的关键.
21.【答案】证明:在和中,
≌;
解:≌,
.
是AD的中点,
.
在和中,
≌.
.
,
.
【解析】此题考查了对全等三角形的判定和性质的掌握,要熟练掌握全等三角形的判定和性质是解题的关键,并能灵活运用.
由已知条件可以利用AAS来判定其全等;
根据≌得到,再由E是AD的中点,得到,证明≌,得到,又因为,即可得到.
22.【答案】解:,
.
在中,
,,
,
,.
在中,
,
,
,,
.
【解析】先根据题意得出,再由勾股定理得出AB的长,在中,根据直角三角形的性质得出AC及CD的长,进而可得出结论.
本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
23.【答案】解:设此一次函数关系式为,
则,
解得:,
故一次函数的关系式为:;
该产品每件成本10元,销售价定为30元时,
每件的利润为:元,
每日的销售利润为:元,
答:每日的销售利润为200元.
【解析】本题考查的是一次函数的应用有关知识.
利用日销售量y是销售价x的一次函数,进而利用待定系数法求一次函数解析式即可;
将已知代入求出销量每件利润,进而得出答案.
24.【答案】解:点C的坐标为,点D的坐标为
如图所示:
根据图形可知点P的坐标为.
【解析】本题主要考查的是轴对称图形的性质、轴对称--路径最短问题,掌握轴对称图形的性质是解题的关键.
关于y轴对称的两点的横坐标互为相反数,纵坐标相等;
首先求得点A关于x轴的对称点,连接交x轴于点P,此时的值最小.
25.【答案】解:直线,令,则,令,则,
即点A、B的坐标分别为、,
;
如图所示,在OA的延长线上取,
设:,则,
在中,设:,
则,,
,
解得:,
则点C坐标为;
过点D作轴交于点N,过点E作交于点K,
,,
,≌,
,,
,
设:,则,,
,,
点D坐标
直线平行于直线AB,直线OD的表达式为:,
将点D的坐标代入:,解得:,
故点,则点,
点
直线AD表达式中的k值为:,直线AE表达式中的k值为,
故:,而,
.
【解析】直线,令,则,令,则,即可求解;
如图所示,在OA的延长线上取,则,在中,设:,则,,即可求解;
证明≌,表示出点D坐标,即可求解.
本题考查的是一次函数综合运用,涉及到三角形全等、解直角三角形等知识点,其中,构建≌是本题的关键,题目难度很大.
第2页,共2页
第1页,共1页
同课章节目录
