四年级下册数学课件 4.3 三角形的内角和 青岛版 (共23张PPT)
文档属性
| 名称 | 四年级下册数学课件 4.3 三角形的内角和 青岛版 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 703.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:13:19 | ||
图片预览





文档简介
(共23张PPT)
三角形的内角和
形状像座山,稳定性能坚。
三根首尾连,学问不简单。
同学们,你们知道是什么图形吗?
猜谜语
三角形三个内角的度数和
叫做三角形的内角和。
∠1+∠2+∠3
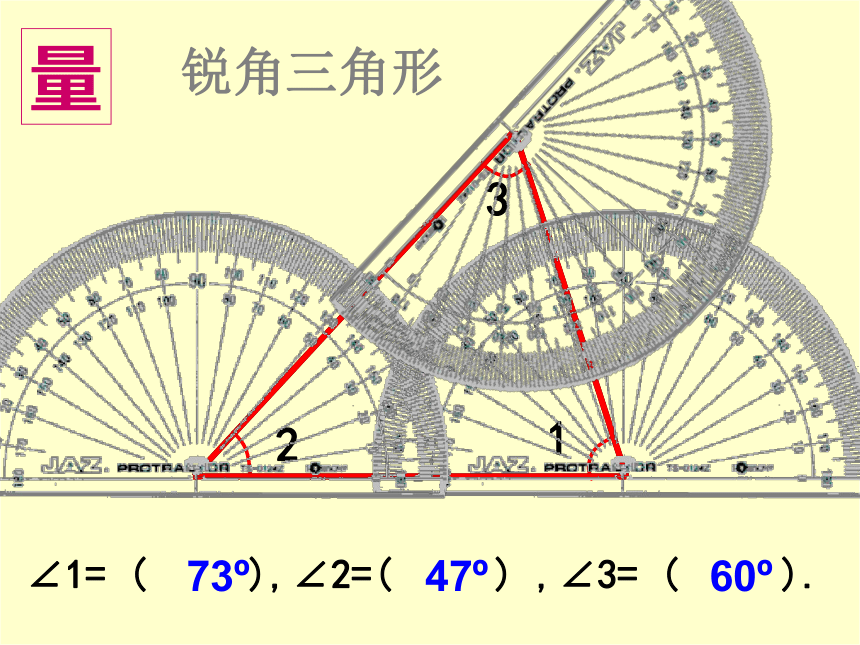
锐角三角形
量
2
1
3
∠1=
(
),∠2=(
)
,∠3=
(
).
73?
47?
60?
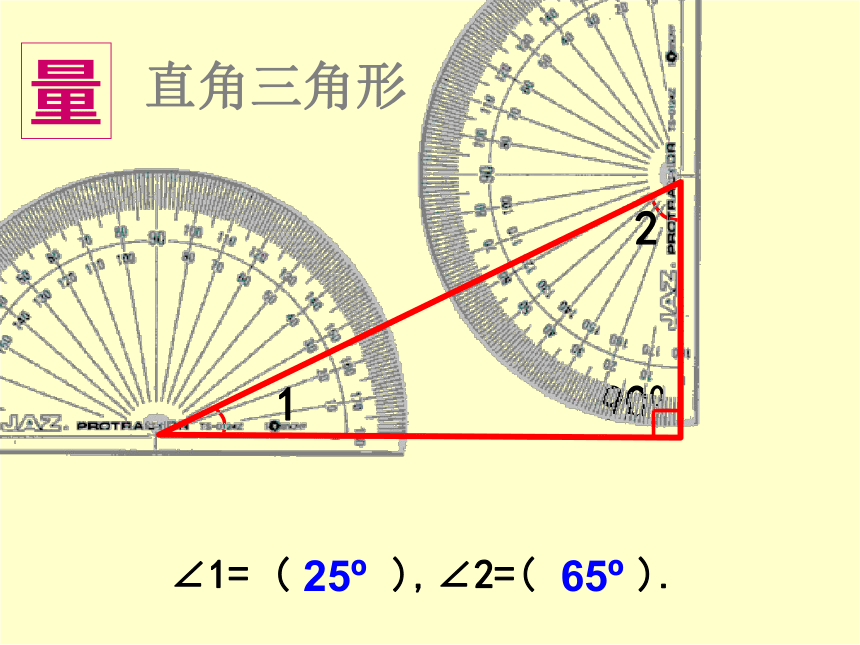
直角三角形
1
900
2
量
∠1=
(
),∠2=(
).
25?
65?
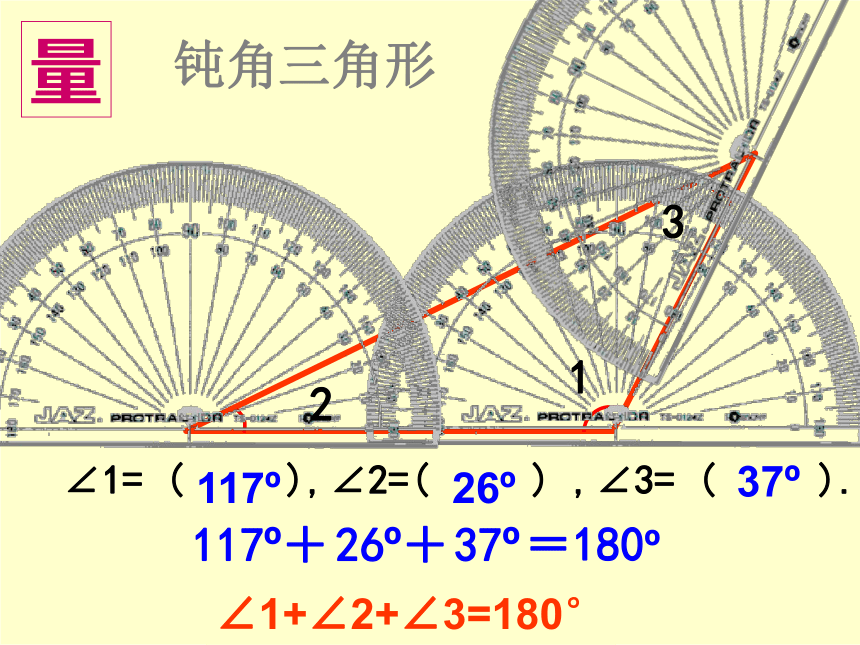
钝角三角形
2
1
3
量
∠1=
(
),∠2=(
)
,∠3=
(
).
117?
26?
37?
117?+
26?+
37?
=180?
∠1+∠2+∠3=180°
3
2
3
1
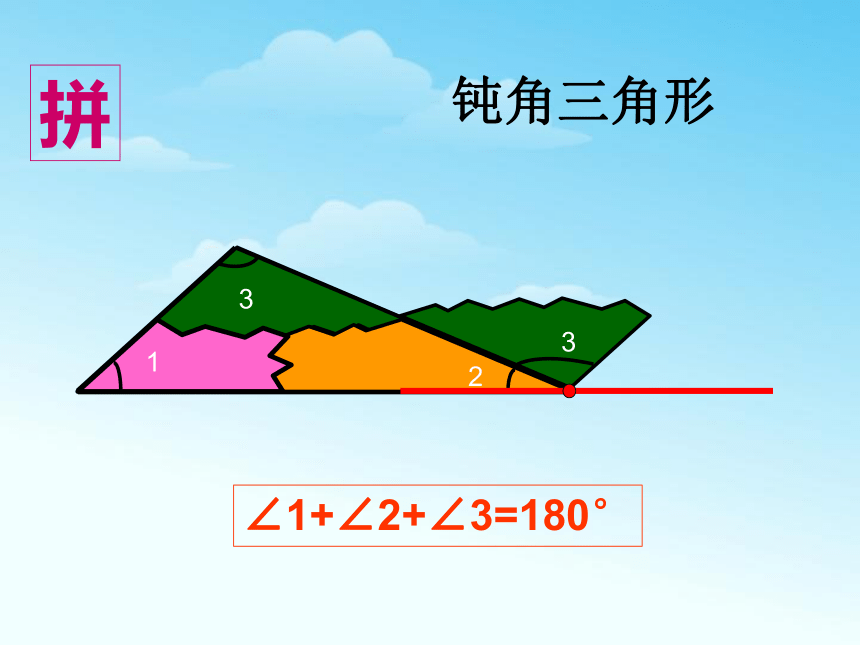
拼
∠1+∠2+∠3=180°
锐角三角形
∠1+∠2+∠3=180°
拼
2
1
3
3
直角三角形
拼
3
2
1
3
∠1+∠2+∠3=180°
钝角三角形
1
1
2
2
3
3
折
锐角三角形
折
直角三角形
1
1
2
2
3
3
折
钝角三角形
三角形的内角和是180°
结论:
帕斯卡(BlaisePascal,1623~1662)
,法国数学家、物理学家、近代概率论的奠基者。早在300多年前这位法国著名的科学家就已经发现了任何三角形的内角和是180°,而他当时才12岁。
三角形的内角和
做一做
:
(课本:67页)在一个三角形中,已知:∠1=140°,
∠3=25°,
求
:∠2的度数。
提高练习
如图,在等腰三角形中,其中底角∠1=70?,则顶角
∠2=(
).
40°
180?
-
70?
×2
=180?
-140?
=40?
2
3
1
(1)锐角三角形的内角和小于钝角三角形的内角和。
(
)
(2)把一个三角形分成2个三角形,每个三角形的内角和是90度。
(
)
(3)一个三角形里可能有2个钝角,也可能有2个直角。
(
)
我是小法官
长方形的内角和是多少度?
五
边
形
六
边
形
这节课你有哪些收获?
任意三角形的内角和是180°
结论:
课后作业:
课本:69页第1、2、3题
本节结束,同学们再见!
三角形的内角和
形状像座山,稳定性能坚。
三根首尾连,学问不简单。
同学们,你们知道是什么图形吗?
猜谜语
三角形三个内角的度数和
叫做三角形的内角和。
∠1+∠2+∠3
锐角三角形
量
2
1
3
∠1=
(
),∠2=(
)
,∠3=
(
).
73?
47?
60?
直角三角形
1
900
2
量
∠1=
(
),∠2=(
).
25?
65?
钝角三角形
2
1
3
量
∠1=
(
),∠2=(
)
,∠3=
(
).
117?
26?
37?
117?+
26?+
37?
=180?
∠1+∠2+∠3=180°
3
2
3
1
拼
∠1+∠2+∠3=180°
锐角三角形
∠1+∠2+∠3=180°
拼
2
1
3
3
直角三角形
拼
3
2
1
3
∠1+∠2+∠3=180°
钝角三角形
1
1
2
2
3
3
折
锐角三角形
折
直角三角形
1
1
2
2
3
3
折
钝角三角形
三角形的内角和是180°
结论:
帕斯卡(BlaisePascal,1623~1662)
,法国数学家、物理学家、近代概率论的奠基者。早在300多年前这位法国著名的科学家就已经发现了任何三角形的内角和是180°,而他当时才12岁。
三角形的内角和
做一做
:
(课本:67页)在一个三角形中,已知:∠1=140°,
∠3=25°,
求
:∠2的度数。
提高练习
如图,在等腰三角形中,其中底角∠1=70?,则顶角
∠2=(
).
40°
180?
-
70?
×2
=180?
-140?
=40?
2
3
1
(1)锐角三角形的内角和小于钝角三角形的内角和。
(
)
(2)把一个三角形分成2个三角形,每个三角形的内角和是90度。
(
)
(3)一个三角形里可能有2个钝角,也可能有2个直角。
(
)
我是小法官
长方形的内角和是多少度?
五
边
形
六
边
形
这节课你有哪些收获?
任意三角形的内角和是180°
结论:
课后作业:
课本:69页第1、2、3题
本节结束,同学们再见!
