人教版数学选修1-2 1.2独立性检验的基本思想及其初步应用(30张PPT)
文档属性
| 名称 | 人教版数学选修1-2 1.2独立性检验的基本思想及其初步应用(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览






文档简介
(共30张PPT)
1.2独立性检验的基本思想及其初步应用
独立性检验
对于性别变量,其取值为男和女两种。这种变量的不同‘值’
,表示个体所属的不同类别,像这样的变量称为分类变量
在日常生活中,我们常常关心分类变量之间是否有关系:
例如,吸烟是否与患肺癌有关系?
性别是否对于喜欢数学课程有影响?等等。
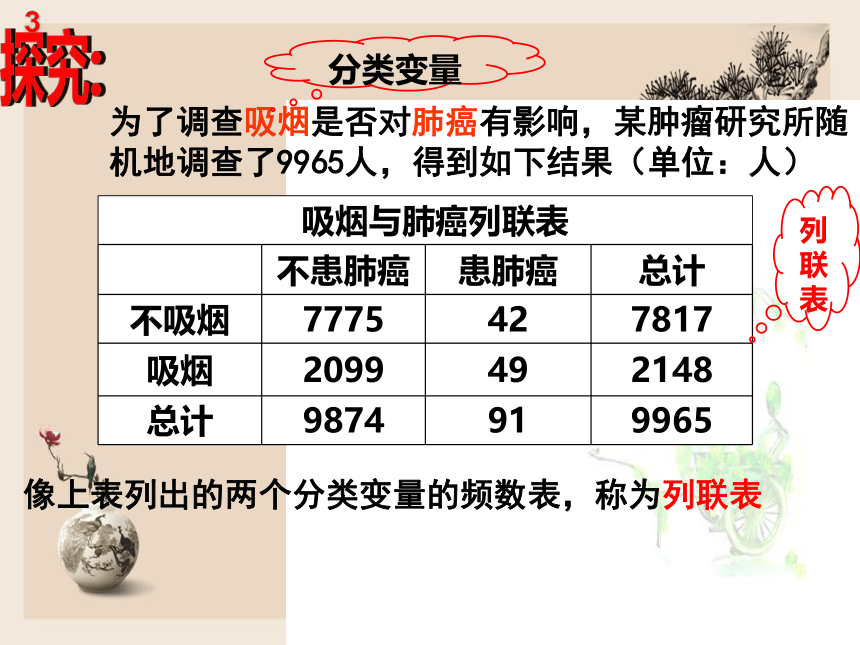
吸烟与肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)
列联表
分类变量
像上表列出的两个分类变量的频数表,称为列联表
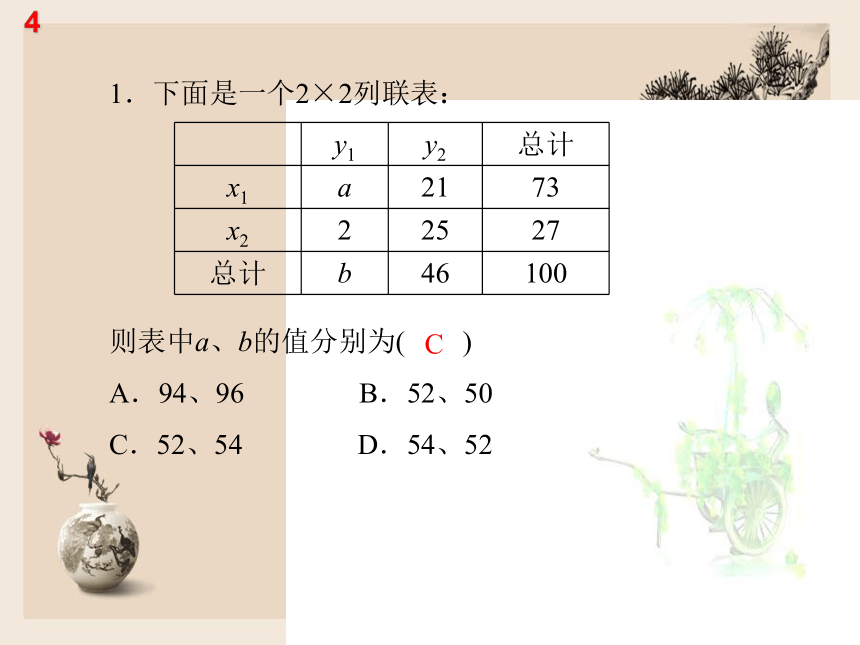
1.下面是一个2×2列联表:
y1
y2
总计
x1
a
21
73
x2
2
25
27
总计
b
46
100
则表中a、b的值分别为( )
A.94、96
B.52、50
C.52、54
D.54、52
C
吸烟与肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
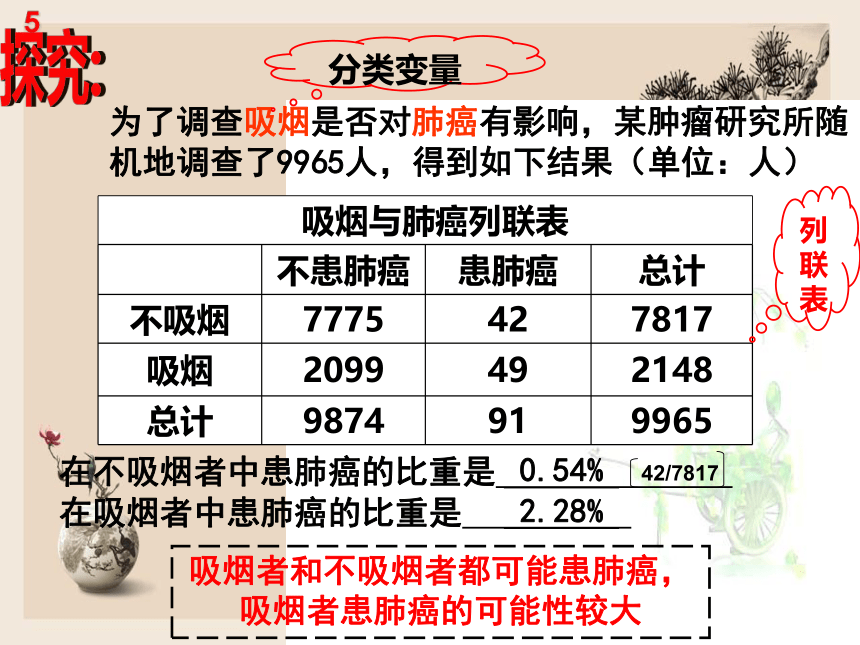
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)
列联表
在不吸烟者中患肺癌的比重是
在吸烟者中患肺癌的比重是
吸烟者和不吸烟者都可能患肺癌,吸烟者患肺癌的可能性较大
0.54%
2.28%
分类变量
42/7817
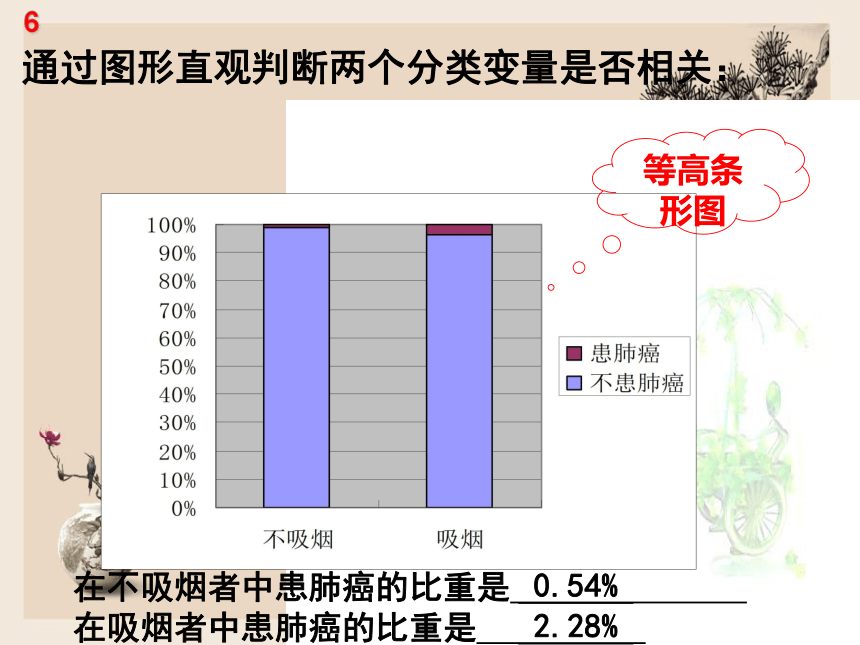
通过图形直观判断两个分类变量是否相关:
等高条形图
在不吸烟者中患肺癌的比重是
在吸烟者中患肺癌的比重是
0.54%
2.28%
上面我们通过分析数据和图形,得到的直观印象是吸烟和患肺癌有关,那么事实是否真的如此呢?这需要用统计观点来考察这个问题。
现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,
为此先假设
H0:吸烟与患肺癌没有关系.
不患肺癌
患肺癌
总计
不吸烟
a
b
a+b
吸烟
c
d
c+d
总计
a+c
b+d
n=a+b+c+d
独立性检验
在不吸烟者中不患肺癌的比重是
在吸烟者中不患肺癌的比重是
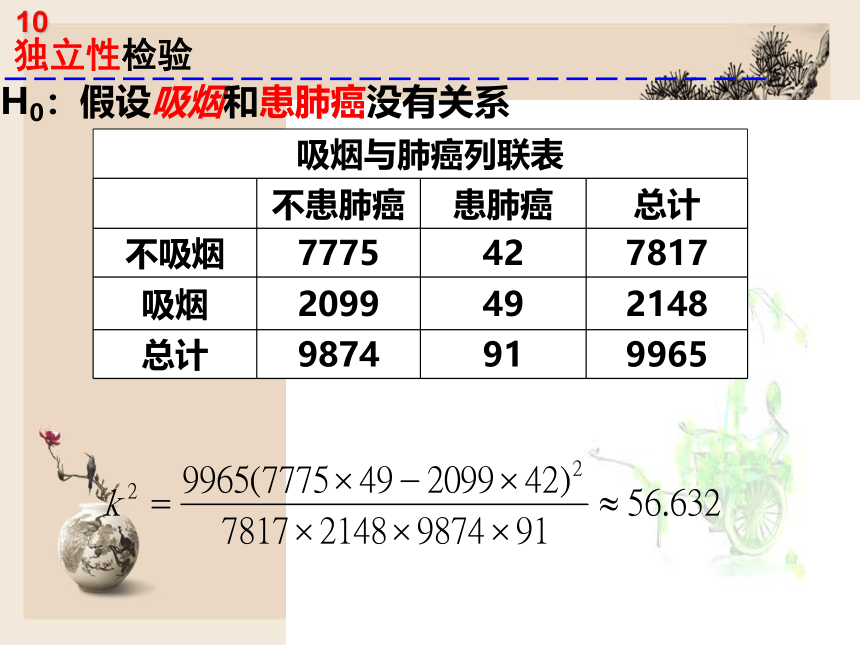
H0:假设吸烟和患肺癌没有关系
独立性检验
H0:假设吸烟和患肺癌没有关系
构造随机变量(卡方统计量)
作为检验在多大程度上可以认为“两个变量有关系”的标准
。
若H0(吸烟和患肺癌没有关系)成立,则K2应该很小.
独立性检验
H0:假设吸烟和患肺癌没有关系
吸烟与肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
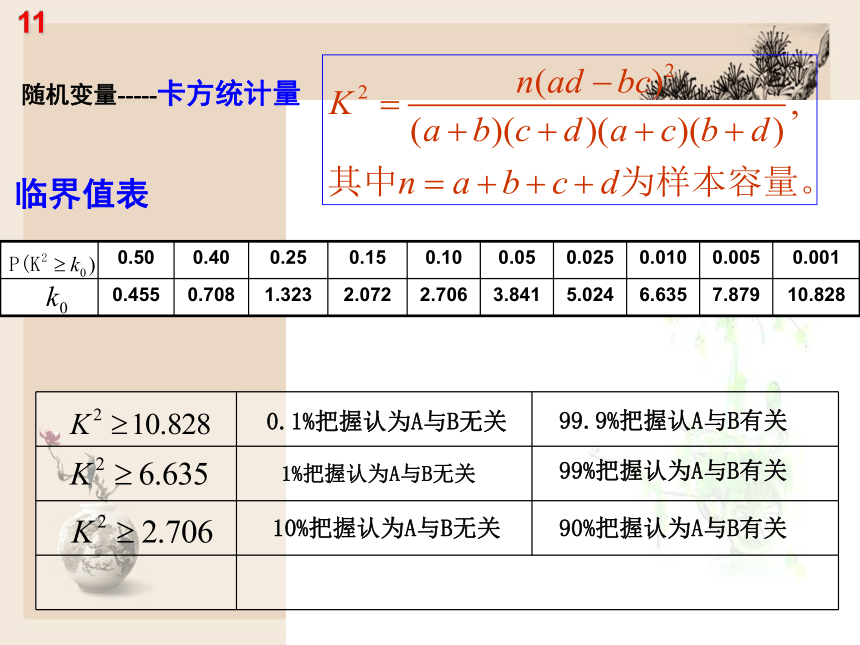
随机变量-----卡方统计量
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
临界值表
0.1%把握认为A与B无关
1%把握认为A与B无关
99.9%把握认A与B有关
99%把握认为A与B有关
90%把握认为A与B有关
10%把握认为A与B无关
即在
成立的情况下,K2
大于6.635概率非常小,近似为0.01
现在的K2≈56.632的观测值远大于6.635,小概率事件的发生说明假设H0不成立!
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
临界值表
独立性检验
H0:假设吸烟和患肺癌没有关系
所以吸烟和患肺癌有关!
1.对分类变量X与Y的随机变量K2的观测值k,说法正确的是( )
A.k越大,“
X与Y有关系”可信程度越小
B.k越小,“
X与Y有关系”可信程度越小
C.k越接近于0,“X与Y无关”程度越小
D.k越大,“X与Y无关”程度越大
B
独立性检验基本的思想类似反证法
(1)假设结论不成立,即“两个分类变量没有关系”.
(2)在此假设下随机变量
K2
应该很能小,如果由观测数据计算得到K2的观测值k很大,则在一定程度上说明假设不合理.
(3)根据随机变量K2的含义,可以通过评价该假设不合理的程度,由实际计算出的,说明假设合理的程度为99.9%,即“两个分类变量有关系”这一结论成立的可信度为约为99.9%.
反证法原理与假设检验原理
反证法原理:
在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立。
假设检验原理:在一个已知假设下,如果一个与该假设矛盾的小概率事件发生,就推断这个假设不成立。
在H0成立的条件下,构造与H0矛盾的小概率事件;
2.如果样本使得这个小概率事件发生,则H0不成立,就能以一定把握断言H1成立;否则,断言没有发现样本数据与H0相矛盾的证据。
求解思路
假设检验问题:
例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?
患心脏病
不患心脏病
总计
秃顶
214
175
389
不秃顶
451
597
1048
总计
665
772
1437
在秃顶中患心脏病的比重是
在不秃顶中患心脏病的比重是
55.01%
43.03%
例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?
患心脏病
不患心脏病
总计
秃顶
214
175
389
不秃顶
451
597
1048
总计
665
772
1437
根据联表的数据,得到
所以有99%的把握认为“秃顶与患心脏病有关”。
注意:
因为这组数据来自住院的病人,因此所得到的结论适合住院的病人群体.
2、本例中的边框中的注解:
1、在解决实际问题时,可以直接计算K2的观测值k进行独立检验,而不必写出K2的推导过程;
主要是使得我们注意统计结果的适用范围(这由样本的代表性所决定)
A
所以根据列联表的数据,可以有
%的把握认为该学校15至16周岁的男生的身高和体重之间有关系。
97.5
由独立性检验随机变量
值的计算公式得:
跟踪训练
1.(2011·广东执信中学)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)能否在犯错误的概率不超过0.001的前提下认为学生的积极性与对待班级工作的态度有关系?
所以,在犯错误的概率不超过0.001的前提下,认为“学生的学习积极性与对待班级工作的态度”有关系.
2.(2011·揭阳一模)某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量/克
频数
(490,495]
6
(495,500]
8
(500,505]
14
(505,510]
8
(510,515]
4
表1 甲流水线样本频数分布表
(1)根据上表数据作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面2×2列联表,能否在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关?
甲流水线
乙流水线
合计
合格品
a=
b=
不合格品
c=
d=
合计
n=
附:下面的临界值表供参考:
p(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
解析:(1)甲流水线样本的频率分布直方图如下:
(2)由表1知甲样本中合格品数为8+14+8=30,由图1知乙样本中合格品数为(0.06+0.09+0.03)×5×40=36,故甲样本合格品的频率为
=0.75,
乙样本合格品的频率为
=0.9,
据此可估计从甲流水线任取1件产品,该产品恰好是合格品的概率为0.75.从乙流水线任取1件产品,该产品恰好是合格品的概率为0.9.
(3)2×2列联表如下:
甲流水线
乙流水线
合计
合格品
a=30
b=36
66
不合格品
c=10
d=4
14
合计
40
40
n=80
∴在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关.
1.2独立性检验的基本思想及其初步应用
独立性检验
对于性别变量,其取值为男和女两种。这种变量的不同‘值’
,表示个体所属的不同类别,像这样的变量称为分类变量
在日常生活中,我们常常关心分类变量之间是否有关系:
例如,吸烟是否与患肺癌有关系?
性别是否对于喜欢数学课程有影响?等等。
吸烟与肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)
列联表
分类变量
像上表列出的两个分类变量的频数表,称为列联表
1.下面是一个2×2列联表:
y1
y2
总计
x1
a
21
73
x2
2
25
27
总计
b
46
100
则表中a、b的值分别为( )
A.94、96
B.52、50
C.52、54
D.54、52
C
吸烟与肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
为了调查吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)
列联表
在不吸烟者中患肺癌的比重是
在吸烟者中患肺癌的比重是
吸烟者和不吸烟者都可能患肺癌,吸烟者患肺癌的可能性较大
0.54%
2.28%
分类变量
42/7817
通过图形直观判断两个分类变量是否相关:
等高条形图
在不吸烟者中患肺癌的比重是
在吸烟者中患肺癌的比重是
0.54%
2.28%
上面我们通过分析数据和图形,得到的直观印象是吸烟和患肺癌有关,那么事实是否真的如此呢?这需要用统计观点来考察这个问题。
现在想要知道能够以多大的把握认为“吸烟与患肺癌有关”,
为此先假设
H0:吸烟与患肺癌没有关系.
不患肺癌
患肺癌
总计
不吸烟
a
b
a+b
吸烟
c
d
c+d
总计
a+c
b+d
n=a+b+c+d
独立性检验
在不吸烟者中不患肺癌的比重是
在吸烟者中不患肺癌的比重是
H0:假设吸烟和患肺癌没有关系
独立性检验
H0:假设吸烟和患肺癌没有关系
构造随机变量(卡方统计量)
作为检验在多大程度上可以认为“两个变量有关系”的标准
。
若H0(吸烟和患肺癌没有关系)成立,则K2应该很小.
独立性检验
H0:假设吸烟和患肺癌没有关系
吸烟与肺癌列联表
不患肺癌
患肺癌
总计
不吸烟
7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
随机变量-----卡方统计量
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
临界值表
0.1%把握认为A与B无关
1%把握认为A与B无关
99.9%把握认A与B有关
99%把握认为A与B有关
90%把握认为A与B有关
10%把握认为A与B无关
即在
成立的情况下,K2
大于6.635概率非常小,近似为0.01
现在的K2≈56.632的观测值远大于6.635,小概率事件的发生说明假设H0不成立!
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
临界值表
独立性检验
H0:假设吸烟和患肺癌没有关系
所以吸烟和患肺癌有关!
1.对分类变量X与Y的随机变量K2的观测值k,说法正确的是( )
A.k越大,“
X与Y有关系”可信程度越小
B.k越小,“
X与Y有关系”可信程度越小
C.k越接近于0,“X与Y无关”程度越小
D.k越大,“X与Y无关”程度越大
B
独立性检验基本的思想类似反证法
(1)假设结论不成立,即“两个分类变量没有关系”.
(2)在此假设下随机变量
K2
应该很能小,如果由观测数据计算得到K2的观测值k很大,则在一定程度上说明假设不合理.
(3)根据随机变量K2的含义,可以通过评价该假设不合理的程度,由实际计算出的,说明假设合理的程度为99.9%,即“两个分类变量有关系”这一结论成立的可信度为约为99.9%.
反证法原理与假设检验原理
反证法原理:
在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立。
假设检验原理:在一个已知假设下,如果一个与该假设矛盾的小概率事件发生,就推断这个假设不成立。
在H0成立的条件下,构造与H0矛盾的小概率事件;
2.如果样本使得这个小概率事件发生,则H0不成立,就能以一定把握断言H1成立;否则,断言没有发现样本数据与H0相矛盾的证据。
求解思路
假设检验问题:
例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?
患心脏病
不患心脏病
总计
秃顶
214
175
389
不秃顶
451
597
1048
总计
665
772
1437
在秃顶中患心脏病的比重是
在不秃顶中患心脏病的比重是
55.01%
43.03%
例1.在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.分别利用图形和独立性检验方法判断是否有关?你所得的结论在什么范围内有效?
患心脏病
不患心脏病
总计
秃顶
214
175
389
不秃顶
451
597
1048
总计
665
772
1437
根据联表的数据,得到
所以有99%的把握认为“秃顶与患心脏病有关”。
注意:
因为这组数据来自住院的病人,因此所得到的结论适合住院的病人群体.
2、本例中的边框中的注解:
1、在解决实际问题时,可以直接计算K2的观测值k进行独立检验,而不必写出K2的推导过程;
主要是使得我们注意统计结果的适用范围(这由样本的代表性所决定)
A
所以根据列联表的数据,可以有
%的把握认为该学校15至16周岁的男生的身高和体重之间有关系。
97.5
由独立性检验随机变量
值的计算公式得:
跟踪训练
1.(2011·广东执信中学)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)能否在犯错误的概率不超过0.001的前提下认为学生的积极性与对待班级工作的态度有关系?
所以,在犯错误的概率不超过0.001的前提下,认为“学生的学习积极性与对待班级工作的态度”有关系.
2.(2011·揭阳一模)某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量/克
频数
(490,495]
6
(495,500]
8
(500,505]
14
(505,510]
8
(510,515]
4
表1 甲流水线样本频数分布表
(1)根据上表数据作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面2×2列联表,能否在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关?
甲流水线
乙流水线
合计
合格品
a=
b=
不合格品
c=
d=
合计
n=
附:下面的临界值表供参考:
p(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
解析:(1)甲流水线样本的频率分布直方图如下:
(2)由表1知甲样本中合格品数为8+14+8=30,由图1知乙样本中合格品数为(0.06+0.09+0.03)×5×40=36,故甲样本合格品的频率为
=0.75,
乙样本合格品的频率为
=0.9,
据此可估计从甲流水线任取1件产品,该产品恰好是合格品的概率为0.75.从乙流水线任取1件产品,该产品恰好是合格品的概率为0.9.
(3)2×2列联表如下:
甲流水线
乙流水线
合计
合格品
a=30
b=36
66
不合格品
c=10
d=4
14
合计
40
40
n=80
∴在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关.
