2020-2021学年黑龙江省哈尔滨市南岗区八年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市南岗区八年级(上)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 788.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 05:46:50 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市南岗区八年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.(3分)下列方程中,是分式方程的是( )
A.+=1 B.x+=2 C.2x=x﹣5 D.x﹣4y=1
2.(3分)下列图案中不是轴对称图形的是( )
A. B.
C. D.
3.(3分)下列运算中,正确的是( )
A.a2?a3=a5 B.(a2)3=a5 C.a6÷a2=a3 D.a6﹣a2=a4
4.(3分)若分式的值为0,则x的值是( )
A.1或﹣1 B.1 C.﹣1 D.0
5.(3分)计算3a(5a﹣2b)的结果是( )
A.15a﹣6ab B.8a2﹣6ab C.15a2﹣5ab D.15a2﹣6ab
6.(3分)下列计算正确的是( )
A.﹣= B.= C.= D.﹣=6
7.(3分)计算(﹣3)0﹣2﹣3的结果是( )
A.﹣ B. C.6 D.7
8.(3分)若a≠b,则下列分式化简正确的是( )
A. B. C.= D.=
9.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
10.(3分)若的整数部分为x,小数部分为y,则x﹣y的值是( )
A.1 B. C.3﹣3 D.3
二、填空题(共10小题).
11.(3分)0.0012用科学记数法表示为 .
12.(3分)若分式有意义,则字母x满足的条件是 .
13.(3分)把多项式a3b﹣ab分解因式的结果为 .
14.(3分)计算﹣的结果是 .
15.(3分)计算:28x4y2÷7x3y= .
16.(3分)一个长方形的长和面积分别是和4,则这个长方形的宽为 .
17.(3分)等腰三角形的一个角是80°,则它的底角是 .
18.(3分)如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 .
19.(3分)当x=2时,代数式÷(x﹣1)的值为 .
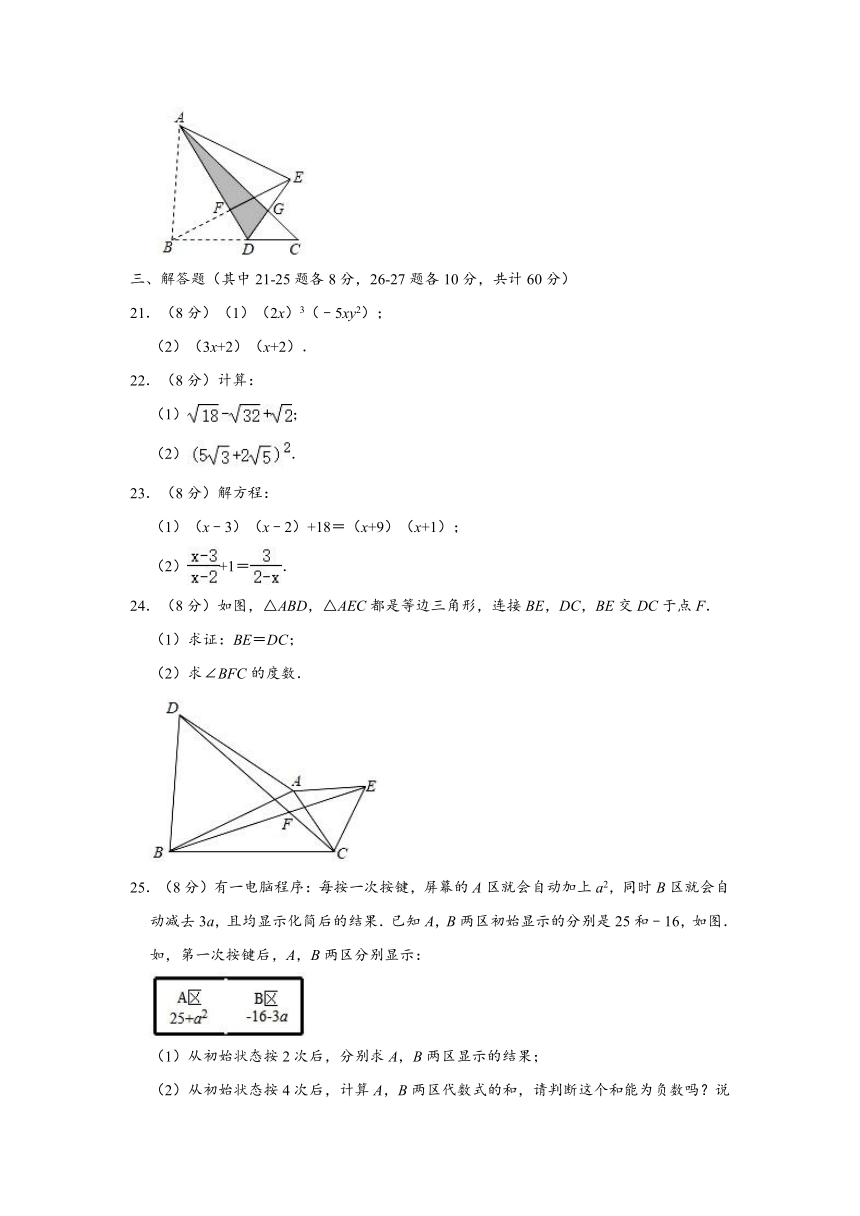
20.(3分)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则DF的长为 .
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
22.(8分)计算:
(1);
(2).
23.(8分)解方程:
(1)(x﹣3)(x﹣2)+18=(x+9)(x+1);
(2)+1=.
24.(8分)如图,△ABD,△AEC都是等边三角形,连接BE,DC,BE交DC于点F.
(1)求证:BE=DC;
(2)求∠BFC的度数.
25.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.
如,第一次按键后,A,B两区分别显示:
(1)从初始状态按2次后,分别求A,B两区显示的结果;
(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.
26.(10分)某商店想购进A、B两种商品,已知每件B种商品的进价比每件A种商品的进价多5元,且用300元购进A种商品的数量是用100元购进B种商品数量的4倍.
(1)求每件A种商品和每件B种商品的进价分别是多少元?
(2)商店决定购进A、B两种商品共50件,A种商品加价5元出售,B种商品比进价提高20%后出售,要使所有商品全部出售后利润不少于210元,求A种商品至少购进多少件?
27.(10分)已知:在△ABC中,AB=AC,点D在BA的延长线上,DE∥AC交BC的延长线于点E.
(1)如图1,求证:DB=DE;
(2)如图2,作△DBE的高EF,连接AE,若∠DEA=∠FEA,求证:∠AEB=45°;
(3)如图3,在(2)的条件下,过点B作BG⊥AE于点G,BG交AC于点H,若CE=4,且四边形CEGH的面积是24,求BH的长.
参考答案
一、选择题(每小题3分,共计30分)
1.(3分)下列方程中,是分式方程的是( )
A.+=1 B.x+=2 C.2x=x﹣5 D.x﹣4y=1
解:A、该方程是一元一次方程,故本选项不符合题意;
B、该方程符合分式方程的定义,故本选项符合题意;
C、该方程是一元一次方程,故本选项不符合题意;
D、该方程是二元一次方程,故本选项不符合题意;
故选:B.
2.(3分)下列图案中不是轴对称图形的是( )
A. B.
C. D.
解:A、是轴对称图形,故本选项不合题意;
B、是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项符合题意;
D、是轴对称图形,故本选项不合题意;
故选:C.
3.(3分)下列运算中,正确的是( )
A.a2?a3=a5 B.(a2)3=a5 C.a6÷a2=a3 D.a6﹣a2=a4
解:A、a2?a3=a2+3=a5,本选项正确;
B、(a2)3=a6,本选项错误;
C、a6÷a2=a6﹣2=a4,本选项错误;
D、a6与﹣a2不是同类项,不能合并,本选项错误;
故选:A.
4.(3分)若分式的值为0,则x的值是( )
A.1或﹣1 B.1 C.﹣1 D.0
解:根据题意知,x﹣1=0,
解得x=1.
故选:B.
5.(3分)计算3a(5a﹣2b)的结果是( )
A.15a﹣6ab B.8a2﹣6ab C.15a2﹣5ab D.15a2﹣6ab
解:3a(5a﹣2b)=15a2﹣6ab.
故选:D.
6.(3分)下列计算正确的是( )
A.﹣= B.= C.= D.﹣=6
解:A、原式=2﹣,所以A选项错误;
B、原式=2+3=5,所以B选项错误;
C、原式=,所以C选项正确;
D、原式=5﹣=4,所以D选项错误.
故选:C.
7.(3分)计算(﹣3)0﹣2﹣3的结果是( )
A.﹣ B. C.6 D.7
解:原式=1﹣
=.
故选:B.
8.(3分)若a≠b,则下列分式化简正确的是( )
A. B. C.= D.=
解:∵a≠b,
∴,故选项A错误;
,故选项B错误;
≠,故选项C错误;
=,故选项D正确;
故选:D.
9.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
解:由作图知,MN是线段BC的垂直平分线,
∴BD=CD,
∵AC=6,AD=2,
∴BD=CD=4,
故选:C.
10.(3分)若的整数部分为x,小数部分为y,则x﹣y的值是( )
A.1 B. C.3﹣3 D.3
解:∵1,
∴x=1,y=﹣1,
∴x﹣y=×1﹣(﹣1)=1,
故选:A.
二、填空题(每小题3分,共计30分)
11.(3分)0.0012用科学记数法表示为 1.2×10﹣3 .
解:将0.0012用科学记数法表示为1.2×10﹣3,
故答案是:1.2×10﹣3.
12.(3分)若分式有意义,则字母x满足的条件是 x≠0 .
解:由题意得:3x≠0,
解得x≠0.
故答案为:x≠0.
13.(3分)把多项式a3b﹣ab分解因式的结果为 ab(a+1)(a﹣l) .
解:a3b﹣ab
=ab(a2﹣1)
=ab(a+1)(a﹣1).
故答案为ab(a+1)(a﹣1).
14.(3分)计算﹣的结果是 .
解:原式=4﹣3
=,
故答案为:.
15.(3分)计算:28x4y2÷7x3y= 4xy .
解:28x4y2÷7x3y=4xy,
故答案为:4xy.
16.(3分)一个长方形的长和面积分别是和4,则这个长方形的宽为 2 .
解:由题意知:长方形的宽为:===2,
故答案为:2.
17.(3分)等腰三角形的一个角是80°,则它的底角是 50°或80° .
解:由题意知,分两种情况:
(1)当这个80°的角为顶角时,则底角=(180°﹣80°)÷2=50°;
(2)当这个80°的角为底角时,则另一底角也为80°.
故答案为:50°或80°.
18.(3分)如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 10° .
解:∵∠B=50°,∠ABC=90°,
∴∠C=90°﹣50°=40°,
∵AD⊥BC,△ADB与△ADB'关于直线AD对称,
∴∠AB′D=∠B=50°,
∵∠AB′D=∠C+∠CAB′,
∴∠CAB′=50°﹣40°=10°,
故答案为10°.
19.(3分)当x=2时,代数式÷(x﹣1)的值为 .
解:÷(x﹣1)
=
=,
当x=2时,原式==,
故答案为:.
20.(3分)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则DF的长为 1 .
解:∵DG=GE,
∴S△ADG=S△AEG=2,
∴S△ADE=4,
由翻折可知,△ADB≌△ADE,BE⊥AD,
∴S△ABD=S△ADE=4,∠BFD=90°,
∴?(AF+DF)?BF=4,
∴?(3+DF)?2=4,
∴DF=1.
故答案为:1.
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
解:(1)原式=8x3?(﹣5xy2)
=﹣8x3?5xy2
=﹣40x4y2;
(2)原式=3x2+6x+2x+4
=3x2+8x+4.
22.(8分)计算:
(1);
(2).
【解答】(1)==0
(2)
=
=
=
23.(8分)解方程:
(1)(x﹣3)(x﹣2)+18=(x+9)(x+1);
(2)+1=.
解:(1)(x﹣3)(x﹣2)+18=(x+9)(x+1),
x2﹣5x+6+18=x2+10x+9,
﹣15x=﹣15,
x=1.
(2)方程两边同乘以(x﹣2),得x﹣3+x﹣2=﹣3,
移项及合并同类项,得2x=2,
系数化为1,得x=1,
检验:当x=1时,x﹣2≠0,
∴原分式方程的解是x=1.
24.(8分)如图,△ABD,△AEC都是等边三角形,连接BE,DC,BE交DC于点F.
(1)求证:BE=DC;
(2)求∠BFC的度数.
【解答】证明:(1)∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)令AB与DC的交点为G,
∵△BAE≌△DAC,
∴∠ABE=∠ADC,
∵∠BGD=∠ABE+∠BFG,∠BGD=∠ADC+∠DAG,
∴∠ABE+∠BFG=∠ADC+∠DAG,
∴∠BFG=∠DAG=60°,
∴∠BFC=180°﹣∠BFG=120°.
25.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.
如,第一次按键后,A,B两区分别显示:
(1)从初始状态按2次后,分别求A,B两区显示的结果;
(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.
解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;
(2)这个和不能为负数,
理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;
∵(2a﹣3)2≥0,
∴这个和不能为负数.
26.(10分)某商店想购进A、B两种商品,已知每件B种商品的进价比每件A种商品的进价多5元,且用300元购进A种商品的数量是用100元购进B种商品数量的4倍.
(1)求每件A种商品和每件B种商品的进价分别是多少元?
(2)商店决定购进A、B两种商品共50件,A种商品加价5元出售,B种商品比进价提高20%后出售,要使所有商品全部出售后利润不少于210元,求A种商品至少购进多少件?
解:(1)设每件A商品的进价为x元,则每件B商品的进价为(x+5)元,
由题意得:=×4,
解得:x=15,
经检验,x=15是原分式方程的解,且符合题意,
则x+5=20,
答:每件A商品的进价为15元,每件B商品的进价为20元;
(2)设购进A商品a件,
由题意得:5a+20×20%(50﹣a)≥210,
解得:a≥10,
答:A种商品至少购进10件.
27.(10分)已知:在△ABC中,AB=AC,点D在BA的延长线上,DE∥AC交BC的延长线于点E.
(1)如图1,求证:DB=DE;
(2)如图2,作△DBE的高EF,连接AE,若∠DEA=∠FEA,求证:∠AEB=45°;
(3)如图3,在(2)的条件下,过点B作BG⊥AE于点G,BG交AC于点H,若CE=4,且四边形CEGH的面积是24,求BH的长.
【解答】证明:(1)∵AB=AC,
∴∠B=∠ACB,
∵DE∥AC,
∴∠ACB=∠E,
∴∠B=∠E,
∴DB=DE;
(2)令∠DEA=α,则∠FEA=α,∠FED=2α,
∵EF是△DBE的高,
∴EF⊥DB,
∴∠DFE=90°,
∴∠D=90°﹣∠DEF=90°﹣2α,
∵∠B+∠DEB+∠D=180°,
∴2∠DEB+90°﹣2α=180°,
∴∠DEB=45°+α,
∴∠AEB=∠DEB﹣∠DEA=45°+α﹣α=45°,
(3)如图3,过点C作CR⊥AE于R,过点R作RT⊥CE于T,
则∠CRE=∠CTR=∠ETR=90°,
∵∠AEB=45°,
∴∠RCE=∠ERT=45°=∠CRT,
∴RC=RE,ET=RT=CT=,
∵,
∴,
∴ER=CR=4,
∵DE∥AC,
∴∠CAR=∠DEA=α,
∵BG⊥AE,
∴∠BGE=90°,
∴∠GBE=90°﹣∠AEB=45°,
∴∠ABG=∠ABC﹣∠GBE=∠DEB﹣∠GBE=45°+α﹣45°=α=∠CAR,
∵∠AGB=∠CRA=90°,
∴△ABG≌△CAR(AAS),
∴S△ABG=S△CAR,AG=CR=4,
∴S△ABG﹣S△AGH=S△CAR﹣S△AGH,
∴S△ABH=S四边形CRGH,
∵S四边形CEGH=S四边形CRGH+S△CER,
∴,
∴S△ABH=S四边形CRGH=16,
∴,
∴,
∴BH=8.
一、选择题(共10小题).
1.(3分)下列方程中,是分式方程的是( )
A.+=1 B.x+=2 C.2x=x﹣5 D.x﹣4y=1
2.(3分)下列图案中不是轴对称图形的是( )
A. B.
C. D.
3.(3分)下列运算中,正确的是( )
A.a2?a3=a5 B.(a2)3=a5 C.a6÷a2=a3 D.a6﹣a2=a4
4.(3分)若分式的值为0,则x的值是( )
A.1或﹣1 B.1 C.﹣1 D.0
5.(3分)计算3a(5a﹣2b)的结果是( )
A.15a﹣6ab B.8a2﹣6ab C.15a2﹣5ab D.15a2﹣6ab
6.(3分)下列计算正确的是( )
A.﹣= B.= C.= D.﹣=6
7.(3分)计算(﹣3)0﹣2﹣3的结果是( )
A.﹣ B. C.6 D.7
8.(3分)若a≠b,则下列分式化简正确的是( )
A. B. C.= D.=
9.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
10.(3分)若的整数部分为x,小数部分为y,则x﹣y的值是( )
A.1 B. C.3﹣3 D.3
二、填空题(共10小题).
11.(3分)0.0012用科学记数法表示为 .
12.(3分)若分式有意义,则字母x满足的条件是 .
13.(3分)把多项式a3b﹣ab分解因式的结果为 .
14.(3分)计算﹣的结果是 .
15.(3分)计算:28x4y2÷7x3y= .
16.(3分)一个长方形的长和面积分别是和4,则这个长方形的宽为 .
17.(3分)等腰三角形的一个角是80°,则它的底角是 .
18.(3分)如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 .
19.(3分)当x=2时,代数式÷(x﹣1)的值为 .
20.(3分)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则DF的长为 .
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
22.(8分)计算:
(1);
(2).
23.(8分)解方程:
(1)(x﹣3)(x﹣2)+18=(x+9)(x+1);
(2)+1=.
24.(8分)如图,△ABD,△AEC都是等边三角形,连接BE,DC,BE交DC于点F.
(1)求证:BE=DC;
(2)求∠BFC的度数.
25.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.
如,第一次按键后,A,B两区分别显示:
(1)从初始状态按2次后,分别求A,B两区显示的结果;
(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.
26.(10分)某商店想购进A、B两种商品,已知每件B种商品的进价比每件A种商品的进价多5元,且用300元购进A种商品的数量是用100元购进B种商品数量的4倍.
(1)求每件A种商品和每件B种商品的进价分别是多少元?
(2)商店决定购进A、B两种商品共50件,A种商品加价5元出售,B种商品比进价提高20%后出售,要使所有商品全部出售后利润不少于210元,求A种商品至少购进多少件?
27.(10分)已知:在△ABC中,AB=AC,点D在BA的延长线上,DE∥AC交BC的延长线于点E.
(1)如图1,求证:DB=DE;
(2)如图2,作△DBE的高EF,连接AE,若∠DEA=∠FEA,求证:∠AEB=45°;
(3)如图3,在(2)的条件下,过点B作BG⊥AE于点G,BG交AC于点H,若CE=4,且四边形CEGH的面积是24,求BH的长.
参考答案
一、选择题(每小题3分,共计30分)
1.(3分)下列方程中,是分式方程的是( )
A.+=1 B.x+=2 C.2x=x﹣5 D.x﹣4y=1
解:A、该方程是一元一次方程,故本选项不符合题意;
B、该方程符合分式方程的定义,故本选项符合题意;
C、该方程是一元一次方程,故本选项不符合题意;
D、该方程是二元一次方程,故本选项不符合题意;
故选:B.
2.(3分)下列图案中不是轴对称图形的是( )
A. B.
C. D.
解:A、是轴对称图形,故本选项不合题意;
B、是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项符合题意;
D、是轴对称图形,故本选项不合题意;
故选:C.
3.(3分)下列运算中,正确的是( )
A.a2?a3=a5 B.(a2)3=a5 C.a6÷a2=a3 D.a6﹣a2=a4
解:A、a2?a3=a2+3=a5,本选项正确;
B、(a2)3=a6,本选项错误;
C、a6÷a2=a6﹣2=a4,本选项错误;
D、a6与﹣a2不是同类项,不能合并,本选项错误;
故选:A.
4.(3分)若分式的值为0,则x的值是( )
A.1或﹣1 B.1 C.﹣1 D.0
解:根据题意知,x﹣1=0,
解得x=1.
故选:B.
5.(3分)计算3a(5a﹣2b)的结果是( )
A.15a﹣6ab B.8a2﹣6ab C.15a2﹣5ab D.15a2﹣6ab
解:3a(5a﹣2b)=15a2﹣6ab.
故选:D.
6.(3分)下列计算正确的是( )
A.﹣= B.= C.= D.﹣=6
解:A、原式=2﹣,所以A选项错误;
B、原式=2+3=5,所以B选项错误;
C、原式=,所以C选项正确;
D、原式=5﹣=4,所以D选项错误.
故选:C.
7.(3分)计算(﹣3)0﹣2﹣3的结果是( )
A.﹣ B. C.6 D.7
解:原式=1﹣
=.
故选:B.
8.(3分)若a≠b,则下列分式化简正确的是( )
A. B. C.= D.=
解:∵a≠b,
∴,故选项A错误;
,故选项B错误;
≠,故选项C错误;
=,故选项D正确;
故选:D.
9.(3分)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
解:由作图知,MN是线段BC的垂直平分线,
∴BD=CD,
∵AC=6,AD=2,
∴BD=CD=4,
故选:C.
10.(3分)若的整数部分为x,小数部分为y,则x﹣y的值是( )
A.1 B. C.3﹣3 D.3
解:∵1,
∴x=1,y=﹣1,
∴x﹣y=×1﹣(﹣1)=1,
故选:A.
二、填空题(每小题3分,共计30分)
11.(3分)0.0012用科学记数法表示为 1.2×10﹣3 .
解:将0.0012用科学记数法表示为1.2×10﹣3,
故答案是:1.2×10﹣3.
12.(3分)若分式有意义,则字母x满足的条件是 x≠0 .
解:由题意得:3x≠0,
解得x≠0.
故答案为:x≠0.
13.(3分)把多项式a3b﹣ab分解因式的结果为 ab(a+1)(a﹣l) .
解:a3b﹣ab
=ab(a2﹣1)
=ab(a+1)(a﹣1).
故答案为ab(a+1)(a﹣1).
14.(3分)计算﹣的结果是 .
解:原式=4﹣3
=,
故答案为:.
15.(3分)计算:28x4y2÷7x3y= 4xy .
解:28x4y2÷7x3y=4xy,
故答案为:4xy.
16.(3分)一个长方形的长和面积分别是和4,则这个长方形的宽为 2 .
解:由题意知:长方形的宽为:===2,
故答案为:2.
17.(3分)等腰三角形的一个角是80°,则它的底角是 50°或80° .
解:由题意知,分两种情况:
(1)当这个80°的角为顶角时,则底角=(180°﹣80°)÷2=50°;
(2)当这个80°的角为底角时,则另一底角也为80°.
故答案为:50°或80°.
18.(3分)如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 10° .
解:∵∠B=50°,∠ABC=90°,
∴∠C=90°﹣50°=40°,
∵AD⊥BC,△ADB与△ADB'关于直线AD对称,
∴∠AB′D=∠B=50°,
∵∠AB′D=∠C+∠CAB′,
∴∠CAB′=50°﹣40°=10°,
故答案为10°.
19.(3分)当x=2时,代数式÷(x﹣1)的值为 .
解:÷(x﹣1)
=
=,
当x=2时,原式==,
故答案为:.
20.(3分)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则DF的长为 1 .
解:∵DG=GE,
∴S△ADG=S△AEG=2,
∴S△ADE=4,
由翻折可知,△ADB≌△ADE,BE⊥AD,
∴S△ABD=S△ADE=4,∠BFD=90°,
∴?(AF+DF)?BF=4,
∴?(3+DF)?2=4,
∴DF=1.
故答案为:1.
三、解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.(8分)(1)(2x)3(﹣5xy2);
(2)(3x+2)(x+2).
解:(1)原式=8x3?(﹣5xy2)
=﹣8x3?5xy2
=﹣40x4y2;
(2)原式=3x2+6x+2x+4
=3x2+8x+4.
22.(8分)计算:
(1);
(2).
【解答】(1)==0
(2)
=
=
=
23.(8分)解方程:
(1)(x﹣3)(x﹣2)+18=(x+9)(x+1);
(2)+1=.
解:(1)(x﹣3)(x﹣2)+18=(x+9)(x+1),
x2﹣5x+6+18=x2+10x+9,
﹣15x=﹣15,
x=1.
(2)方程两边同乘以(x﹣2),得x﹣3+x﹣2=﹣3,
移项及合并同类项,得2x=2,
系数化为1,得x=1,
检验:当x=1时,x﹣2≠0,
∴原分式方程的解是x=1.
24.(8分)如图,△ABD,△AEC都是等边三角形,连接BE,DC,BE交DC于点F.
(1)求证:BE=DC;
(2)求∠BFC的度数.
【解答】证明:(1)∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)令AB与DC的交点为G,
∵△BAE≌△DAC,
∴∠ABE=∠ADC,
∵∠BGD=∠ABE+∠BFG,∠BGD=∠ADC+∠DAG,
∴∠ABE+∠BFG=∠ADC+∠DAG,
∴∠BFG=∠DAG=60°,
∴∠BFC=180°﹣∠BFG=120°.
25.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.
如,第一次按键后,A,B两区分别显示:
(1)从初始状态按2次后,分别求A,B两区显示的结果;
(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.
解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;
(2)这个和不能为负数,
理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;
∵(2a﹣3)2≥0,
∴这个和不能为负数.
26.(10分)某商店想购进A、B两种商品,已知每件B种商品的进价比每件A种商品的进价多5元,且用300元购进A种商品的数量是用100元购进B种商品数量的4倍.
(1)求每件A种商品和每件B种商品的进价分别是多少元?
(2)商店决定购进A、B两种商品共50件,A种商品加价5元出售,B种商品比进价提高20%后出售,要使所有商品全部出售后利润不少于210元,求A种商品至少购进多少件?
解:(1)设每件A商品的进价为x元,则每件B商品的进价为(x+5)元,
由题意得:=×4,
解得:x=15,
经检验,x=15是原分式方程的解,且符合题意,
则x+5=20,
答:每件A商品的进价为15元,每件B商品的进价为20元;
(2)设购进A商品a件,
由题意得:5a+20×20%(50﹣a)≥210,
解得:a≥10,
答:A种商品至少购进10件.
27.(10分)已知:在△ABC中,AB=AC,点D在BA的延长线上,DE∥AC交BC的延长线于点E.
(1)如图1,求证:DB=DE;
(2)如图2,作△DBE的高EF,连接AE,若∠DEA=∠FEA,求证:∠AEB=45°;
(3)如图3,在(2)的条件下,过点B作BG⊥AE于点G,BG交AC于点H,若CE=4,且四边形CEGH的面积是24,求BH的长.
【解答】证明:(1)∵AB=AC,
∴∠B=∠ACB,
∵DE∥AC,
∴∠ACB=∠E,
∴∠B=∠E,
∴DB=DE;
(2)令∠DEA=α,则∠FEA=α,∠FED=2α,
∵EF是△DBE的高,
∴EF⊥DB,
∴∠DFE=90°,
∴∠D=90°﹣∠DEF=90°﹣2α,
∵∠B+∠DEB+∠D=180°,
∴2∠DEB+90°﹣2α=180°,
∴∠DEB=45°+α,
∴∠AEB=∠DEB﹣∠DEA=45°+α﹣α=45°,
(3)如图3,过点C作CR⊥AE于R,过点R作RT⊥CE于T,
则∠CRE=∠CTR=∠ETR=90°,
∵∠AEB=45°,
∴∠RCE=∠ERT=45°=∠CRT,
∴RC=RE,ET=RT=CT=,
∵,
∴,
∴ER=CR=4,
∵DE∥AC,
∴∠CAR=∠DEA=α,
∵BG⊥AE,
∴∠BGE=90°,
∴∠GBE=90°﹣∠AEB=45°,
∴∠ABG=∠ABC﹣∠GBE=∠DEB﹣∠GBE=45°+α﹣45°=α=∠CAR,
∵∠AGB=∠CRA=90°,
∴△ABG≌△CAR(AAS),
∴S△ABG=S△CAR,AG=CR=4,
∴S△ABG﹣S△AGH=S△CAR﹣S△AGH,
∴S△ABH=S四边形CRGH,
∵S四边形CEGH=S四边形CRGH+S△CER,
∴,
∴S△ABH=S四边形CRGH=16,
∴,
∴,
∴BH=8.
同课章节目录
