2020-2021学年江苏省泰州市高三上学期期中数学试卷 (Word解析版)
文档属性
| 名称 | 2020-2021学年江苏省泰州市高三上学期期中数学试卷 (Word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览




文档简介
2020-2021学年江苏省泰州市高三(上)期中数学试卷
一、选择题(共8小题).
1.(5分)设集合M={x|log2x<1},集合N={x|﹣2<x<1}.则M∩N=( )
A.(0,1) B.(﹣2,2) C.(0,2) D.(﹣2,1)
2.(5分)设a,b∈R,i是虚数单位,则“ab=0”是“复数为纯虚数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.(5分)欧拉是瑞士著名数学家,他首先发现:eiθ=cosθ+isinθ(e为自然对数的底数,i为虚数单位),此结论被称为“欧拉公式”,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系.根据欧拉公式可知,eiπ=( )
A.1 B.0 C.﹣1 D.1+i
4.(5分)埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长除以其两倍的高度,得到的商为3.14159,这就是圆周率较为精确的近似值,金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米,因年久风化,顶端剥落10米,则胡夫金字塔现在的高度大约为( )
A.128.4米 B.132.4米 C.136.4米 D.110.4米
5.(5分)在平行四边形ABCD中,点E,F分别满足,.若,则实数λ+μ的值为( )
A. B. C. D.
6.(5分)函数f(x)=的图象大致为( )
A.
B.
C.
D.
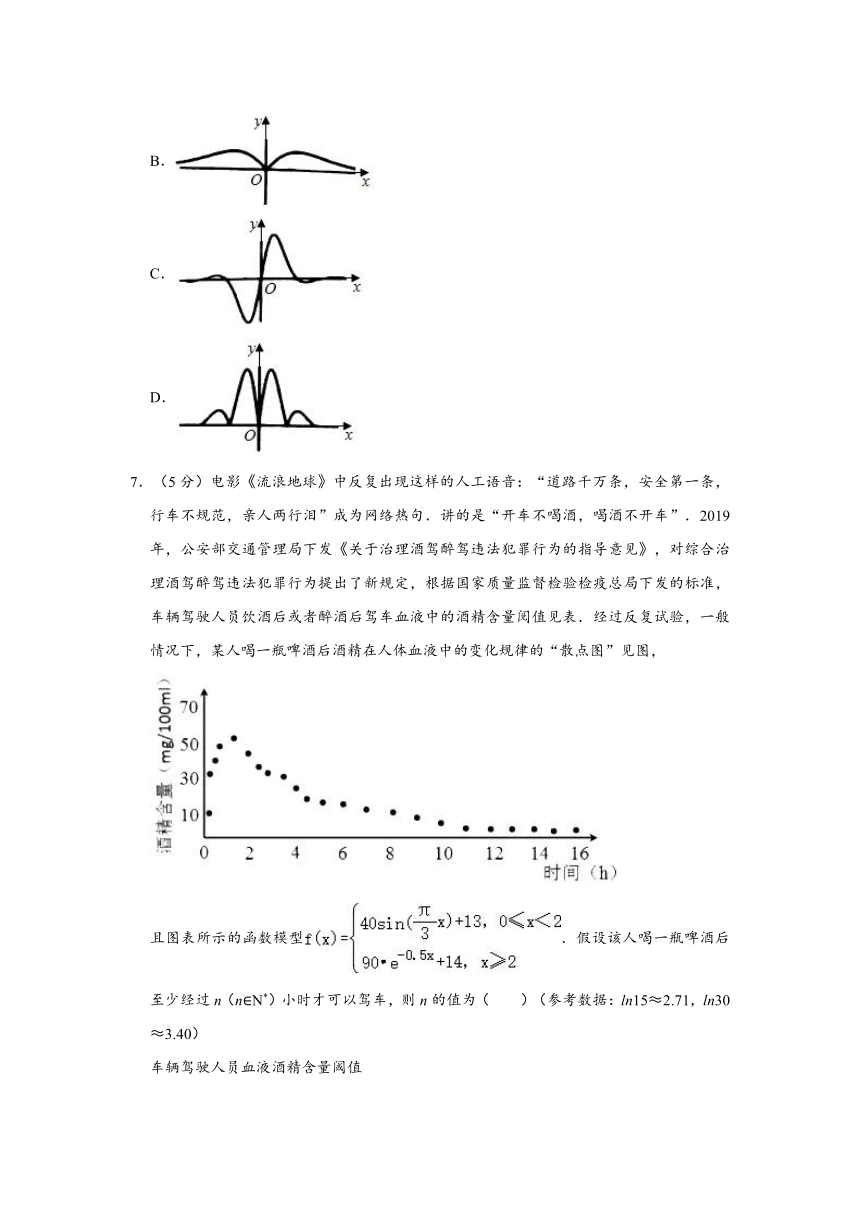
7.(5分)电影《流浪地球》中反复出现这样的人工语音:“道路千万条,安全第一条,行车不规范,亲人两行泪”成为网络热句.讲的是“开车不喝酒,喝酒不开车”.2019年,公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阅值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
且图表所示的函数模型.假设该人喝一瓶啤酒后至少经过n(n∈N*)小时才可以驾车,则n的值为( )(参考数据:ln15≈2.71,ln30≈3.40)
车辆驾驶人员血液酒精含量阈值
驾驶行为类别 阈值
(mg/100mL)
饮酒驾车 [20,80)
醉酒驾车 [80,+∞)
A.5 B.6 C.7 D.8
8.(5分)若实数a,b,c满足2a=log2b=log3c=k,其中k∈(1,2),则下列结论正确的是( )
A.ab>bc B.logab>logbc
C.a>logbc D.cb>ba
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.(5分)已知向量=(﹣3,2),=(﹣1,0),则下列选项正确的有( )
A.(+)?=4 B.(﹣3)⊥
C. D.
10.(5分)已知函数f(x)=ax3+bx2+cx(a<0)的导函数y=f'(x)的两个零点为1,2,则下列结论正确的有( )
A.abc<0
B.f(x)在区间[0,3]的最大值为0
C.f(x)只有一个零点
D.f(x)的极大值是正数
11.(5分)某港口一天24h内潮水的高度S(单位:m)随时间t(单位:h,0≤t≤24)的变化近似满足关系式S(t)=3sin(t+),则下列说法正确的有( )
A.S(t)在[0,2]上的平均变化率为m/h
B.相邻两次潮水高度最高的时间间距为24h
C.当t=6时,潮水的高度会达到一天中最低
D.18时潮水起落的速度为m/h
12.(5分)在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是棱BC的中点,点Q是底面A1B1C1D1上的动点,且AP⊥D1Q,则下列说法正确的有( )
A.DP与D1Q所成角的最大值为
B.四面体ABPQ的体积不变
C.△AA1Q的面积有最小值
D.平面D1PQ截正方体所得截面面积不变
三、填空题(共4小题).
13.(5分)已知,则cos2θ的值为 .
14.(5分)乒乓球被称为中国的“国球”,目前国际比赛用球的直径为4cm.某厂家计划生产乒乓球包装盒,包装盒为长方体,每盒装6个乒乓球,现有两种方案,方案甲:6个乒乓球放一排;方案乙:6个乒乓球并排放置两排,每排放3个,乒乓球与盒子、以及乒乓球之间紧密接触,确保用料最省,则方案甲中包装盒的表面积比方案乙中包装盒的表面积多 cm2.
15.(5分)已知正实数x,y满足x+y=1,则+的最小值为 .
16.(5分)已知直三棱柱ABC﹣A1B1C1中,AB=BC=1,AC=,侧棱AA1=2,则该三棱柱外接球的体积为 .
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(10分)设集合A=,B={x|x2﹣2mx+m2﹣4<0}.
(1)当m=2时,求A∩B;
(2)若A∪B=B,求实数m的取值范围.
18.(12分)已知向量=(cosx,﹣1),=(sinx,cos2x),函数.
(1)求函数f(x)的单调递增区间;
(2)求函数f(x)在区间[,0]上的最大值和最小值,并求出相应的x的值.
19.(12分)已知△ABC的内角A,B,C所对的边分别是a,b,c,A为锐角,在以下三个条件中任选一个:①(b﹣3c)cosA+acosB=0;②sin2+cos2A=;③;并解答以下问题:
(1)若选_____(填序号),求cosA的值;
(2)在(1)的条件下,若a=2,求△ABC面积S的最大值.
20.(12分)如图,在四棱锥P﹣ABCD中,PD=2,AB=3,AD=,∠DAB=90°,△BCD为正三角形,E是CD的中点,DE=PE,PD⊥BC.
(1)求证:平面PDE⊥平面PBC;
(2)求二面角P﹣BC﹣D的余弦值;
(3)求四棱锥P﹣ABCD的体积.
21.(12分)已知函数f(x)=2x,g(x)=f(x)+f(|x|).
(1)解不等式:f(2x)﹣f(x+1)>3;
(2)当x∈[﹣1,]时,求函数g(x)的值域;
(3)若?x1∈(0,+∞),?x2∈[﹣1,0],使得g(2x1)+ag(x1)+2g(x2)>0成立,求实数a的取值范围.
22.(12分)已知函数f(x)=x2﹣lnx,g(x)=kx.
(1)求函数f(x)的最小值;
(2)若g(x)是f(x)的切线,求实数k的值;
(3)若f(x)与g(x)的图象有两个不同交点A(x1,y1),B(x2,y2),求证:x1x2>1.
参考答案
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.(5分)设集合M={x|log2x<1},集合N={x|﹣2<x<1}.则M∩N=( )
A.(0,1) B.(﹣2,2) C.(0,2) D.(﹣2,1)
解:∵M={x|0<x<2},N={x|﹣2<x<1},
∴M∩N=(0,1).
故选:A.
2.(5分)设a,b∈R,i是虚数单位,则“ab=0”是“复数为纯虚数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:因为“ab=0”得a=0或b=0,只有a=0,并且b≠0,复数为纯虚数,否则不成立;
复数=a﹣bi为纯虚数,所以a=0并且b≠0,所以ab=0,
因此a,b∈R,i是虚数单位,则“ab=0”是“复数为纯虚数”的必要不充分条件.
故选:B.
3.(5分)欧拉是瑞士著名数学家,他首先发现:eiθ=cosθ+isinθ(e为自然对数的底数,i为虚数单位),此结论被称为“欧拉公式”,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系.根据欧拉公式可知,eiπ=( )
A.1 B.0 C.﹣1 D.1+i
解:根据eiθ=cosθ+isinθ,
可知eiπ==﹣1.
故选:C.
4.(5分)埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长除以其两倍的高度,得到的商为3.14159,这就是圆周率较为精确的近似值,金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米,因年久风化,顶端剥落10米,则胡夫金字塔现在的高度大约为( )
A.128.4米 B.132.4米 C.136.4米 D.110.4米
解:设金字塔风化前的形状如图,
∵|AB|=230,∴其底面周长为230×4=920,
由题意可得:=3.14159,
∴|PO|=146.42.
∴胡夫金字塔现高大约为146.42﹣10=136.42米.
结合选项可得,胡夫金字塔现高大约为136.4米.
故选:C.
5.(5分)在平行四边形ABCD中,点E,F分别满足,.若,则实数λ+μ的值为( )
A. B. C. D.
解:由题意可知,.,
,,
∴,
,
∴,又,
则,,
∴,
故选:B.
6.(5分)函数f(x)=的图象大致为( )
A.
B.
C.
D.
解:f(﹣x)==﹣f(x),
∴函数f(x)为奇函数,其图象关于原点对称,故排除BD,
令g(x)=sinx+x,x>0,
∴g′(x)=cosx+1≥0,
∴g(x)在(0,+∞)上单调递增,
∴g(x)>g(0)=0,
当x>0时,3x+3﹣x>0,
∴当x>0时,f(x)>0,故排除C,
故选:A.
7.(5分)电影《流浪地球》中反复出现这样的人工语音:“道路千万条,安全第一条,行车不规范,亲人两行泪”成为网络热句.讲的是“开车不喝酒,喝酒不开车”.2019年,公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阅值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
且图表所示的函数模型.假设该人喝一瓶啤酒后至少经过n(n∈N*)小时才可以驾车,则n的值为( )(参考数据:ln15≈2.71,ln30≈3.40)
车辆驾驶人员血液酒精含量阈值
驾驶行为类别 阈值
(mg/100mL)
饮酒驾车 [20,80)
醉酒驾车 [80,+∞)
A.5 B.6 C.7 D.8
解:由散点图可得该人喝一瓶啤酒后的2个小时内,其酒精含量阈值大于20,
令,得,
解得n>2ln15≈2×2.71=5.42,
∵n∈N*,∴n的值为6.
故选:B.
8.(5分)若实数a,b,c满足2a=log2b=log3c=k,其中k∈(1,2),则下列结论正确的是( )
A.ab>bc B.logab>logbc
C.a>logbc D.cb>ba
解:∵2a=log2b=log3c=k,∴a=log2k,b=2k,c=3k,
∵k∈(1,2),∴0<a<1,b>2,c>3,b<c,
∴ab<a0=1,bc>b0=1,∴ab<bc,即A错误;
logab<loga1=0,logbc>logb1=0,∴logab<logbc,即B错误;
0<a<1,3k>2k>1,c>b>1,logbc>logbb=1,∴a<logbc,即C错误;
cb>c>b,ba<b,∴cb>ba,即D正确.
故选:D.
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.(5分)已知向量=(﹣3,2),=(﹣1,0),则下列选项正确的有( )
A.(+)?=4 B.(﹣3)⊥
C. D.
解:由题意,可知
对于A:∵+=(﹣4,2),
∴(+)?=﹣4×(﹣1)+2×0=4,故选项A正确,
对于B:∵﹣3=(﹣3﹣3×(﹣1),2﹣3×0)=(0,2),
∴(﹣3)?=0×(﹣1)+2×0=0,
∴(﹣3)⊥,故选项B正确,
对于C:∵﹣=(﹣2,2),∴|﹣|==2,
||=?=,
∴|﹣|≠||,故选项C不正确,
对于D:∵2=||2=(﹣3)2+22=13,
2+4?=||2+4?=(﹣1)2+02+4×[(﹣3)×(﹣1)+2×0]=13,
∴2=2+4?,故选项D正确,
∴正确选项为ABD.
故选:ABD.
10.(5分)已知函数f(x)=ax3+bx2+cx(a<0)的导函数y=f'(x)的两个零点为1,2,则下列结论正确的有( )
A.abc<0
B.f(x)在区间[0,3]的最大值为0
C.f(x)只有一个零点
D.f(x)的极大值是正数
解:f(x)=ax3+bx2+cx(a<0),
f′(x)=3ax2+2bx+c,
由题意得:1,2是方程3ax2+2bx+c=0的根,
故b=﹣a>0,c=6a<0,故abc>0,故A错误;
故f(x)=ax3﹣ax2+6ax,
显然f(x)在(﹣∞,1)递减,在(1,2)递增,在(2,+∞)递减,
故f(x)在[0,1)递减,在(1,2)递增,在(2,3]递减,
而f(0)=0,f(1)=a<0,f(2)=2a<0,f(3)=a<0,
故f(x)在[0,3]的最大值是0,故正确;
函数f(x)的大致图象如图示:
,
故函数f(x)只有1个零点,故C正确,D错误;
故选:BC.
11.(5分)某港口一天24h内潮水的高度S(单位:m)随时间t(单位:h,0≤t≤24)的变化近似满足关系式S(t)=3sin(t+),则下列说法正确的有( )
A.S(t)在[0,2]上的平均变化率为m/h
B.相邻两次潮水高度最高的时间间距为24h
C.当t=6时,潮水的高度会达到一天中最低
D.18时潮水起落的速度为m/h
解:根据题意,依次分析选项:
对于A,S(t)在[0,2]上的平均变化率==﹣,A错误,
对于B,S(t)=3sin(t+),其最小正周期为=24,则相邻两次潮水高度最高的时间间距为24h,B正确,
对于C,当t=6时,S(6)=3sin(×6+)=﹣3,不是S(t)的最小值,C错误,
对于D,S(t)=3sin(t+),其导数S′(t)=3(t+)′cos(t+)=cos(t+),则有S′(18)=,D正确,
故选:BD.
12.(5分)在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是棱BC的中点,点Q是底面A1B1C1D1上的动点,且AP⊥D1Q,则下列说法正确的有( )
A.DP与D1Q所成角的最大值为
B.四面体ABPQ的体积不变
C.△AA1Q的面积有最小值
D.平面D1PQ截正方体所得截面面积不变
解:在正方体ABCD﹣A1B1C1D1中,DD1⊥平面ABCD,
所以DD1⊥AP,
因为AP⊥DQ,所以AP⊥平面DD1Q,
所以AP⊥D1Q,
因为P为BC中点,记A1B1中点为E,
所以Q位于直线D1E上.
A:记B1C1中点为H,连结EH,D1H,
易知D1H∥DP,
所以DP与D1Q所成角即为∠ED1H,
因为正方体棱长为1,
所以,
解得:cos∠,
所以DP与D1Q所成角为定值,为,
故A错误;
B:A,B,P三点为定点,
所以S△ABP为定值,
因为Q位于平面A1B1C1D1中,A,B,P在平面ABCD中,
所以点Q到平面ABP的距离为定值,
所以四面体ABPQ的体积不变,
故B正确;
C:在正方体中,AA1⊥平面A1B1C1D1,
所以AA1⊥QA1,
所以,
在Rt△D1A1E中,A1D1=2,A1E=1,
所以点A1到D1E的距离的最小值为,
所以△AA1Q的面积有最小值为,
故C正确;
D:当Q不与D1重合时,D1与Q连线即为D1E,
故平面D1PQ即为平面D1PE,
此时截面固定,面积为定值,
当Q与D1重合时,两点确定一条直线,
则截面确定,此时面积为定值,
故D正确.
故选:BCD.
三、填空题(本大题共4小题,每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.(5分)已知,则cos2θ的值为 ﹣ .
解:因为,
所以=,解得tanθ=2,
所以cos2θ====﹣.
故答案为:﹣.
14.(5分)乒乓球被称为中国的“国球”,目前国际比赛用球的直径为4cm.某厂家计划生产乒乓球包装盒,包装盒为长方体,每盒装6个乒乓球,现有两种方案,方案甲:6个乒乓球放一排;方案乙:6个乒乓球并排放置两排,每排放3个,乒乓球与盒子、以及乒乓球之间紧密接触,确保用料最省,则方案甲中包装盒的表面积比方案乙中包装盒的表面积多 64 cm2.
解:方案甲:6个乒乓球放一排,包装盒是长为4×6=24,宽和高为4的长方体,
它的表面积为
S甲=2×(4×4+4×24+4×24)=416(cm2);
方案乙:6个乒乓球并排放置两排,每排放3个,包装盒是长为4×3=12,宽为4×2=8,高为4的长方体,
它的表面积为
S乙=2×(4×8+4×12+12×8)=352(cm2);
且S甲﹣S乙=416﹣352=64(cm2);
所以方案甲中包装盒的表面积比方案乙中包装盒的表面积多64cm2.
故答案为:64.
15.(5分)已知正实数x,y满足x+y=1,则+的最小值为 4+2 .
解:∵正实数x,y满足x+y=1,
∴y=1﹣x,x∈(0,1),
∴+=+=﹣1++=﹣1+,
令t=3﹣x∈(2,3),
则+=﹣1+=﹣1+=﹣1+≥﹣1+=﹣1+5+2=4+2,
当且仅当t=时取“=“,
故答案为:4+2.
16.(5分)已知直三棱柱ABC﹣A1B1C1中,AB=BC=1,AC=,侧棱AA1=2,则该三棱柱外接球的体积为 π .
解:∵△ABC中,AB=BC=1,AC=,
∴cos∠ABC==﹣,
∴sin∠ABC=,
∴△ABC的外接圆的半径r=×=1.
直三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上,且AA1=2,
则球O的半径R==.
∴球O的体积=R3=π.
故答案为:π.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(10分)设集合A=,B={x|x2﹣2mx+m2﹣4<0}.
(1)当m=2时,求A∩B;
(2)若A∪B=B,求实数m的取值范围.
解:A={x|﹣1<x<2},B={x|m﹣2<x<m+2},
(1)m=2时,B={x|0<x<4},
∴A∩B=(0,2);
(2)∵A∪B=B,
∴A?B,
∴,解得0≤m≤1,
∴实数m的取值范围为[0,1].
18.(12分)已知向量=(cosx,﹣1),=(sinx,cos2x),函数.
(1)求函数f(x)的单调递增区间;
(2)求函数f(x)在区间[,0]上的最大值和最小值,并求出相应的x的值.
解:(1)由题意,可知
=sinxcosx﹣cos2x
=?2sinxcosx﹣
=sin2x﹣cos2x﹣
=sin(2x﹣)﹣,
则由﹣+2kπ≤2x﹣≤+2kπ,k∈Z,可得
﹣+kπ≤x≤+kπ,k∈Z,
∴函数f(x)的单调递增区间为:[﹣+kπ,+kπ],k∈Z.
(2)由题意,可知
当x∈[,0]时,2x﹣∈[﹣,﹣],
根据正弦函数的性质,可知
当2x﹣=﹣,即x=﹣时,函数f(x)取得最小值f(x)min=﹣1﹣=﹣,
当2x﹣=﹣,即x=﹣时,函数f(x)取得最大值f(x)max=﹣=0.
19.(12分)已知△ABC的内角A,B,C所对的边分别是a,b,c,A为锐角,在以下三个条件中任选一个:①(b﹣3c)cosA+acosB=0;②sin2+cos2A=;③;并解答以下问题:
(1)若选_____(填序号),求cosA的值;
(2)在(1)的条件下,若a=2,求△ABC面积S的最大值.
解:(1)若选:①(b﹣3c)cosA+acosB=0,
由正弦定理可得:(sinB﹣3sinC)cosA+sinAcosB=0,
即:sin(A+B)=3sinCcosA,
可得:sinC=3sinCcosA,
因为:C为三角形内角,sinC>0,
可得:cosA=.
若选:②sin2+cos2A=,
可得+2cos2A﹣1=﹣,
可得36cos2A+9cosA﹣7=0,
解得cosA=,或﹣(由于A为锐角,舍去),
故cosA=.
若选:③,
由正弦定理可得:sinAsinB=sinB+sinBcosA,
因为sinB≠0,
可得sinA=1+cosA,可得sin2A=,
所以cos2A+=1,整理可得:3cos2A+2cosA﹣1=0,
解得cosA=,或﹣1(由于A为锐角,舍去).
(2)由余弦定理a2=b2+c2﹣2bccosA,
把cosA=,a=2代入可得:4=b2+c2﹣bc≥bc,可得bc≤3,当且仅当b=c时等号成立,
又因为A为三角形内角,可得sinA>0,则sinA==,
则S=bcsinA=bc,即S的最大值为.
20.(12分)如图,在四棱锥P﹣ABCD中,PD=2,AB=3,AD=,∠DAB=90°,△BCD为正三角形,E是CD的中点,DE=PE,PD⊥BC.
(1)求证:平面PDE⊥平面PBC;
(2)求二面角P﹣BC﹣D的余弦值;
(3)求四棱锥P﹣ABCD的体积.
【解答】证明:(1)∵△BCD为正三角形,E是BC的中点,∴BC⊥DE,
又∵BC⊥PD,PD∩DE=D,PD?平面PDE,DE?平面PDE,
∴BC⊥平面PDE.
∵BC?平面PBC,∴平面PDE⊥平面PBC;
解:(2)由(1)知,BC⊥平面PDE,又PE?平面PDE,
故PE⊥BC,又DE⊥BC,故∠PED为二面角P﹣BC﹣D的平面角,
△ABD中,AB=3,AD=,∠DAB=90°,
故BD=.
又△BCD为正三角形,故DE=,
又PE=DE,则PE=3,又PD=2,
故△PDE中,由余弦定理得:cos∠PED=,
因此,二面角P﹣BC﹣D的余弦值为;
解:(3)由(2)知,sin∠PED=,
作PH⊥DE于H,则PH=PE?sin∠PED=,
由(1)知,BC⊥平面PDE,又PH?平面PDE,
故PH⊥BC,又PH⊥DE,BC∩DE=E,BC?平面ABCD,DE?平面ABCD,
∴PH⊥平面ABCD,
故=.
21.(12分)已知函数f(x)=2x,g(x)=f(x)+f(|x|).
(1)解不等式:f(2x)﹣f(x+1)>3;
(2)当x∈[﹣1,]时,求函数g(x)的值域;
(3)若?x1∈(0,+∞),?x2∈[﹣1,0],使得g(2x1)+ag(x1)+2g(x2)>0成立,求实数a的取值范围.
解:(1)∵f(x)=2x,f(2x)﹣f(x+1)>3,
∴22x﹣2x+1>3,∴(2x﹣3)(2x+1)>0,
∴2x>3,∴x>log23,
∴不等式的解集为{x|x>log23}.
(2),
当x∈[﹣1,0]时 ,
∴g(x)在[﹣1,0]上单调递减,又,∴;
当时,,
综上,当时,g(x)的值域为.
(3)当x1>0,x2∈[﹣1,0]时 ,
?x1>0,?x2∈[﹣1,0],使得g(2x1)+ag(x1)+2g(x2)>0成立,
即g(2x1)+ag(x1)+2g(x2)max>0,
由(2)知,,则g(2x1)+ag(x1)+5>0,
,
令,则?x>1,不等式恒成立,
∵,当且仅当,即时取等号,
∴,∴,
∴a的取值范围为.
22.(12分)已知函数f(x)=x2﹣lnx,g(x)=kx.
(1)求函数f(x)的最小值;
(2)若g(x)是f(x)的切线,求实数k的值;
(3)若f(x)与g(x)的图象有两个不同交点A(x1,y1),B(x2,y2),求证:x1x2>1.
解:(1)∵f(x)=x2﹣lnx,∴,
当时,f'(x)<0,∴f(x)在上单调递减;
当时,f'(x)>0,∴f(x)在上单调递增.
故函数f(x)的最小值为.
(2)若g(x)是f(x)的切线,设切点为(x0,f(x0)),
则过点(x0,f(x0))的切线方程为y=f'(x0)(x﹣x0)+f(x0),
即,即,
由题意知,
令h(x)=﹣x2+1﹣lnx(x>0),则x>0时,,
∴h(x)=﹣x2+1﹣lnx在(0,+∞)上单调递增,又h(1)=0,
∴有唯一的实根x0=1,则.
(3)证明:由题意,知,
两式相加,得,
两式相减,得,即,
∴,即,
不妨令0<x1<x2,记,则=,
令,则,
∴在(1,+∞)上单调递增,则,
∴,因而lnx1x2+2x1x2=,
令G(x)=lnx+2x,则x>0时,,
∴G(x)在(0,+∞)上单调递增,
∵G(x1x2)=lnx1x2+2x1x2>2=G(1),
∴x1x2>1.
一、选择题(共8小题).
1.(5分)设集合M={x|log2x<1},集合N={x|﹣2<x<1}.则M∩N=( )
A.(0,1) B.(﹣2,2) C.(0,2) D.(﹣2,1)
2.(5分)设a,b∈R,i是虚数单位,则“ab=0”是“复数为纯虚数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.(5分)欧拉是瑞士著名数学家,他首先发现:eiθ=cosθ+isinθ(e为自然对数的底数,i为虚数单位),此结论被称为“欧拉公式”,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系.根据欧拉公式可知,eiπ=( )
A.1 B.0 C.﹣1 D.1+i
4.(5分)埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长除以其两倍的高度,得到的商为3.14159,这就是圆周率较为精确的近似值,金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米,因年久风化,顶端剥落10米,则胡夫金字塔现在的高度大约为( )
A.128.4米 B.132.4米 C.136.4米 D.110.4米
5.(5分)在平行四边形ABCD中,点E,F分别满足,.若,则实数λ+μ的值为( )
A. B. C. D.
6.(5分)函数f(x)=的图象大致为( )
A.
B.
C.
D.
7.(5分)电影《流浪地球》中反复出现这样的人工语音:“道路千万条,安全第一条,行车不规范,亲人两行泪”成为网络热句.讲的是“开车不喝酒,喝酒不开车”.2019年,公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阅值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
且图表所示的函数模型.假设该人喝一瓶啤酒后至少经过n(n∈N*)小时才可以驾车,则n的值为( )(参考数据:ln15≈2.71,ln30≈3.40)
车辆驾驶人员血液酒精含量阈值
驾驶行为类别 阈值
(mg/100mL)
饮酒驾车 [20,80)
醉酒驾车 [80,+∞)
A.5 B.6 C.7 D.8
8.(5分)若实数a,b,c满足2a=log2b=log3c=k,其中k∈(1,2),则下列结论正确的是( )
A.ab>bc B.logab>logbc
C.a>logbc D.cb>ba
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.(5分)已知向量=(﹣3,2),=(﹣1,0),则下列选项正确的有( )
A.(+)?=4 B.(﹣3)⊥
C. D.
10.(5分)已知函数f(x)=ax3+bx2+cx(a<0)的导函数y=f'(x)的两个零点为1,2,则下列结论正确的有( )
A.abc<0
B.f(x)在区间[0,3]的最大值为0
C.f(x)只有一个零点
D.f(x)的极大值是正数
11.(5分)某港口一天24h内潮水的高度S(单位:m)随时间t(单位:h,0≤t≤24)的变化近似满足关系式S(t)=3sin(t+),则下列说法正确的有( )
A.S(t)在[0,2]上的平均变化率为m/h
B.相邻两次潮水高度最高的时间间距为24h
C.当t=6时,潮水的高度会达到一天中最低
D.18时潮水起落的速度为m/h
12.(5分)在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是棱BC的中点,点Q是底面A1B1C1D1上的动点,且AP⊥D1Q,则下列说法正确的有( )
A.DP与D1Q所成角的最大值为
B.四面体ABPQ的体积不变
C.△AA1Q的面积有最小值
D.平面D1PQ截正方体所得截面面积不变
三、填空题(共4小题).
13.(5分)已知,则cos2θ的值为 .
14.(5分)乒乓球被称为中国的“国球”,目前国际比赛用球的直径为4cm.某厂家计划生产乒乓球包装盒,包装盒为长方体,每盒装6个乒乓球,现有两种方案,方案甲:6个乒乓球放一排;方案乙:6个乒乓球并排放置两排,每排放3个,乒乓球与盒子、以及乒乓球之间紧密接触,确保用料最省,则方案甲中包装盒的表面积比方案乙中包装盒的表面积多 cm2.
15.(5分)已知正实数x,y满足x+y=1,则+的最小值为 .
16.(5分)已知直三棱柱ABC﹣A1B1C1中,AB=BC=1,AC=,侧棱AA1=2,则该三棱柱外接球的体积为 .
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(10分)设集合A=,B={x|x2﹣2mx+m2﹣4<0}.
(1)当m=2时,求A∩B;
(2)若A∪B=B,求实数m的取值范围.
18.(12分)已知向量=(cosx,﹣1),=(sinx,cos2x),函数.
(1)求函数f(x)的单调递增区间;
(2)求函数f(x)在区间[,0]上的最大值和最小值,并求出相应的x的值.
19.(12分)已知△ABC的内角A,B,C所对的边分别是a,b,c,A为锐角,在以下三个条件中任选一个:①(b﹣3c)cosA+acosB=0;②sin2+cos2A=;③;并解答以下问题:
(1)若选_____(填序号),求cosA的值;
(2)在(1)的条件下,若a=2,求△ABC面积S的最大值.
20.(12分)如图,在四棱锥P﹣ABCD中,PD=2,AB=3,AD=,∠DAB=90°,△BCD为正三角形,E是CD的中点,DE=PE,PD⊥BC.
(1)求证:平面PDE⊥平面PBC;
(2)求二面角P﹣BC﹣D的余弦值;
(3)求四棱锥P﹣ABCD的体积.
21.(12分)已知函数f(x)=2x,g(x)=f(x)+f(|x|).
(1)解不等式:f(2x)﹣f(x+1)>3;
(2)当x∈[﹣1,]时,求函数g(x)的值域;
(3)若?x1∈(0,+∞),?x2∈[﹣1,0],使得g(2x1)+ag(x1)+2g(x2)>0成立,求实数a的取值范围.
22.(12分)已知函数f(x)=x2﹣lnx,g(x)=kx.
(1)求函数f(x)的最小值;
(2)若g(x)是f(x)的切线,求实数k的值;
(3)若f(x)与g(x)的图象有两个不同交点A(x1,y1),B(x2,y2),求证:x1x2>1.
参考答案
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.(5分)设集合M={x|log2x<1},集合N={x|﹣2<x<1}.则M∩N=( )
A.(0,1) B.(﹣2,2) C.(0,2) D.(﹣2,1)
解:∵M={x|0<x<2},N={x|﹣2<x<1},
∴M∩N=(0,1).
故选:A.
2.(5分)设a,b∈R,i是虚数单位,则“ab=0”是“复数为纯虚数”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:因为“ab=0”得a=0或b=0,只有a=0,并且b≠0,复数为纯虚数,否则不成立;
复数=a﹣bi为纯虚数,所以a=0并且b≠0,所以ab=0,
因此a,b∈R,i是虚数单位,则“ab=0”是“复数为纯虚数”的必要不充分条件.
故选:B.
3.(5分)欧拉是瑞士著名数学家,他首先发现:eiθ=cosθ+isinθ(e为自然对数的底数,i为虚数单位),此结论被称为“欧拉公式”,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系.根据欧拉公式可知,eiπ=( )
A.1 B.0 C.﹣1 D.1+i
解:根据eiθ=cosθ+isinθ,
可知eiπ==﹣1.
故选:C.
4.(5分)埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长除以其两倍的高度,得到的商为3.14159,这就是圆周率较为精确的近似值,金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米,因年久风化,顶端剥落10米,则胡夫金字塔现在的高度大约为( )
A.128.4米 B.132.4米 C.136.4米 D.110.4米
解:设金字塔风化前的形状如图,
∵|AB|=230,∴其底面周长为230×4=920,
由题意可得:=3.14159,
∴|PO|=146.42.
∴胡夫金字塔现高大约为146.42﹣10=136.42米.
结合选项可得,胡夫金字塔现高大约为136.4米.
故选:C.
5.(5分)在平行四边形ABCD中,点E,F分别满足,.若,则实数λ+μ的值为( )
A. B. C. D.
解:由题意可知,.,
,,
∴,
,
∴,又,
则,,
∴,
故选:B.
6.(5分)函数f(x)=的图象大致为( )
A.
B.
C.
D.
解:f(﹣x)==﹣f(x),
∴函数f(x)为奇函数,其图象关于原点对称,故排除BD,
令g(x)=sinx+x,x>0,
∴g′(x)=cosx+1≥0,
∴g(x)在(0,+∞)上单调递增,
∴g(x)>g(0)=0,
当x>0时,3x+3﹣x>0,
∴当x>0时,f(x)>0,故排除C,
故选:A.
7.(5分)电影《流浪地球》中反复出现这样的人工语音:“道路千万条,安全第一条,行车不规范,亲人两行泪”成为网络热句.讲的是“开车不喝酒,喝酒不开车”.2019年,公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阅值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
且图表所示的函数模型.假设该人喝一瓶啤酒后至少经过n(n∈N*)小时才可以驾车,则n的值为( )(参考数据:ln15≈2.71,ln30≈3.40)
车辆驾驶人员血液酒精含量阈值
驾驶行为类别 阈值
(mg/100mL)
饮酒驾车 [20,80)
醉酒驾车 [80,+∞)
A.5 B.6 C.7 D.8
解:由散点图可得该人喝一瓶啤酒后的2个小时内,其酒精含量阈值大于20,
令,得,
解得n>2ln15≈2×2.71=5.42,
∵n∈N*,∴n的值为6.
故选:B.
8.(5分)若实数a,b,c满足2a=log2b=log3c=k,其中k∈(1,2),则下列结论正确的是( )
A.ab>bc B.logab>logbc
C.a>logbc D.cb>ba
解:∵2a=log2b=log3c=k,∴a=log2k,b=2k,c=3k,
∵k∈(1,2),∴0<a<1,b>2,c>3,b<c,
∴ab<a0=1,bc>b0=1,∴ab<bc,即A错误;
logab<loga1=0,logbc>logb1=0,∴logab<logbc,即B错误;
0<a<1,3k>2k>1,c>b>1,logbc>logbb=1,∴a<logbc,即C错误;
cb>c>b,ba<b,∴cb>ba,即D正确.
故选:D.
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.(5分)已知向量=(﹣3,2),=(﹣1,0),则下列选项正确的有( )
A.(+)?=4 B.(﹣3)⊥
C. D.
解:由题意,可知
对于A:∵+=(﹣4,2),
∴(+)?=﹣4×(﹣1)+2×0=4,故选项A正确,
对于B:∵﹣3=(﹣3﹣3×(﹣1),2﹣3×0)=(0,2),
∴(﹣3)?=0×(﹣1)+2×0=0,
∴(﹣3)⊥,故选项B正确,
对于C:∵﹣=(﹣2,2),∴|﹣|==2,
||=?=,
∴|﹣|≠||,故选项C不正确,
对于D:∵2=||2=(﹣3)2+22=13,
2+4?=||2+4?=(﹣1)2+02+4×[(﹣3)×(﹣1)+2×0]=13,
∴2=2+4?,故选项D正确,
∴正确选项为ABD.
故选:ABD.
10.(5分)已知函数f(x)=ax3+bx2+cx(a<0)的导函数y=f'(x)的两个零点为1,2,则下列结论正确的有( )
A.abc<0
B.f(x)在区间[0,3]的最大值为0
C.f(x)只有一个零点
D.f(x)的极大值是正数
解:f(x)=ax3+bx2+cx(a<0),
f′(x)=3ax2+2bx+c,
由题意得:1,2是方程3ax2+2bx+c=0的根,
故b=﹣a>0,c=6a<0,故abc>0,故A错误;
故f(x)=ax3﹣ax2+6ax,
显然f(x)在(﹣∞,1)递减,在(1,2)递增,在(2,+∞)递减,
故f(x)在[0,1)递减,在(1,2)递增,在(2,3]递减,
而f(0)=0,f(1)=a<0,f(2)=2a<0,f(3)=a<0,
故f(x)在[0,3]的最大值是0,故正确;
函数f(x)的大致图象如图示:
,
故函数f(x)只有1个零点,故C正确,D错误;
故选:BC.
11.(5分)某港口一天24h内潮水的高度S(单位:m)随时间t(单位:h,0≤t≤24)的变化近似满足关系式S(t)=3sin(t+),则下列说法正确的有( )
A.S(t)在[0,2]上的平均变化率为m/h
B.相邻两次潮水高度最高的时间间距为24h
C.当t=6时,潮水的高度会达到一天中最低
D.18时潮水起落的速度为m/h
解:根据题意,依次分析选项:
对于A,S(t)在[0,2]上的平均变化率==﹣,A错误,
对于B,S(t)=3sin(t+),其最小正周期为=24,则相邻两次潮水高度最高的时间间距为24h,B正确,
对于C,当t=6时,S(6)=3sin(×6+)=﹣3,不是S(t)的最小值,C错误,
对于D,S(t)=3sin(t+),其导数S′(t)=3(t+)′cos(t+)=cos(t+),则有S′(18)=,D正确,
故选:BD.
12.(5分)在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是棱BC的中点,点Q是底面A1B1C1D1上的动点,且AP⊥D1Q,则下列说法正确的有( )
A.DP与D1Q所成角的最大值为
B.四面体ABPQ的体积不变
C.△AA1Q的面积有最小值
D.平面D1PQ截正方体所得截面面积不变
解:在正方体ABCD﹣A1B1C1D1中,DD1⊥平面ABCD,
所以DD1⊥AP,
因为AP⊥DQ,所以AP⊥平面DD1Q,
所以AP⊥D1Q,
因为P为BC中点,记A1B1中点为E,
所以Q位于直线D1E上.
A:记B1C1中点为H,连结EH,D1H,
易知D1H∥DP,
所以DP与D1Q所成角即为∠ED1H,
因为正方体棱长为1,
所以,
解得:cos∠,
所以DP与D1Q所成角为定值,为,
故A错误;
B:A,B,P三点为定点,
所以S△ABP为定值,
因为Q位于平面A1B1C1D1中,A,B,P在平面ABCD中,
所以点Q到平面ABP的距离为定值,
所以四面体ABPQ的体积不变,
故B正确;
C:在正方体中,AA1⊥平面A1B1C1D1,
所以AA1⊥QA1,
所以,
在Rt△D1A1E中,A1D1=2,A1E=1,
所以点A1到D1E的距离的最小值为,
所以△AA1Q的面积有最小值为,
故C正确;
D:当Q不与D1重合时,D1与Q连线即为D1E,
故平面D1PQ即为平面D1PE,
此时截面固定,面积为定值,
当Q与D1重合时,两点确定一条直线,
则截面确定,此时面积为定值,
故D正确.
故选:BCD.
三、填空题(本大题共4小题,每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.(5分)已知,则cos2θ的值为 ﹣ .
解:因为,
所以=,解得tanθ=2,
所以cos2θ====﹣.
故答案为:﹣.
14.(5分)乒乓球被称为中国的“国球”,目前国际比赛用球的直径为4cm.某厂家计划生产乒乓球包装盒,包装盒为长方体,每盒装6个乒乓球,现有两种方案,方案甲:6个乒乓球放一排;方案乙:6个乒乓球并排放置两排,每排放3个,乒乓球与盒子、以及乒乓球之间紧密接触,确保用料最省,则方案甲中包装盒的表面积比方案乙中包装盒的表面积多 64 cm2.
解:方案甲:6个乒乓球放一排,包装盒是长为4×6=24,宽和高为4的长方体,
它的表面积为
S甲=2×(4×4+4×24+4×24)=416(cm2);
方案乙:6个乒乓球并排放置两排,每排放3个,包装盒是长为4×3=12,宽为4×2=8,高为4的长方体,
它的表面积为
S乙=2×(4×8+4×12+12×8)=352(cm2);
且S甲﹣S乙=416﹣352=64(cm2);
所以方案甲中包装盒的表面积比方案乙中包装盒的表面积多64cm2.
故答案为:64.
15.(5分)已知正实数x,y满足x+y=1,则+的最小值为 4+2 .
解:∵正实数x,y满足x+y=1,
∴y=1﹣x,x∈(0,1),
∴+=+=﹣1++=﹣1+,
令t=3﹣x∈(2,3),
则+=﹣1+=﹣1+=﹣1+≥﹣1+=﹣1+5+2=4+2,
当且仅当t=时取“=“,
故答案为:4+2.
16.(5分)已知直三棱柱ABC﹣A1B1C1中,AB=BC=1,AC=,侧棱AA1=2,则该三棱柱外接球的体积为 π .
解:∵△ABC中,AB=BC=1,AC=,
∴cos∠ABC==﹣,
∴sin∠ABC=,
∴△ABC的外接圆的半径r=×=1.
直三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上,且AA1=2,
则球O的半径R==.
∴球O的体积=R3=π.
故答案为:π.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(10分)设集合A=,B={x|x2﹣2mx+m2﹣4<0}.
(1)当m=2时,求A∩B;
(2)若A∪B=B,求实数m的取值范围.
解:A={x|﹣1<x<2},B={x|m﹣2<x<m+2},
(1)m=2时,B={x|0<x<4},
∴A∩B=(0,2);
(2)∵A∪B=B,
∴A?B,
∴,解得0≤m≤1,
∴实数m的取值范围为[0,1].
18.(12分)已知向量=(cosx,﹣1),=(sinx,cos2x),函数.
(1)求函数f(x)的单调递增区间;
(2)求函数f(x)在区间[,0]上的最大值和最小值,并求出相应的x的值.
解:(1)由题意,可知
=sinxcosx﹣cos2x
=?2sinxcosx﹣
=sin2x﹣cos2x﹣
=sin(2x﹣)﹣,
则由﹣+2kπ≤2x﹣≤+2kπ,k∈Z,可得
﹣+kπ≤x≤+kπ,k∈Z,
∴函数f(x)的单调递增区间为:[﹣+kπ,+kπ],k∈Z.
(2)由题意,可知
当x∈[,0]时,2x﹣∈[﹣,﹣],
根据正弦函数的性质,可知
当2x﹣=﹣,即x=﹣时,函数f(x)取得最小值f(x)min=﹣1﹣=﹣,
当2x﹣=﹣,即x=﹣时,函数f(x)取得最大值f(x)max=﹣=0.
19.(12分)已知△ABC的内角A,B,C所对的边分别是a,b,c,A为锐角,在以下三个条件中任选一个:①(b﹣3c)cosA+acosB=0;②sin2+cos2A=;③;并解答以下问题:
(1)若选_____(填序号),求cosA的值;
(2)在(1)的条件下,若a=2,求△ABC面积S的最大值.
解:(1)若选:①(b﹣3c)cosA+acosB=0,
由正弦定理可得:(sinB﹣3sinC)cosA+sinAcosB=0,
即:sin(A+B)=3sinCcosA,
可得:sinC=3sinCcosA,
因为:C为三角形内角,sinC>0,
可得:cosA=.
若选:②sin2+cos2A=,
可得+2cos2A﹣1=﹣,
可得36cos2A+9cosA﹣7=0,
解得cosA=,或﹣(由于A为锐角,舍去),
故cosA=.
若选:③,
由正弦定理可得:sinAsinB=sinB+sinBcosA,
因为sinB≠0,
可得sinA=1+cosA,可得sin2A=,
所以cos2A+=1,整理可得:3cos2A+2cosA﹣1=0,
解得cosA=,或﹣1(由于A为锐角,舍去).
(2)由余弦定理a2=b2+c2﹣2bccosA,
把cosA=,a=2代入可得:4=b2+c2﹣bc≥bc,可得bc≤3,当且仅当b=c时等号成立,
又因为A为三角形内角,可得sinA>0,则sinA==,
则S=bcsinA=bc,即S的最大值为.
20.(12分)如图,在四棱锥P﹣ABCD中,PD=2,AB=3,AD=,∠DAB=90°,△BCD为正三角形,E是CD的中点,DE=PE,PD⊥BC.
(1)求证:平面PDE⊥平面PBC;
(2)求二面角P﹣BC﹣D的余弦值;
(3)求四棱锥P﹣ABCD的体积.
【解答】证明:(1)∵△BCD为正三角形,E是BC的中点,∴BC⊥DE,
又∵BC⊥PD,PD∩DE=D,PD?平面PDE,DE?平面PDE,
∴BC⊥平面PDE.
∵BC?平面PBC,∴平面PDE⊥平面PBC;
解:(2)由(1)知,BC⊥平面PDE,又PE?平面PDE,
故PE⊥BC,又DE⊥BC,故∠PED为二面角P﹣BC﹣D的平面角,
△ABD中,AB=3,AD=,∠DAB=90°,
故BD=.
又△BCD为正三角形,故DE=,
又PE=DE,则PE=3,又PD=2,
故△PDE中,由余弦定理得:cos∠PED=,
因此,二面角P﹣BC﹣D的余弦值为;
解:(3)由(2)知,sin∠PED=,
作PH⊥DE于H,则PH=PE?sin∠PED=,
由(1)知,BC⊥平面PDE,又PH?平面PDE,
故PH⊥BC,又PH⊥DE,BC∩DE=E,BC?平面ABCD,DE?平面ABCD,
∴PH⊥平面ABCD,
故=.
21.(12分)已知函数f(x)=2x,g(x)=f(x)+f(|x|).
(1)解不等式:f(2x)﹣f(x+1)>3;
(2)当x∈[﹣1,]时,求函数g(x)的值域;
(3)若?x1∈(0,+∞),?x2∈[﹣1,0],使得g(2x1)+ag(x1)+2g(x2)>0成立,求实数a的取值范围.
解:(1)∵f(x)=2x,f(2x)﹣f(x+1)>3,
∴22x﹣2x+1>3,∴(2x﹣3)(2x+1)>0,
∴2x>3,∴x>log23,
∴不等式的解集为{x|x>log23}.
(2),
当x∈[﹣1,0]时 ,
∴g(x)在[﹣1,0]上单调递减,又,∴;
当时,,
综上,当时,g(x)的值域为.
(3)当x1>0,x2∈[﹣1,0]时 ,
?x1>0,?x2∈[﹣1,0],使得g(2x1)+ag(x1)+2g(x2)>0成立,
即g(2x1)+ag(x1)+2g(x2)max>0,
由(2)知,,则g(2x1)+ag(x1)+5>0,
,
令,则?x>1,不等式恒成立,
∵,当且仅当,即时取等号,
∴,∴,
∴a的取值范围为.
22.(12分)已知函数f(x)=x2﹣lnx,g(x)=kx.
(1)求函数f(x)的最小值;
(2)若g(x)是f(x)的切线,求实数k的值;
(3)若f(x)与g(x)的图象有两个不同交点A(x1,y1),B(x2,y2),求证:x1x2>1.
解:(1)∵f(x)=x2﹣lnx,∴,
当时,f'(x)<0,∴f(x)在上单调递减;
当时,f'(x)>0,∴f(x)在上单调递增.
故函数f(x)的最小值为.
(2)若g(x)是f(x)的切线,设切点为(x0,f(x0)),
则过点(x0,f(x0))的切线方程为y=f'(x0)(x﹣x0)+f(x0),
即,即,
由题意知,
令h(x)=﹣x2+1﹣lnx(x>0),则x>0时,,
∴h(x)=﹣x2+1﹣lnx在(0,+∞)上单调递增,又h(1)=0,
∴有唯一的实根x0=1,则.
(3)证明:由题意,知,
两式相加,得,
两式相减,得,即,
∴,即,
不妨令0<x1<x2,记,则=,
令,则,
∴在(1,+∞)上单调递增,则,
∴,因而lnx1x2+2x1x2=,
令G(x)=lnx+2x,则x>0时,,
∴G(x)在(0,+∞)上单调递增,
∵G(x1x2)=lnx1x2+2x1x2>2=G(1),
∴x1x2>1.
同课章节目录
