人教版数学七年级上册: 4.3.1 角 课件(共38张ppt)
文档属性
| 名称 | 人教版数学七年级上册: 4.3.1 角 课件(共38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 30.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 12:47:33 | ||
图片预览






文档简介
(共38张PPT)
4.3.1
角
人教版数学七年级上册
第四章
第三节
学习目标
能从静态和动态两个角度阐述角的定义;
能结合图形使用不同的方法表示角;
会进行度、分、秒的简单换算。
1
一、新知突破
2
二、典型例题
3
三、课堂练习
目
录
1
一、新知突破
观察左边的实物,你发现这些实物能抽象出什么样的几何图形?
——角
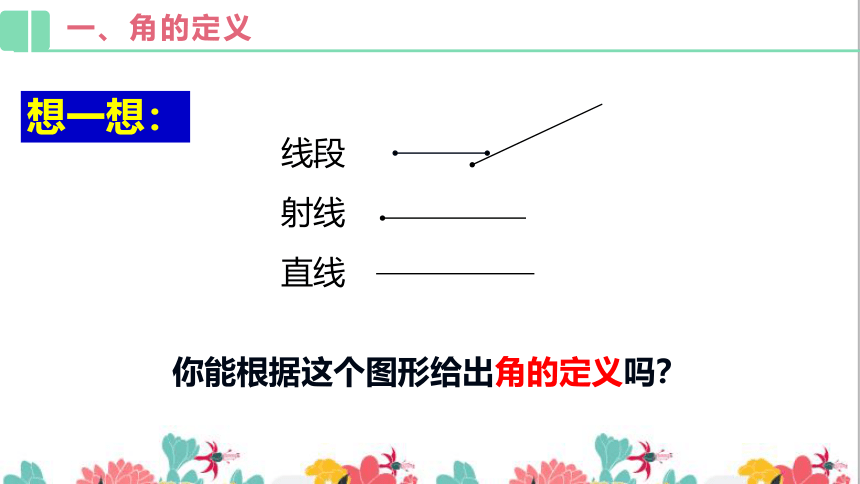
线段
射线
直线
你能根据这个图形给出角的定义吗?
想一想:
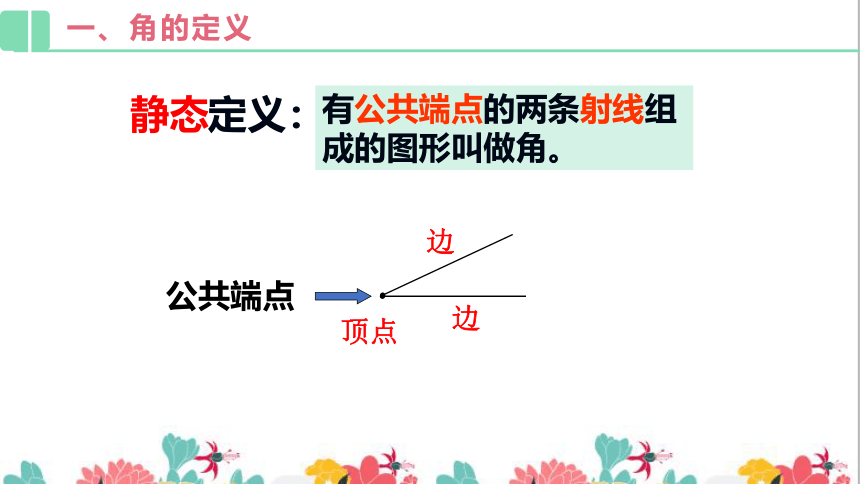
有公共端点的两条射线组成的图形叫做角。
定义:
静态
边
顶点
边
公共端点
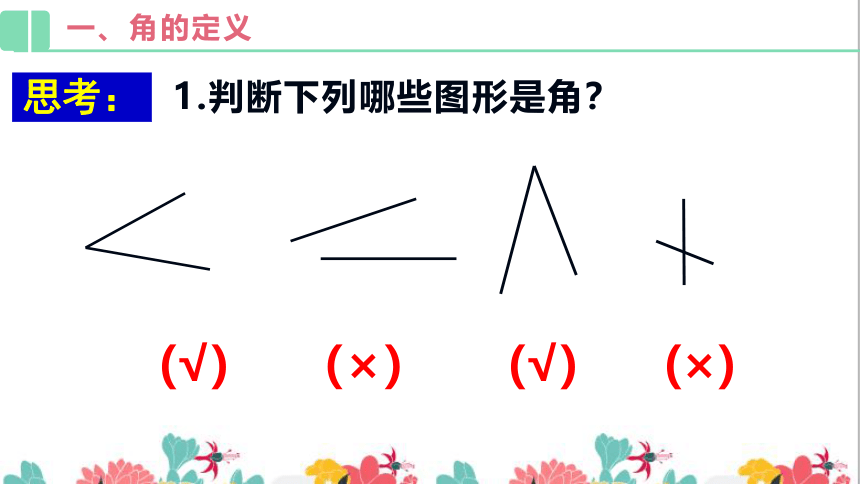
1.判断下列哪些图形是角?
(√)
(×)
(√)
(×)
思考:
2.下列说法是否正确,如果不正确,请说出错在哪里?
(×)
(×)
⑴
两条有公共端点的线段组成的图形叫角;
⑵
两条有公共点的射线组成的图形叫角。
思考:
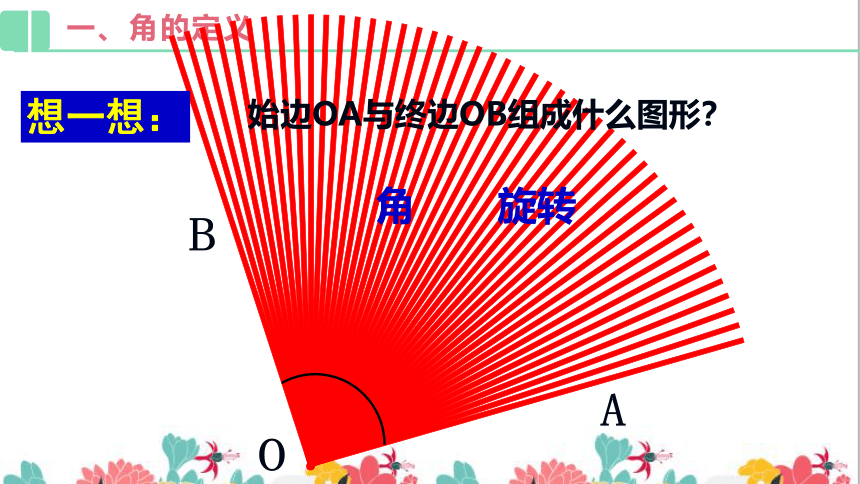
O
A
B
始边OA与终边OB组成什么图形?
角
旋转
想一想:
O
A
B
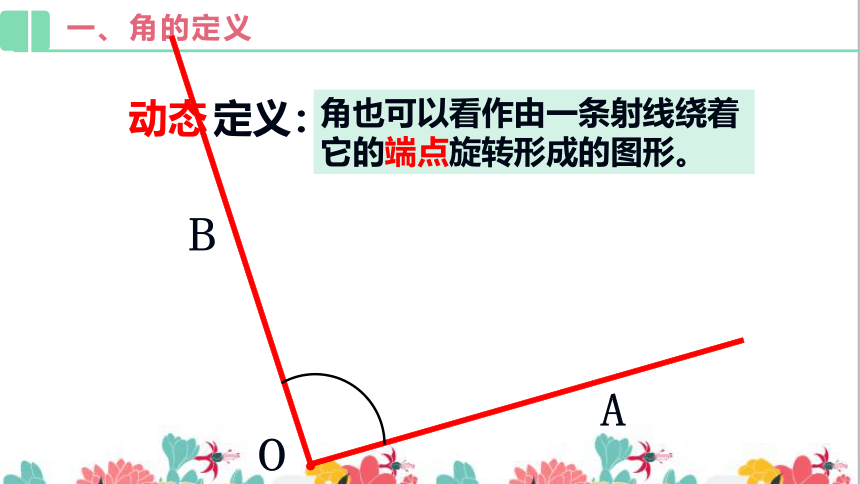
角也可以看作由一条射线绕着它的端点旋转形成的图形。
定义:
动态
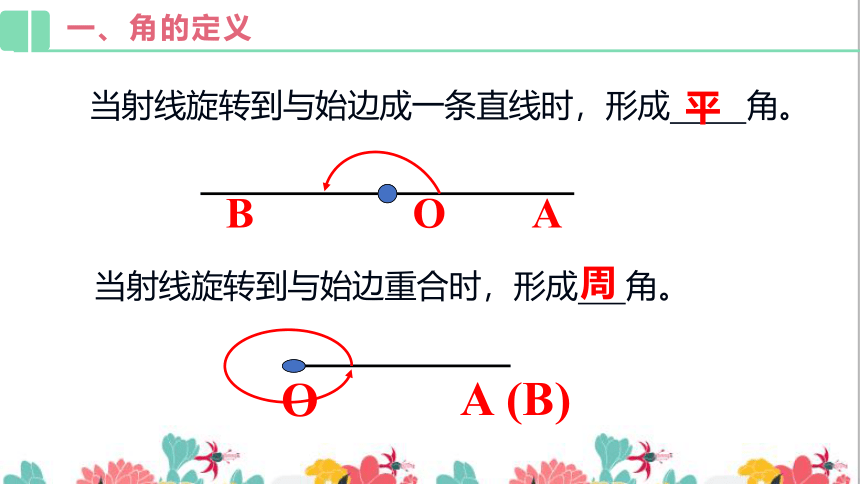
当射线旋转到与始边成一条直线时,形成
角。
当射线旋转到与始边重合时,形成
角。
平
周
O
A
B
O
A
(B)
角也可以看成是由一条射线绕着它的端点旋转而形成的图形。
有公共端点的两条射线所组成的图形叫做角。
定义:
O
A
B
·
A
O
B
第二个定义:
始边
终边
当始边OA与终边OB成一直线时形成了平角
180°
当始边OA与终边OB重合时形成了周角
360°
注意:无特别说明,我们
指的角是小于平角的角
静
动
归纳:
一共有哪些表示角的方法?
想一想:
∠α
O
A
B
①
①
用三个大写字母表示:
∠AOB
或
∠BOA
②
用顶点的大写字母表示:
③
用一个希腊字母表示:
④
用一个阿拉伯数字表示:
∠O
∠1
O
②
α
③
1
④
表示方法
注意事项
①用三个大写字母表示
表示顶点的字母要写在中间
②用顶点的大写字母表示
顶点处只有一个角
③用一个希腊字母表示
在靠近顶点的处画弧线,并写上希腊字母
④用一个阿拉伯数字表示
在靠近顶点的处画弧线,并写上数字
A
B
O
思考:
1.如图,还能把∠AOB
记作∠O
吗?为什么?
C
2.图中你还能找到哪些角,怎么表示呢?
∠AOC
和∠BOC
这是1°角
1°=60'
1''=
'
1′=60″
1'=
°
由此,我们可以得到度、分、秒是
进制的。
60
角的基本度量单位:
度、分、秒
分、秒的定义:
把
的角等分成60份,
①
②
把
的角等分成60份,
即:
角的度量工具:
量角器
类比
时间单位
每一份就是1分,记作
每一份就是1秒,记作
(60进制)
1周角
1平角
1直角
角的基本度量单位:
度、分、秒
1周角
=360°
=180°
=90
°
=2平角
=4直角
度
分秒
不足1度的化成分
不足1分的化成秒
分秒
度
秒
分
度
1°=60
′=3600
″
1.
度到分的换算
【例1】
1°=60'
1°是一个60′
2°是
个60′
两
即:2°=2×60′=120′
1′=60″
0.5′=
×
=
。
1′是一个
;
2′是
个
;
即:2′=2×
=
;
2.
分到秒的换算
两
60″
60″
60″
120″
30″
0.5
60″
【例2】
3.
分到度的换算
两
1′=
°
1′是一个
°
2′是
个
°
即:2′=2×
°=
°
【例3】
4.
秒到分的换算
2″是
个
′
两
1″=
′
1″是一个
′
即:2″=2×
′=
′
【例4】
2
二、典型例题
度分秒的互化
(1)
57.32°=
°
′
″;
解析:57.32?=57?+0.32×60′
=57?+19.2′
=57?19′+0.2×60″
=57?19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒.
(小数化整数)
57
19
12
【例1】
(2)
17°6′36″=
°.
17.11
解析:17°6′36″=17°+6′+
′′
=17°+6.6′
=17?+
°
=17.11?.
按1″=
′,1′=
°先把秒化成分,再把分化成度.
(整数化小数)
【例1】
300
18000
38
9
0.6
0.01
38.25
5°= ′=
″;38.15°= ° ′;36″= ′= °;
38°15′= °.
【例1】
如图,时钟显示为10:10时,时针与分针所夹
角度是
( )
A.90°
B.100°
C.105°
D.115°
解析:时针每小时旋转的夹角360°
÷12=30°,故10分钟,时针旋转的角度为5°,即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
【例2】
3
三、课堂练习
2.如图,其中小于180°的角共有(
)
1.教材P134 练习第1,2,3题.
练
习
C
A.3个
B.4个
C.5个
D.6个
3.若∠1=25°12′,∠2=25.12°,∠3=25.2°,则下列结论正确的是(
)
A.∠1=∠2
B.∠2=∠3
C.∠1=∠3
D.∠1=∠2=∠3
练
习
C
4.分别确定四个城市相应钟表上时针与分针所成的小于平角的角的度数,并填在相应的横线上.
巴黎时间
北京时间
伦敦时间
东京时间
30°
120°
0°
90°
练
习
练
习
5.如图,一共有多少个小于平角东京时间的角?按图中字母把它们表示出来,并指出哪些角可以用一个字母表示.
解:图中一共有14个小于平角的角,用字母表示为:∠ABF,∠FBD,∠ABD,∠ACB,∠ACF,∠FCD,∠BCF,∠ACD,∠AEB,∠BEC,∠CEF,∠AEF,∠A,∠F,其中∠A和∠F可用一个字母表示.
角的定义
有公共端点的两条射线组成的图形
一条射线绕着它的端点旋转而形成的图形
角的表示方法
用三个大写字母或一个大写字母表示
用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量
度、分、秒
1°=60′,1′=60″
谢
谢
!
4.3.1
角
人教版数学七年级上册
第四章
第三节
学习目标
能从静态和动态两个角度阐述角的定义;
能结合图形使用不同的方法表示角;
会进行度、分、秒的简单换算。
1
一、新知突破
2
二、典型例题
3
三、课堂练习
目
录
1
一、新知突破
观察左边的实物,你发现这些实物能抽象出什么样的几何图形?
——角
线段
射线
直线
你能根据这个图形给出角的定义吗?
想一想:
有公共端点的两条射线组成的图形叫做角。
定义:
静态
边
顶点
边
公共端点
1.判断下列哪些图形是角?
(√)
(×)
(√)
(×)
思考:
2.下列说法是否正确,如果不正确,请说出错在哪里?
(×)
(×)
⑴
两条有公共端点的线段组成的图形叫角;
⑵
两条有公共点的射线组成的图形叫角。
思考:
O
A
B
始边OA与终边OB组成什么图形?
角
旋转
想一想:
O
A
B
角也可以看作由一条射线绕着它的端点旋转形成的图形。
定义:
动态
当射线旋转到与始边成一条直线时,形成
角。
当射线旋转到与始边重合时,形成
角。
平
周
O
A
B
O
A
(B)
角也可以看成是由一条射线绕着它的端点旋转而形成的图形。
有公共端点的两条射线所组成的图形叫做角。
定义:
O
A
B
·
A
O
B
第二个定义:
始边
终边
当始边OA与终边OB成一直线时形成了平角
180°
当始边OA与终边OB重合时形成了周角
360°
注意:无特别说明,我们
指的角是小于平角的角
静
动
归纳:
一共有哪些表示角的方法?
想一想:
∠α
O
A
B
①
①
用三个大写字母表示:
∠AOB
或
∠BOA
②
用顶点的大写字母表示:
③
用一个希腊字母表示:
④
用一个阿拉伯数字表示:
∠O
∠1
O
②
α
③
1
④
表示方法
注意事项
①用三个大写字母表示
表示顶点的字母要写在中间
②用顶点的大写字母表示
顶点处只有一个角
③用一个希腊字母表示
在靠近顶点的处画弧线,并写上希腊字母
④用一个阿拉伯数字表示
在靠近顶点的处画弧线,并写上数字
A
B
O
思考:
1.如图,还能把∠AOB
记作∠O
吗?为什么?
C
2.图中你还能找到哪些角,怎么表示呢?
∠AOC
和∠BOC
这是1°角
1°=60'
1''=
'
1′=60″
1'=
°
由此,我们可以得到度、分、秒是
进制的。
60
角的基本度量单位:
度、分、秒
分、秒的定义:
把
的角等分成60份,
①
②
把
的角等分成60份,
即:
角的度量工具:
量角器
类比
时间单位
每一份就是1分,记作
每一份就是1秒,记作
(60进制)
1周角
1平角
1直角
角的基本度量单位:
度、分、秒
1周角
=360°
=180°
=90
°
=2平角
=4直角
度
分秒
不足1度的化成分
不足1分的化成秒
分秒
度
秒
分
度
1°=60
′=3600
″
1.
度到分的换算
【例1】
1°=60'
1°是一个60′
2°是
个60′
两
即:2°=2×60′=120′
1′=60″
0.5′=
×
=
。
1′是一个
;
2′是
个
;
即:2′=2×
=
;
2.
分到秒的换算
两
60″
60″
60″
120″
30″
0.5
60″
【例2】
3.
分到度的换算
两
1′=
°
1′是一个
°
2′是
个
°
即:2′=2×
°=
°
【例3】
4.
秒到分的换算
2″是
个
′
两
1″=
′
1″是一个
′
即:2″=2×
′=
′
【例4】
2
二、典型例题
度分秒的互化
(1)
57.32°=
°
′
″;
解析:57.32?=57?+0.32×60′
=57?+19.2′
=57?19′+0.2×60″
=57?19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒.
(小数化整数)
57
19
12
【例1】
(2)
17°6′36″=
°.
17.11
解析:17°6′36″=17°+6′+
′′
=17°+6.6′
=17?+
°
=17.11?.
按1″=
′,1′=
°先把秒化成分,再把分化成度.
(整数化小数)
【例1】
300
18000
38
9
0.6
0.01
38.25
5°= ′=
″;38.15°= ° ′;36″= ′= °;
38°15′= °.
【例1】
如图,时钟显示为10:10时,时针与分针所夹
角度是
( )
A.90°
B.100°
C.105°
D.115°
解析:时针每小时旋转的夹角360°
÷12=30°,故10分钟,时针旋转的角度为5°,即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
【例2】
3
三、课堂练习
2.如图,其中小于180°的角共有(
)
1.教材P134 练习第1,2,3题.
练
习
C
A.3个
B.4个
C.5个
D.6个
3.若∠1=25°12′,∠2=25.12°,∠3=25.2°,则下列结论正确的是(
)
A.∠1=∠2
B.∠2=∠3
C.∠1=∠3
D.∠1=∠2=∠3
练
习
C
4.分别确定四个城市相应钟表上时针与分针所成的小于平角的角的度数,并填在相应的横线上.
巴黎时间
北京时间
伦敦时间
东京时间
30°
120°
0°
90°
练
习
练
习
5.如图,一共有多少个小于平角东京时间的角?按图中字母把它们表示出来,并指出哪些角可以用一个字母表示.
解:图中一共有14个小于平角的角,用字母表示为:∠ABF,∠FBD,∠ABD,∠ACB,∠ACF,∠FCD,∠BCF,∠ACD,∠AEB,∠BEC,∠CEF,∠AEF,∠A,∠F,其中∠A和∠F可用一个字母表示.
角的定义
有公共端点的两条射线组成的图形
一条射线绕着它的端点旋转而形成的图形
角的表示方法
用三个大写字母或一个大写字母表示
用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量
度、分、秒
1°=60′,1′=60″
谢
谢
!
