数学人教版八年级 上册课件 15.3分式方程(第二课时)课件(25张)
文档属性
| 名称 | 数学人教版八年级 上册课件 15.3分式方程(第二课时)课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 288.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 17:21:24 | ||
图片预览







文档简介
(共25张PPT)
分式方程(第二课时)
知识回顾
分式方程的概念:
分母中含有未知数的方程,叫做分式方程.
解分式方程时通过去分母将分式方程转化为整式方程,体会到将未知转化为已知,复杂转化为简单的化归思想.
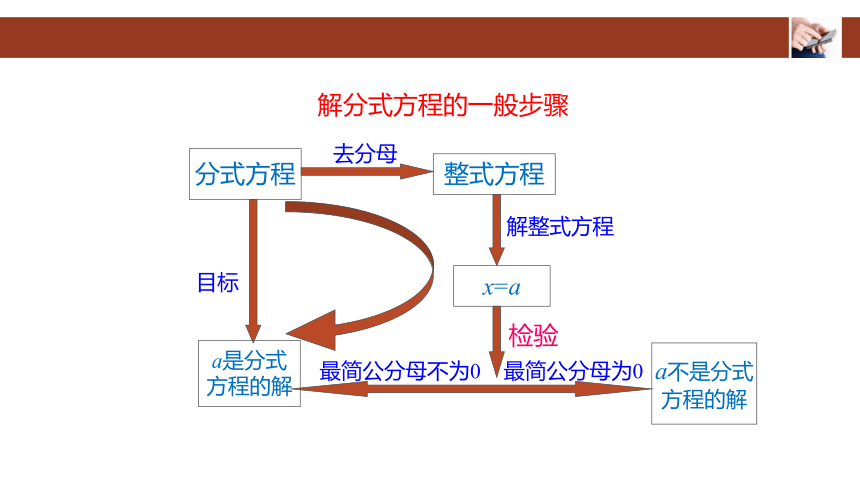
解分式方程的一般步骤
分式方程
整式方程
x=a
a不是分式
方程的解
a是分式
方程的解
最简公分母不为0
最简公分母为0
检验
解整式方程
去分母
目标
解分式方程
分析:方程两边乘(x+1)(x-1)
最简公分母为(x+1)(x-1)
(x+1)(x-1)
解分式方程
解:方程两边乘(x+1)(x-1),得
解得
检验:当x=1
时,(x+1)(x-1)=0.
∴原分式方程无解.
最简公分母为(x+1)(x-1)
例
解下列分式方程:
(2)
(1)
分析:
原方程可化为
最简公分母为x(x+1)(x-1)
(1)
分母是多项式
分解因式
例
解下列分式方程:
检验:当
时
,x(x+1)(x-1)≠0.
∴
是原分式方程的解.
解得
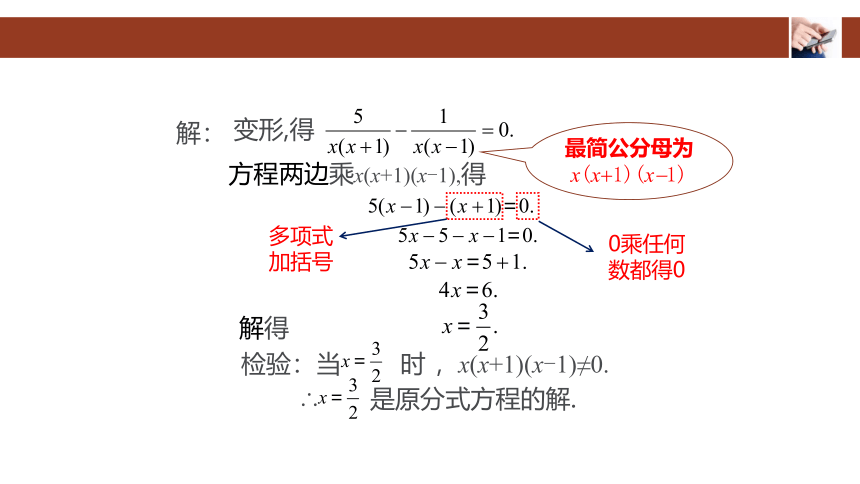
变形,得
最简公分母为x(x+1)(x-1)
方程两边乘x(x+1)(x-1),得
解:
0乘任何数都得0
多项式加括号
解:
变形,得
整理,得
最简公分母为(y+2)(y-2)
(2)
例
解下列分式方程:
方程两边乘
,得
整理,得
最简公分母为(y+2)(y-2)
检验:当
时,
≠0.
∴
是原分式方程的解.
解得
整理,得
最简公分母为(y+2)(y-2)
小结
①当分式方程中含有可分解因式的多项式时,先将其进行因式分解,可方便确定最简公分母;
③去分母后是多项式时,一定要加括号;
②分母因式分解后,观察分式的分子和分母,能约分的要先约分,可方便计算;
④解分式方程一定要检验.
练习
解下列分式方程:
(1)
;
(2)
;
(3)
.
变形,得
解:
最简公分母为(x+2)(x-2)
(1)
;
练习
解下列分式方程:
方程两边乘(x+2)(x-2),得
最简公分母为(x+2)(x-2)
变形,得
不要漏乘不含分母的项
解得
检验:当x=-2时,(x+2)(x-2)=0.
∴原分式方程无解.
最简公分母为(x+2)(x-2)
.
变形,得
变形,得
解:
最简公分母为x(x+1)(x-1)
(2)
;
练习
解下列分式方程:
变形,得
最简公分母为x(x+1)(x-1)
方程两边乘x(x+1)(x-1),得
变形,得
最简公分母为x(x+1)(x-1)
检验:当x=3时,x(x+1)(x-1)≠0.
∴x=3是原分式方程的解.
解得
变形,得
解:
最简公分母为(x+4)(x-4)
(3)
.
练习
解下列分式方程:
互为相反数
变形,得
最简公分母为(x+4)(x-4)
方程两边乘(x+4)(x-4),得
解得
检验:当
时,(x+4)(x-4)≠0.
∴
是原分式方程的解.
变形,得
最简公分母为(x+4)(x-4)
课堂小结
1.解较复杂分式方程时,先变形整理,能约分的先约分,可方便确定最简公分母;
2.最简公分母的确定方法;
3.注意每一步变形都要有依据,去分母时,不要漏乘不含分母的项;
4.分式方程一定要检验.
课后作业
解方程:(1)
;
(2)
;
(3)
同学们,再见!
分式方程(第二课时)
知识回顾
分式方程的概念:
分母中含有未知数的方程,叫做分式方程.
解分式方程时通过去分母将分式方程转化为整式方程,体会到将未知转化为已知,复杂转化为简单的化归思想.
解分式方程的一般步骤
分式方程
整式方程
x=a
a不是分式
方程的解
a是分式
方程的解
最简公分母不为0
最简公分母为0
检验
解整式方程
去分母
目标
解分式方程
分析:方程两边乘(x+1)(x-1)
最简公分母为(x+1)(x-1)
(x+1)(x-1)
解分式方程
解:方程两边乘(x+1)(x-1),得
解得
检验:当x=1
时,(x+1)(x-1)=0.
∴原分式方程无解.
最简公分母为(x+1)(x-1)
例
解下列分式方程:
(2)
(1)
分析:
原方程可化为
最简公分母为x(x+1)(x-1)
(1)
分母是多项式
分解因式
例
解下列分式方程:
检验:当
时
,x(x+1)(x-1)≠0.
∴
是原分式方程的解.
解得
变形,得
最简公分母为x(x+1)(x-1)
方程两边乘x(x+1)(x-1),得
解:
0乘任何数都得0
多项式加括号
解:
变形,得
整理,得
最简公分母为(y+2)(y-2)
(2)
例
解下列分式方程:
方程两边乘
,得
整理,得
最简公分母为(y+2)(y-2)
检验:当
时,
≠0.
∴
是原分式方程的解.
解得
整理,得
最简公分母为(y+2)(y-2)
小结
①当分式方程中含有可分解因式的多项式时,先将其进行因式分解,可方便确定最简公分母;
③去分母后是多项式时,一定要加括号;
②分母因式分解后,观察分式的分子和分母,能约分的要先约分,可方便计算;
④解分式方程一定要检验.
练习
解下列分式方程:
(1)
;
(2)
;
(3)
.
变形,得
解:
最简公分母为(x+2)(x-2)
(1)
;
练习
解下列分式方程:
方程两边乘(x+2)(x-2),得
最简公分母为(x+2)(x-2)
变形,得
不要漏乘不含分母的项
解得
检验:当x=-2时,(x+2)(x-2)=0.
∴原分式方程无解.
最简公分母为(x+2)(x-2)
.
变形,得
变形,得
解:
最简公分母为x(x+1)(x-1)
(2)
;
练习
解下列分式方程:
变形,得
最简公分母为x(x+1)(x-1)
方程两边乘x(x+1)(x-1),得
变形,得
最简公分母为x(x+1)(x-1)
检验:当x=3时,x(x+1)(x-1)≠0.
∴x=3是原分式方程的解.
解得
变形,得
解:
最简公分母为(x+4)(x-4)
(3)
.
练习
解下列分式方程:
互为相反数
变形,得
最简公分母为(x+4)(x-4)
方程两边乘(x+4)(x-4),得
解得
检验:当
时,(x+4)(x-4)≠0.
∴
是原分式方程的解.
变形,得
最简公分母为(x+4)(x-4)
课堂小结
1.解较复杂分式方程时,先变形整理,能约分的先约分,可方便确定最简公分母;
2.最简公分母的确定方法;
3.注意每一步变形都要有依据,去分母时,不要漏乘不含分母的项;
4.分式方程一定要检验.
课后作业
解方程:(1)
;
(2)
;
(3)
同学们,再见!
