2.4 等比数列
图片预览





文档简介
(共14张PPT)
(1)如果一个数列从第___项起,每一项与它的____ _ 的比等于____ _常数 q,这个数列叫做____________ ,
q为此数列的_____,即q = 或
(2)由三个数a,G,c组成的等比数列中,中间的数G叫做a
与c的 , , 则 a,c必须
,两个数有 等比中项,即
(3)等比数列的通项公式为:
二
前一项
同一
等比数列
公比
等比中项
=
同号
两个
知识与技能
理解等差比数列的概念;探索并掌握等比数列的通项公式;能在具体的问题情境中,发现数列的等比关系并能用有关知识解决相应的问题。
过程与方法
体会猜想与总结的过程,体会从特殊到一般的方法和对比的方法。
情感态度与价值观
通过学生之间、师生之间的交流与配合培养学生的合作意识和团队精神;也使学生体会等比、等差的相似美,结构美,增强他们对数学学习的自信心和对数学的情感.
1.某种细胞分裂的过程:
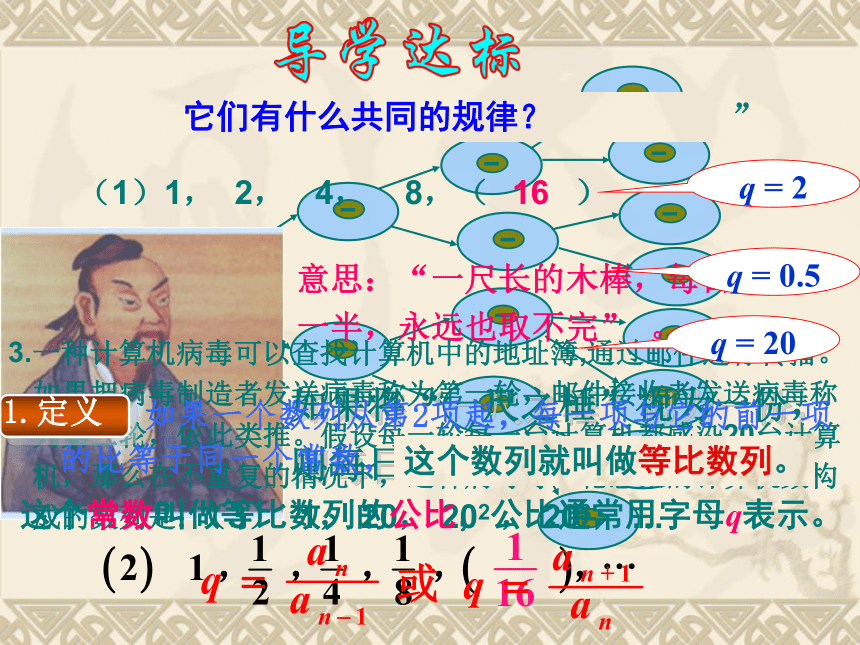
(1)1, 2, 4, 8,( )
16
2. 庄子曰:“一尺之棰,日取其半,万世不竭.”
意思:“一尺长的木棒,每日取其一半,永远也取不完” 。
如果将“一尺之棰”视为一份,
则每日剩下的部分依次为:
3.一种计算机病毒可以查找计算机中的地址簿,通过邮件进行传播。如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推。假设每一轮每一台计算机都感染20台计算机,那么在不重复的情况下,这种病毒每一轮感染的计算机数构成的数列是:
(3) 1, 20, 202 , 203, …
它们有什么共同的规律?
1.定义:如果一个数列从第2项起,每一项与它的前一项
的比等于同一个常数,
这个常数叫做等比数列的公比,公比通常用字母q表示。
这个数列就叫做等比数列。
q = 2
q = 0.5
q = 20
1.定义
(1) 1,3,9,27,81,…
(3) 5,5,5,5,5,5,…
(4) 1,-1,1,-1,1,…
是,公比 q = 3
是,公比 q = x
是,公 比q = -1
(7)
(2)
是,公比
观察并判断下列数列是否是等比数列:
是,公比 q =1
(5) 1,0,1,0,1,…
(6) 0,0,0,0,0,…
不是等比数列
不是等比数列
(1) 1,3,9,27,…
(3) 5, 5, 5, 5,…
(4) 1,-1,1,-1,…
(2)
(5) 1,0,1,0,…
(6) 0,0,0,0,…
1. 各项不能为零,即
2. 公比不能为零,即
4. 常数数列a,a,a,a,…
时,既是等差数列
又是等比数列;
时,只是等差数列
而不是等比数列.
3. 当q>0,各项与首项同号
当q<0,各项符号正负交替
对概念的更深理解
2. 通项公式
… …
方法一:递推法
方法二:叠乘法
… …
(n -1)个 式子
以上各式相乘得:
公式一:
公式二:
已知任意两项求公比
① n-m为奇数,
② n-m为偶数,
3.等比数列与函数的关系
画出等比数列 an=2n-1的图象和函数 y =2x-1的图象,探究它们的关系。
几何画板演示
等比数列的图象是指数函数图象上一群孤立点
例1、某种放射性物质不断变化为其他物质,每经过一年剩留的这种物质是原来的84﹪,这种物质的半衰期为多长(精确到1年)?
经过1年
0.84
经过2年
0.84×0.84
0.842
经过3年
0.843
经过n年
0.84n
…
…
则
两边取常用对数
则
解:依题意可建立等比数列{an}
答:这种物质的半衰期大约为4年
例2、根据右图的框图,写出所打印数列的前5项,并建立数列的递推公式.这个数列是等比数列吗
是
开始
A=1
n=1
A= A
n=n+1
n>5
输出A
结束
否
解:
∴这个数列是等比数列
例3 一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项.
解得
答:这个数列的第1项与第2项分别是 与 8.
解法一:由题意得
解法二:由题意得
P52 1)已知{an}是一个等差数列,填下表
a1 a3 a5 a7 q
2 8
2 0.2
4
16
50
0.08
0.0032
(1)一个等比数列的第5项是 ,公比是 ,则它的第
1项是 。
(2)一个等比数列的第2项是10,第3项是20,则它的第
1项是 ,第4项是 .
36
5
40
课本 P53 习题 A 1,7,8
金榜测评 2.4 相应练习
预习 必修5 2.4 等比数列(2)
家庭作业
(1)如果一个数列从第___项起,每一项与它的____ _ 的比等于____ _常数 q,这个数列叫做____________ ,
q为此数列的_____,即q = 或
(2)由三个数a,G,c组成的等比数列中,中间的数G叫做a
与c的 , , 则 a,c必须
,两个数有 等比中项,即
(3)等比数列的通项公式为:
二
前一项
同一
等比数列
公比
等比中项
=
同号
两个
知识与技能
理解等差比数列的概念;探索并掌握等比数列的通项公式;能在具体的问题情境中,发现数列的等比关系并能用有关知识解决相应的问题。
过程与方法
体会猜想与总结的过程,体会从特殊到一般的方法和对比的方法。
情感态度与价值观
通过学生之间、师生之间的交流与配合培养学生的合作意识和团队精神;也使学生体会等比、等差的相似美,结构美,增强他们对数学学习的自信心和对数学的情感.
1.某种细胞分裂的过程:
(1)1, 2, 4, 8,( )
16
2. 庄子曰:“一尺之棰,日取其半,万世不竭.”
意思:“一尺长的木棒,每日取其一半,永远也取不完” 。
如果将“一尺之棰”视为一份,
则每日剩下的部分依次为:
3.一种计算机病毒可以查找计算机中的地址簿,通过邮件进行传播。如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推。假设每一轮每一台计算机都感染20台计算机,那么在不重复的情况下,这种病毒每一轮感染的计算机数构成的数列是:
(3) 1, 20, 202 , 203, …
它们有什么共同的规律?
1.定义:如果一个数列从第2项起,每一项与它的前一项
的比等于同一个常数,
这个常数叫做等比数列的公比,公比通常用字母q表示。
这个数列就叫做等比数列。
q = 2
q = 0.5
q = 20
1.定义
(1) 1,3,9,27,81,…
(3) 5,5,5,5,5,5,…
(4) 1,-1,1,-1,1,…
是,公比 q = 3
是,公比 q = x
是,公 比q = -1
(7)
(2)
是,公比
观察并判断下列数列是否是等比数列:
是,公比 q =1
(5) 1,0,1,0,1,…
(6) 0,0,0,0,0,…
不是等比数列
不是等比数列
(1) 1,3,9,27,…
(3) 5, 5, 5, 5,…
(4) 1,-1,1,-1,…
(2)
(5) 1,0,1,0,…
(6) 0,0,0,0,…
1. 各项不能为零,即
2. 公比不能为零,即
4. 常数数列a,a,a,a,…
时,既是等差数列
又是等比数列;
时,只是等差数列
而不是等比数列.
3. 当q>0,各项与首项同号
当q<0,各项符号正负交替
对概念的更深理解
2. 通项公式
… …
方法一:递推法
方法二:叠乘法
… …
(n -1)个 式子
以上各式相乘得:
公式一:
公式二:
已知任意两项求公比
① n-m为奇数,
② n-m为偶数,
3.等比数列与函数的关系
画出等比数列 an=2n-1的图象和函数 y =2x-1的图象,探究它们的关系。
几何画板演示
等比数列的图象是指数函数图象上一群孤立点
例1、某种放射性物质不断变化为其他物质,每经过一年剩留的这种物质是原来的84﹪,这种物质的半衰期为多长(精确到1年)?
经过1年
0.84
经过2年
0.84×0.84
0.842
经过3年
0.843
经过n年
0.84n
…
…
则
两边取常用对数
则
解:依题意可建立等比数列{an}
答:这种物质的半衰期大约为4年
例2、根据右图的框图,写出所打印数列的前5项,并建立数列的递推公式.这个数列是等比数列吗
是
开始
A=1
n=1
A= A
n=n+1
n>5
输出A
结束
否
解:
∴这个数列是等比数列
例3 一个等比数列的第3项与第4项分别是12与18,求它的第1项与第2项.
解得
答:这个数列的第1项与第2项分别是 与 8.
解法一:由题意得
解法二:由题意得
P52 1)已知{an}是一个等差数列,填下表
a1 a3 a5 a7 q
2 8
2 0.2
4
16
50
0.08
0.0032
(1)一个等比数列的第5项是 ,公比是 ,则它的第
1项是 。
(2)一个等比数列的第2项是10,第3项是20,则它的第
1项是 ,第4项是 .
36
5
40
课本 P53 习题 A 1,7,8
金榜测评 2.4 相应练习
预习 必修5 2.4 等比数列(2)
家庭作业
