江苏省常州市武进区礼嘉中学2020-2021学年高一上学期第二次阶段教学质量调研数学试题word版含答案
文档属性
| 名称 | 江苏省常州市武进区礼嘉中学2020-2021学年高一上学期第二次阶段教学质量调研数学试题word版含答案 | 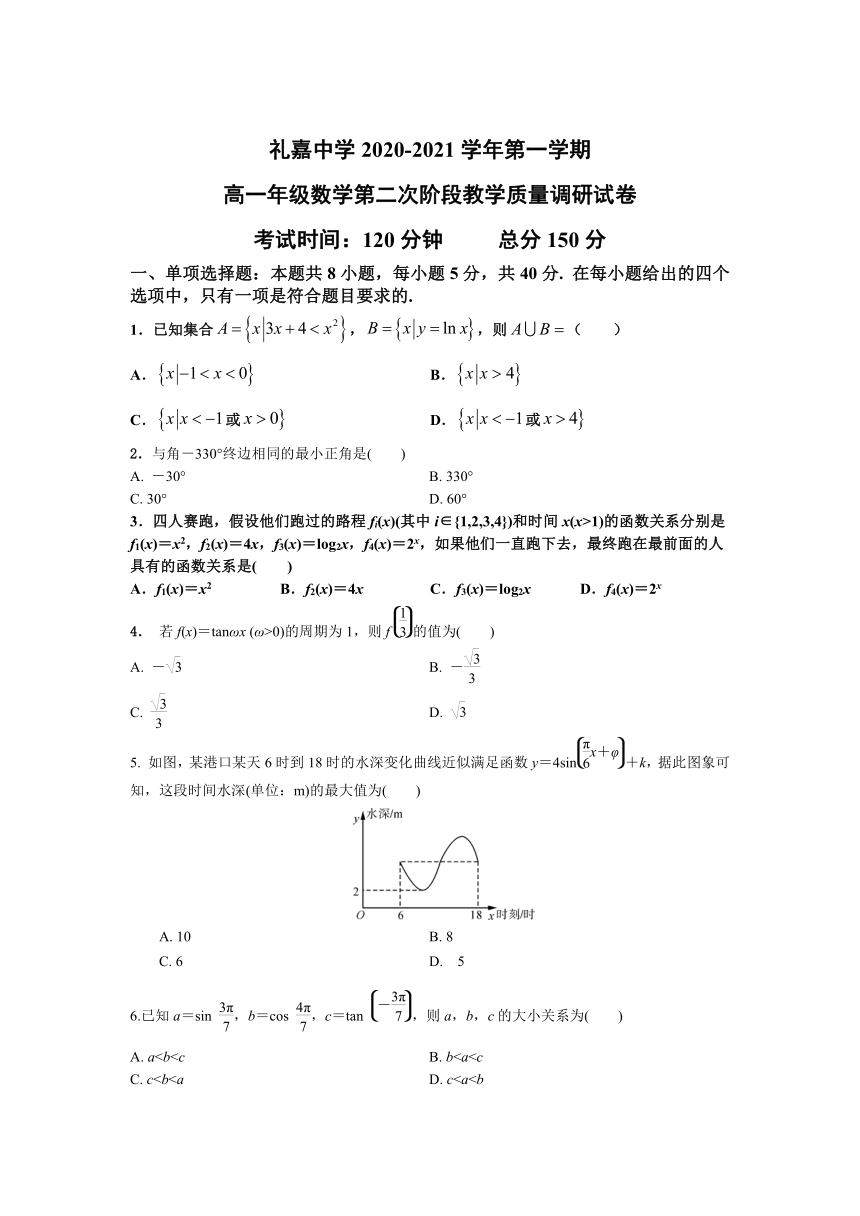 | |
| 格式 | zip | ||
| 文件大小 | 365.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 16:36:31 | ||
图片预览




文档简介
礼嘉中学2020-2021学年第一学期
高一年级数学第二次阶段教学质量调研试卷
考试时间:120分钟
总分150分
一、单项选择题:本题共8小题,每小题5分,共40分.
在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则(
)
A.
B.
C.或
D.或
2.与角-330°终边相同的最小正角是( )
A.
-30°
B.
330°
C.
30°
D.
60°
3.四人赛跑,假设他们跑过的路程fi(x)(其中i∈{1,2,3,4})和时间x(x>1)的函数关系分别是f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x,如果他们一直跑下去,最终跑在最前面的人具有的函数关系是( )
A.f1(x)=x2
B.f2(x)=4x
C.f3(x)=log2x
D.f4(x)=2x
4.
若f(x)=tanωx
(ω>0)的周期为1,则f的值为( )
A.
-
B.
-
C.
D.
5.
如图,某港口某天6时到18时的水深变化曲线近似满足函数y=4sin+k,据此图象可知,这段时间水深(单位:m)的最大值为( )
A.
10
B.
8
C.
6
D.
5
6.已知a=sin
,b=cos
,c=tan
,则a,b,c的大小关系为( )
A.
aB.
bC.
cD.
c7.若,,则(
)
A.-1
B.0
C.1
D.2
8.在同一平面直角坐标系中,函数y=ax+a与y=ax(a>0且a≠1)的图象大致是( )
二、多项选择题:本题共4小题,每小题5分,共20分.
在每小题给出的选项中,有多项符合题目要求的.
全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列函数在区间(0,1)上单调递减的函数有( )
A.
y=x
B.
u=log(x+1)
C.
y=|x-1|
D.
y=2x+1
10.下列函数中,以为周期且图象关于x=对称的是( )
A.
y=sin
|x|
B.
y=cos
|x|
C.
y=|sin
2x|
D.
y=|cos
2x|
11.若0A.
0B.
3y<3x
C.
log4xD.
logx312.对于函数f(x)=3sin的图象为C,下列叙述正确的是( )
A.
图象C关于直线x=π对称
B.
函数f(x)在区间内是增函数
C.
由y=3sin
2x的图象向右平移个单位长度可以得到图象C
D.
图象C关于点对称
三、填空题:本题共4小题,每小题5分,共20分.
13.若扇形的圆心角为2
rad,面积为4
cm2,则该扇形的半径为________cm.
14.
已知幂函数f(x)的图象过点,则这个函数的解析式为________;若f=2,则a的值为________.(第一空2分,第二空3分)
15.
函数y=loga(x+3)-1(a>0且a≠1)的图象恒过定点A,若点A在一次函数y=-x-的图象上,其中mn>0,则+的最小值为________.
16.已知cos=,则cos-sin
2=________.
四、解答题:本题共6个小题,共70分.
解答应写出文字说明、证明过程或演算步骤.
17.已知,且是第________象限角.
从①一,②二,③三,④四,这四个选项中选择一个你认为恰当的选项填在上面的横线上,并根据你的选择,解答以下问题:
(1)求的值;
(2)化简求值:.
18.已知函数f(x)=lg(x-1),g(x)=lg(4-x).
(1)
求函数h(x)=f(x)-g(x)的定义域;
(2)
求不等式f(x)>g(x)成立时,实数x的取值范围.
19.在平面直角坐标系xOy中,以Ox
轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知点A,B的横坐标分别为,.
(1)
求cos
α和sin
β的值;
(2)
求的值.
20.已知函数f(x)=1+为奇函数.
(1)
求a的值,并证明:f(x)是R上的增函数;
(2)
若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
21.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),它的部分图象如图所示.
(1)
求函数f(x)的解析式;
(2)
将函数f(x)图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位长度,得到函数g(x)的图象,求当x∈时,函数g(x)的单调递增区间.
22.某企业参加项目生产的工人为人,平均每人每年创造利润万元.根据现实的需要,从项目中调出人参与项目的售后服务工作,每人每年可以创造利润万元(),项目余下的工人每人每年创造利图需要提高
(1)若要保证项目余下的工人创造的年总利润不低于原来名工人创造的年总利润,则最多调出多少人参加项目从事售后服务工作?
(2)在(1)的条件下,当从项目调出的人数不能超过总人数的时,才能使得项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数的取值范围.
1.
【答案】C
【详解】
或,,
∴或.
故选:C.
2.
【解析】C 与角-330°终边相同的最小正角为-330°+360°=30°.故选C.
3.
【答案】D
【解析】
由函数的增长趋势可知,指数函数增长最快,所以最终最前面的具有的函数关系为,故选D.
4.
【解析】D 依题意T==1,ω=π,所以f(x)=tan,所以f=tan
=.故选D.
5.
A 【解析】 某港口某天6时到18时的水深变化曲线近似满足函数y=4sin+k,据此图象可知,这段时间水深最小值为-4+k=2,所以k=6,故这段时间水深的最大值为4+6=10,故选A.
6.
【解析】C 因为是一个锐角,故a=sin
>0;又cos
,故-1,而<<,故c<-1.综上,c7.
【答案】A
【分析】
令,解得,得到,进而求得的值.
【详解】
由题意,函数,令,解得,即
又由函数,可得.
故选:A.
8.
【解析】B 指数函数y=ax(a>0且a≠1)的图象恒过点(0,1),一次函数y=ax+a=a(x+1)的图象恒过点(-1,0),图象与y轴的交点为(0,a).A中由指数函数图象可得a>1,由一次函数图象可得01,矛盾;D中直线不经过点(-1,0),不符合.故选B.
9.【解析】BC A是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求;B中的函数是由函数y=logx向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;C中的函数图象是由函数y=x-1的图象保留x轴上方,下方图象翻折到x轴上方而得到的,故由其图象可知该项符合要求;D中的函数图象为指数函数y=2x的图象向左平移1个单位长度得到,因其底数大于1,故其在R上单调递增,不合题意.故选BC.
10
【解析】
CD 对于A选项,y=f=sin=≠1,所以y=sin|x|的图象不关于x=对称,故A错误;对于B选项,y=cos|x|=cos
x,由余弦函数的图象可知,x=不是其对称轴,故B错误;对于C选项,函数y=|sin
2x|的周期为T=,y=f==1,由其函数图象知,x=是其对称轴,故C正确;对于D选项,函数y=|cos
2x|的周期为T=,y=f==0,由其函数图象知,x=是其对称轴,故D正确.故选CD.
11.
【解析】AC 因为y=log4x在(0,+∞)上单调递增,且03x,故B错误;取x=,y=,知logx3>logy3,故D错误.故选AC.
12.
【解析】 AB 把x=π代入,f(x)=3sin=3sinπ=-3,取得最小值,所以x=π为对称轴,A正确;令2kπ-≤2x-≤2kπ+(k∈Z),解得kπ-≤kπ+(k∈Z),当k=0时,增区间为,B正确;y=3sin
2x的图象向右平移个单位长度可以得到图象C:y=3sin=3sin,所以C错误,把代入,f(x)=3sin=3sin≠0,y的值不为0,所以D错误.故选AB.
三、填空题:本题共4小题,每小题5分,共20分.
13.【解析】2 设扇形的圆心角大小为α(rad),半径为r.由题意可得,扇形的面积S=αr2,即4=×2×r2,解得r=2.
14.
【解析】
f(x)= 4 设函数f(x)=xm,则f(3)=3m=?m=,所以f(x)=x=.f(a)==2?a=4.
15.
【解析】3+2 由题意可知,令x+3=1,则y=-1,即x=-2,y=-1,所以A(-2,-1),可得2m+n=1,所以+==3++≥3+2,当且仅当,即时,等号成立,所以+的最小值为3+2.
16.【解析】- cos-sin2=cos-sin2=-cos-sin2=-cos+cos2-1=-+-1=-.
四、解答题:本题共6个小题,共70分.
解答应写出文字说明、证明过程或演算步骤.
17.
.
【详解】
(1)因为,所以为第三象限或第四象限角;
若选③,;
若选④,;
(2)原式.
18.
【详解】
(1)
f(x)=lg(x-1)的定义域为(1,+∞),g(x)=lg(4-x)的定义域为(-∞,4),所以函数h(x)=f(x)-g(x)的定义域为(1,4).
(2)
不等式f(x)>g(x),等价于lg(x-1)>lg(4-x),即x-1>4-x,解得x>.
又定义域为(1,4),所以实数x的取值范围为.
19.
【详解】
(1)
由已知条件及三角函数的定义可知,cos
α=,cos
β=,因为α为锐角,故sin
α>0,从而sin
α==;因为β为锐角,故sin
β>0,从而sin
β==.
(2)
==-=-=-.
20.
【详解】
(1)
因为f(x)定义在R上的奇函数,所以f(0)=0,得a=-2.此时f(x)=1-=,f(-x)===-f(x),所以f(x)是奇函数,所以a=-2.任取x1,x2∈R,且x1<0,所以f(x1)(2)
因为f(x)为奇函数,f(t2-2t)+f(2t2-k)<0的解集非空,所以f(t2-2t)0,即(-2)2+12k>0,解得k>-,即k的取值范围为.
21.
(1)
由图可知,A=2,=-=,则T=π,所以ω=2,由2×+φ=+2kπ,|φ|<π,得φ=-,所以f(x)=2sin.
(2)
将函数f(x)图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得y=2sin,再将得到的图象向左平移个单位长度,得到函数g(x)=2sin,令-+2kπ≤x+≤+2kπ,解得-+2kπ≤x≤+2kπ,k∈Z.取k=0,可得-≤x≤,所以函数y=g(x)在x∈上的单调递增区间为.
22.
【详解】
设调出人参加项目从事售后服务工作
(1)由题意得:,
即,又,所以.即最多调整500名员工从事第三产业.
(2)由题知,,
从事第三产业的员工创造的年总利润为万元,
从事原来产业的员工的年总利润为万元,
则,
所以,
所以,即恒成立,
因为,所以,所以,
又,所以,即的取值范围为.
高一年级数学第二次阶段教学质量调研试卷
考试时间:120分钟
总分150分
一、单项选择题:本题共8小题,每小题5分,共40分.
在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则(
)
A.
B.
C.或
D.或
2.与角-330°终边相同的最小正角是( )
A.
-30°
B.
330°
C.
30°
D.
60°
3.四人赛跑,假设他们跑过的路程fi(x)(其中i∈{1,2,3,4})和时间x(x>1)的函数关系分别是f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x,如果他们一直跑下去,最终跑在最前面的人具有的函数关系是( )
A.f1(x)=x2
B.f2(x)=4x
C.f3(x)=log2x
D.f4(x)=2x
4.
若f(x)=tanωx
(ω>0)的周期为1,则f的值为( )
A.
-
B.
-
C.
D.
5.
如图,某港口某天6时到18时的水深变化曲线近似满足函数y=4sin+k,据此图象可知,这段时间水深(单位:m)的最大值为( )
A.
10
B.
8
C.
6
D.
5
6.已知a=sin
,b=cos
,c=tan
,则a,b,c的大小关系为( )
A.
a
b
c
c
)
A.-1
B.0
C.1
D.2
8.在同一平面直角坐标系中,函数y=ax+a与y=ax(a>0且a≠1)的图象大致是( )
二、多项选择题:本题共4小题,每小题5分,共20分.
在每小题给出的选项中,有多项符合题目要求的.
全部选对的得5分,部分选对的得3分,有选错的得0分.
9.下列函数在区间(0,1)上单调递减的函数有( )
A.
y=x
B.
u=log(x+1)
C.
y=|x-1|
D.
y=2x+1
10.下列函数中,以为周期且图象关于x=对称的是( )
A.
y=sin
|x|
B.
y=cos
|x|
C.
y=|sin
2x|
D.
y=|cos
2x|
11.若0
0
3y<3x
C.
log4x
logx3
A.
图象C关于直线x=π对称
B.
函数f(x)在区间内是增函数
C.
由y=3sin
2x的图象向右平移个单位长度可以得到图象C
D.
图象C关于点对称
三、填空题:本题共4小题,每小题5分,共20分.
13.若扇形的圆心角为2
rad,面积为4
cm2,则该扇形的半径为________cm.
14.
已知幂函数f(x)的图象过点,则这个函数的解析式为________;若f=2,则a的值为________.(第一空2分,第二空3分)
15.
函数y=loga(x+3)-1(a>0且a≠1)的图象恒过定点A,若点A在一次函数y=-x-的图象上,其中mn>0,则+的最小值为________.
16.已知cos=,则cos-sin
2=________.
四、解答题:本题共6个小题,共70分.
解答应写出文字说明、证明过程或演算步骤.
17.已知,且是第________象限角.
从①一,②二,③三,④四,这四个选项中选择一个你认为恰当的选项填在上面的横线上,并根据你的选择,解答以下问题:
(1)求的值;
(2)化简求值:.
18.已知函数f(x)=lg(x-1),g(x)=lg(4-x).
(1)
求函数h(x)=f(x)-g(x)的定义域;
(2)
求不等式f(x)>g(x)成立时,实数x的取值范围.
19.在平面直角坐标系xOy中,以Ox
轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知点A,B的横坐标分别为,.
(1)
求cos
α和sin
β的值;
(2)
求的值.
20.已知函数f(x)=1+为奇函数.
(1)
求a的值,并证明:f(x)是R上的增函数;
(2)
若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
21.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),它的部分图象如图所示.
(1)
求函数f(x)的解析式;
(2)
将函数f(x)图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位长度,得到函数g(x)的图象,求当x∈时,函数g(x)的单调递增区间.
22.某企业参加项目生产的工人为人,平均每人每年创造利润万元.根据现实的需要,从项目中调出人参与项目的售后服务工作,每人每年可以创造利润万元(),项目余下的工人每人每年创造利图需要提高
(1)若要保证项目余下的工人创造的年总利润不低于原来名工人创造的年总利润,则最多调出多少人参加项目从事售后服务工作?
(2)在(1)的条件下,当从项目调出的人数不能超过总人数的时,才能使得项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数的取值范围.
1.
【答案】C
【详解】
或,,
∴或.
故选:C.
2.
【解析】C 与角-330°终边相同的最小正角为-330°+360°=30°.故选C.
3.
【答案】D
【解析】
由函数的增长趋势可知,指数函数增长最快,所以最终最前面的具有的函数关系为,故选D.
4.
【解析】D 依题意T==1,ω=π,所以f(x)=tan,所以f=tan
=.故选D.
5.
A 【解析】 某港口某天6时到18时的水深变化曲线近似满足函数y=4sin+k,据此图象可知,这段时间水深最小值为-4+k=2,所以k=6,故这段时间水深的最大值为4+6=10,故选A.
6.
【解析】C 因为是一个锐角,故a=sin
>0;又cos
【答案】A
【分析】
令,解得,得到,进而求得的值.
【详解】
由题意,函数,令,解得,即
又由函数,可得.
故选:A.
8.
【解析】B 指数函数y=ax(a>0且a≠1)的图象恒过点(0,1),一次函数y=ax+a=a(x+1)的图象恒过点(-1,0),图象与y轴的交点为(0,a).A中由指数函数图象可得a>1,由一次函数图象可得0
9.【解析】BC A是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求;B中的函数是由函数y=logx向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;C中的函数图象是由函数y=x-1的图象保留x轴上方,下方图象翻折到x轴上方而得到的,故由其图象可知该项符合要求;D中的函数图象为指数函数y=2x的图象向左平移1个单位长度得到,因其底数大于1,故其在R上单调递增,不合题意.故选BC.
10
【解析】
CD 对于A选项,y=f=sin=≠1,所以y=sin|x|的图象不关于x=对称,故A错误;对于B选项,y=cos|x|=cos
x,由余弦函数的图象可知,x=不是其对称轴,故B错误;对于C选项,函数y=|sin
2x|的周期为T=,y=f==1,由其函数图象知,x=是其对称轴,故C正确;对于D选项,函数y=|cos
2x|的周期为T=,y=f==0,由其函数图象知,x=是其对称轴,故D正确.故选CD.
11.
【解析】AC 因为y=log4x在(0,+∞)上单调递增,且0
12.
【解析】 AB 把x=π代入,f(x)=3sin=3sinπ=-3,取得最小值,所以x=π为对称轴,A正确;令2kπ-≤2x-≤2kπ+(k∈Z),解得kπ-≤kπ+(k∈Z),当k=0时,增区间为,B正确;y=3sin
2x的图象向右平移个单位长度可以得到图象C:y=3sin=3sin,所以C错误,把代入,f(x)=3sin=3sin≠0,y的值不为0,所以D错误.故选AB.
三、填空题:本题共4小题,每小题5分,共20分.
13.【解析】2 设扇形的圆心角大小为α(rad),半径为r.由题意可得,扇形的面积S=αr2,即4=×2×r2,解得r=2.
14.
【解析】
f(x)= 4 设函数f(x)=xm,则f(3)=3m=?m=,所以f(x)=x=.f(a)==2?a=4.
15.
【解析】3+2 由题意可知,令x+3=1,则y=-1,即x=-2,y=-1,所以A(-2,-1),可得2m+n=1,所以+==3++≥3+2,当且仅当,即时,等号成立,所以+的最小值为3+2.
16.【解析】- cos-sin2=cos-sin2=-cos-sin2=-cos+cos2-1=-+-1=-.
四、解答题:本题共6个小题,共70分.
解答应写出文字说明、证明过程或演算步骤.
17.
.
【详解】
(1)因为,所以为第三象限或第四象限角;
若选③,;
若选④,;
(2)原式.
18.
【详解】
(1)
f(x)=lg(x-1)的定义域为(1,+∞),g(x)=lg(4-x)的定义域为(-∞,4),所以函数h(x)=f(x)-g(x)的定义域为(1,4).
(2)
不等式f(x)>g(x),等价于lg(x-1)>lg(4-x),即x-1>4-x,解得x>.
又定义域为(1,4),所以实数x的取值范围为.
19.
【详解】
(1)
由已知条件及三角函数的定义可知,cos
α=,cos
β=,因为α为锐角,故sin
α>0,从而sin
α==;因为β为锐角,故sin
β>0,从而sin
β==.
(2)
==-=-=-.
20.
【详解】
(1)
因为f(x)定义在R上的奇函数,所以f(0)=0,得a=-2.此时f(x)=1-=,f(-x)===-f(x),所以f(x)是奇函数,所以a=-2.任取x1,x2∈R,且x1
因为f(x)为奇函数,f(t2-2t)+f(2t2-k)<0的解集非空,所以f(t2-2t)
21.
(1)
由图可知,A=2,=-=,则T=π,所以ω=2,由2×+φ=+2kπ,|φ|<π,得φ=-,所以f(x)=2sin.
(2)
将函数f(x)图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得y=2sin,再将得到的图象向左平移个单位长度,得到函数g(x)=2sin,令-+2kπ≤x+≤+2kπ,解得-+2kπ≤x≤+2kπ,k∈Z.取k=0,可得-≤x≤,所以函数y=g(x)在x∈上的单调递增区间为.
22.
【详解】
设调出人参加项目从事售后服务工作
(1)由题意得:,
即,又,所以.即最多调整500名员工从事第三产业.
(2)由题知,,
从事第三产业的员工创造的年总利润为万元,
从事原来产业的员工的年总利润为万元,
则,
所以,
所以,即恒成立,
因为,所以,所以,
又,所以,即的取值范围为.
同课章节目录
