【同步提优常题专训】7.2 坐标方法的简单应用(含解析)
文档属性
| 名称 | 【同步提优常题专训】7.2 坐标方法的简单应用(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 891.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 14:36:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教版七年级数学下册同步提优常考题专训
第七章
平面直角坐标系
7.2
坐标方法的简单应用
一.选择题
1.(2019秋?五华区期末)在平面直角坐标系xOy中,以原点O为圆心,任意长为半径作弧,分别交x轴的负半轴和y轴的正半轴于A点,B点,分别以点A,点B为圆心,AB的长为半径作弧,两弧交于P点,若点P的坐标为(m,n),则下列结论正确的是( )
A.m=2n
B.2m=n
C.m=n
D.m=﹣n
2.(2020秋?西华县期中)如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1)
B.(1,3)
C.(3,1)
D.(3,﹣1)
3.(2020春?江夏区月考)如图,若在象棋盘上建立平面直角坐标系,使棋子“车”的坐标为(﹣2,2),“马”的坐标为(1,2),则棋子“炮”的坐标为( )
A.(3,2)
B.(3,1)
C.(2,2)
D.(﹣2,2)
4.(2020秋?濉溪县期中)将点A(﹣4,﹣1)先向右平移5个单位,再向上平移3个单位得到点A1,则点A1的坐标为( )
A.(1,2)
B.(2,9)
C.(5,3)
D.(﹣9,﹣4)
5.(2020秋?武侯区校级期中)在平面直角坐标系中,将点A(x,y)向左平移3个单位长度,再向上平移5个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5)
B.(0,﹣3)
C.(﹣2,5)
D.(5,﹣3)
6.(2020秋?丰台区期中)如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4)
B.(5,4)
C.(7,0)
D.(8,1)
7.(2019秋?包河区期末)如图,在平面直角坐标系中,A(﹣3,0),B(3,0),C(3,4),点P为任意一点,已知PA⊥PB,则线段PC的最大值为( )
A.3
B.5
C.8
D.10
8.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( )
A.a可取任意实数,b=5
B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5
D.a=﹣1,b≠5
二.填空题
9.(2020秋?道里区期末)已知点A(3,2),将点A先向左平移4个单位长度,再向上平移5个单位长度得到点B,则B的坐标为
.
10.(2020秋?朝阳区校级月考)如图,点A、B的坐标分别为(0,2)、(3,0).若将线段AB平移至A1B1,则a2+b2的值为
.
11.(2020秋?即墨区校级期中)如图所示的棋盘放置在某个平面直角坐标系内,棋子①的坐标为(﹣1,﹣2),棋子②的坐标为(2,﹣3),那么棋子③的坐标是
.
12.(2020秋?武侯区校级期中)已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移2个单位长度后的坐标为
.
13.(2020?柳州)点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为
.
14.(2020秋?包河区校级月考)如果将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点B,那么点B在第
象限,点B的坐标是
.
15.(2020春?无棣县期末)如图,若在象棋盘上建立平面直角坐标系,使棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为
.
16.(2020春?临颍县期末)如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为
.
17.(2020秋?成都期中)已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移3个单位长度后的坐标为
.
三.解答题
18.(2020秋?松北区期末)按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为
;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为
.
19.(2020秋?叶县期中)(1)已知点P(2x+3,4x﹣7)的横坐标减纵坐标的差为6,求这个点到x轴、y轴的距离;
(2)已知点A(2x﹣3,6﹣x)到两坐标轴的距离相等,且在第二象限,求点A的坐标;
(3)已知线段AB平行于y轴,点A的坐标为(﹣2,3),且AB=4,求点B的坐标.
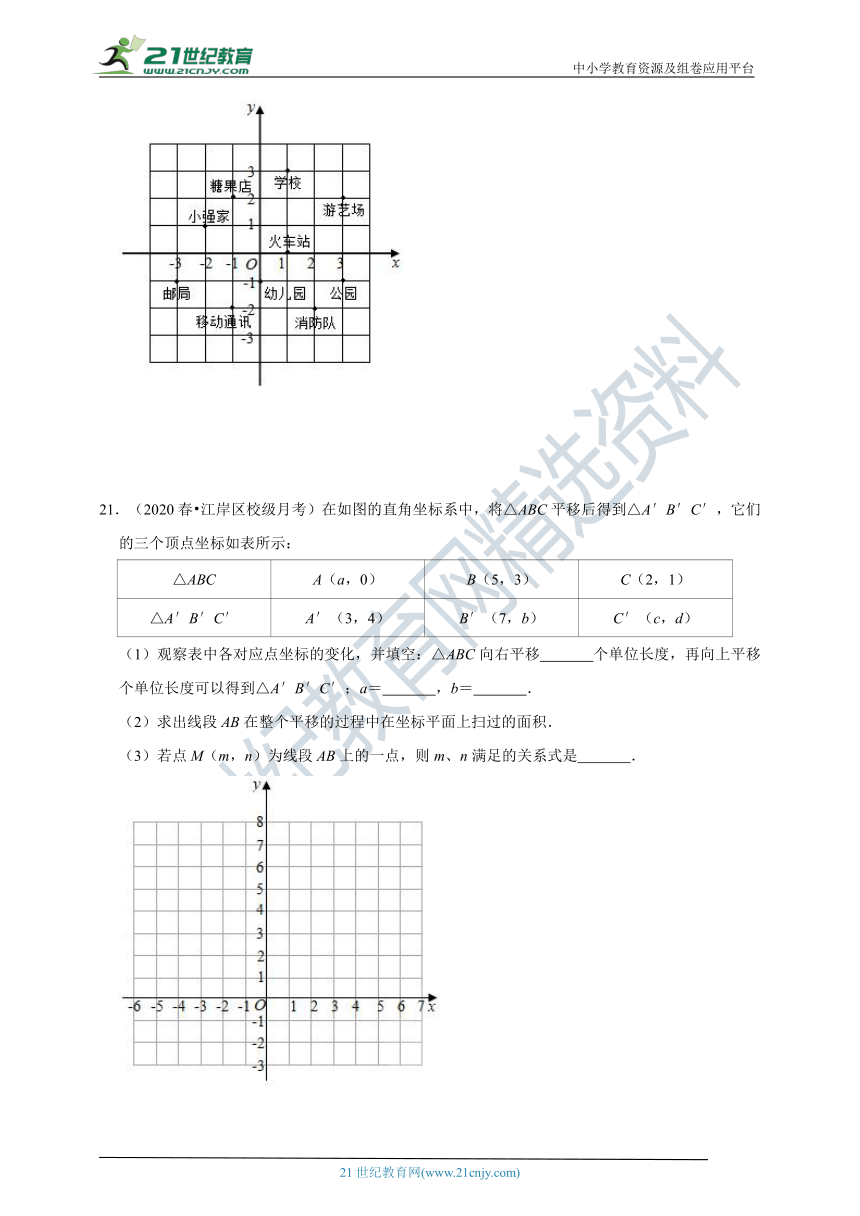
20.(2020秋?龙岗区校级期中)图中标明了小强家附近的一些地方.
(1)写出公园、游艺场和学校的坐标;
(2)早晨,小强从家里出发,沿(﹣3,﹣1),(﹣1,﹣2),(0,﹣1),(2,﹣2),(1,0),(1,3),(﹣1,2)路线转了一下,又回到家里,写出他路上经过的地方.
21.(2020春?江岸区校级月考)在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的三个顶点坐标如表所示:
△ABC
A(a,0)
B(5,3)
C(2,1)
△A′B′C′
A′(3,4)
B′(7,b)
C′(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向右平移
个单位长度,再向上平移
个单位长度可以得到△A′B′C′;a=
,b=
.
(2)求出线段AB在整个平移的过程中在坐标平面上扫过的面积.
(3)若点M(m,n)为线段AB上的一点,则m、n满足的关系式是
.
22.(2020秋?大新县期中)已知平面直角坐标系中有一点M(2m﹣3,m+1).
(1)点N(5,﹣1)且MN∥x轴时,求点M的坐标;
(2)若点M到y轴的距离为2时,求点M的坐标.
23.(2020春?西乡塘区校级月考)已知点A(a﹣1,﹣2),B(﹣3,b+1),根据以下要求确定a,b的值.
(1)当直线AB∥x轴时,a
,b
;
(2)当直线AB∥y轴时,a
,b
;
(3)当点A和点B在二四象限的角平分线上时,求a,b的值.
24.(2020春?西华县期中)如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标(
,
).
25.(2020春?西华县期中)已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.
(1)点P在y轴上;
(2)点P到x轴、y轴的距离相等,且点P在第二象限;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
26.(2020春?东湖区期末)△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A
; B
;C
;
(2)△ABC由△A′B′C′经过怎样的平移得到?答:
.
(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为
;
(4)求△ABC的面积.
27.(2019春?德州期中)已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
28.(2019春?江城区期中)如图,三角形ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度得到三角形EFG.
(1)写出三角形EFG的三个顶点坐标;
(2)求三角形EFG的面积.
参考答案与试题解析
一.选择题
1.【解答】解:如图,m,n的数量关系为m+n=0.
故选:D.
2.【解答】解:∵点A(﹣3,3)绕原点O旋转180°到乙位置,
∴A在乙位置时的坐标为(3,﹣3),
∵A在乙位置再将它向上平移2个单位长到丙位置,
∴丙位置中的对应点A′的坐标为(3,﹣1).
故选:D.
3.【解答】解:如图所示:
棋子“炮”的坐标为(3,1).
故选:B.
4.【解答】解:∵把点A(﹣4,﹣1)先向右平移5个单位长度,故得到:(1,﹣1);
再向上平移3个单位长度得到点A′(1,2).
故选:A.
5.【解答】解:∵点A(x,y)向左平移3个单位长度,再向上平移5个单位长度后与点B(﹣3,2)重合,
∴x﹣3=﹣3,y+5=2,
解得x=0,y=﹣3,
所以,点A的坐标是(0,﹣3).
故选:B.
6.【解答】解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
7.【解答】解:如图所示,连接OC,OP,PC,
∵PA⊥PB,
∴∠APB=90°,
又∵AO=BO=3,
∴Rt△ABP中,OPAB=3,
∵OC﹣OP≤CP≤OP+OC,
∴当点P,O,C在同一直线上,且点P在CO延长线上时,CP的最大值为OP+OC的长,
∴线段PC的最大值为OP+OC=3+5=8,
故选:C.
8.【解答】解:∵AB∥x轴,
∴b=5,a≠﹣1,
故选:C.
二.填空题
9.【解答】解:由点A(3,2),根据平移的性质可知:
将点A先向左平移4个单位长度,再向上平移5个单位长度得到点B,
则B的坐标为(﹣1,7).
故答案为:(﹣1,7).
10.【解答】解:因为A、B两点的坐标分别为(0,2)、(3,0),
将线段AB平移至A1B1,
点A1,B1的坐标分别为(a,3)、(5,b),
∴3﹣2=1,5﹣3=2,
说明线段AB向右移动2个单位,向上平移1个单位,
∴a=2,b=1,
则a2+b2=22+12=5.
故答案为:5.
11.【解答】解:如图所示:棋子③的坐标是(3,﹣1).
故答案为:(3,﹣1).
12.【解答】解:∵A(a﹣5,2b﹣1)在y轴上,
∴a﹣5=0,
解得:a=5,
∵B(3a+2,b+3)在x轴上,
∴b+3=0,
解得:b=﹣3,
∴C点坐标为(5,﹣3),
∵C向左平移2个单位长度再向上平移2个单位长度,
∴所的对应点坐标为(5﹣2,﹣3+2),
即(3,﹣1),
故答案为:(3,﹣1).
13.【解答】解:将点A(2,﹣3)向上平移4个单位得到点A′,
则点A′的坐标是(2,﹣3+4),即(2,1).
故答案为(2,1).
14.【解答】解:将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点B,那么点B的坐标是(﹣3+2,﹣2+3),即(﹣1,1).
∴点B在第二象限,
故答案为二,(﹣1,1).
15.【解答】解:如图所示:棋子“炮”的坐标为(3,2).
故答案是:(3,2).
16.【解答】解:如图,设P点坐标为(x,0),
根据题意得?4?|6﹣x|=6,
解得x=3或9,
所以P点坐标为(3,0)或(9,0).
故答案为:(3,0)或(9,0).
17.【解答】解:∵A(a﹣5,2b﹣1)在y轴上,
∴a﹣5=0,
解得:a=5,
∵B(3a+2,b+3)在x轴上,
∴b+3=0,
解得:b=﹣3,
∴C点坐标为(5,﹣3),
∵C向左平移2个单位长度再向上平移3个单位长度,
∴所的对应点坐标为(5﹣2,﹣3+3),
即(3,0),
故答案为:(3,0).
三.解答题
18.【解答】解:(1)如图所示:点A的坐标为(﹣4,2);
故答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×41×32×31×4=5.5.
故答案为:5.5.
19.【解答】解:(1)根据题意得,(2x+3)﹣(4x﹣7)=6,
解得,x=2,
∴P(7,1),
∴这个点到x轴的距离是1,到y轴的距离是7;
(2)∵A(2x﹣3,6﹣x)在第二象限,
∴2x﹣3<0,6﹣x>0,
根据题意得,﹣(2x﹣3)=6﹣x,
解得,x=﹣3,
∴A(﹣9,9);
(3)∵线段AB平行于y轴,点A的坐标为(﹣2,3),
∴点B点的横坐标是﹣2,
又∵AB=4,
∴当B点在A点上方时,B点的纵坐标是3+4=7,
当B点在A点下方时,B点的纵坐标是3﹣4=﹣1,
∴B点坐标是(﹣2,7)或(﹣2,﹣1).
20.【解答】解:(1)公园(3,﹣1),游艺场(3,2),学校(1,3);
(2)邮局﹣﹣移动通讯﹣﹣幼儿园﹣﹣消防队﹣﹣火车站﹣﹣学校﹣﹣糖果店.
21.【解答】解:(1)∵A(a,0),A′(3,4),
∴△ABC向上平移4个单位后得到△A′B′C′,
∵B(5,3),B′(7,b),
∴△ABC向右平移2个单位后得到△A′B′C′,
∴a=1,b=3+4=7,
故答案为:2;4;1;7;
(2)线段AB在整个平移的过程中在坐标平面上扫过的面积:2×3+4×4=22;
(3)设AB所在直线解析式为y=kx+b,
∵A(1,0),B(5,3),
∴,
解得:,
∴AB所在直线解析式为yx,
∵点M(m,n)为线段AB上的一点,
∴nm,
即:3m﹣4n=3,
故答案为:3m﹣4n=3.
22.【解答】解:(1)∵点M(2m﹣3,m+1),点N(5,﹣1)且MN∥x轴,
∴m+1=﹣1,
解得m=﹣2,
故点M的坐标为(﹣7,﹣1).
(2)∵点M(2m﹣3,m+1),点M到y轴的距离为2,
∴|2m﹣3|=2,
解得m=2.5或m=0.5,
当m=2.5时,点M的坐标为(2,3.5);
当m=0.5时,点M的坐标为(﹣2,1.5);
综上所述,点M的坐标为(2,3.5)或(﹣2,1.5).
23.【解答】解:(1)∵直线AB∥x轴,
∴点A与点B的纵坐标相同,
∴b+1=﹣2,
∴b=﹣3,
∵AB是直线,
∴A,B不重合,
∴a﹣1≠﹣3,
解得:a≠﹣2,
故答案是:≠﹣2,=﹣3;
(2)∵直线AB∥y轴,
∴点A与点B的横坐标相同,A,B点纵坐标不相等,
∴a﹣1=﹣3,﹣2≠b+1,
∴a=﹣2,b≠﹣3;
故答案是:=﹣2,≠﹣3;
(3)∵A、B两点在第二、四象限的角平分线上,
∴a﹣1+(﹣2)=0,b+1+(﹣3)=0,
∴a=3,b=2.
24.【解答】解:(1)如图,△ABC即为所求.
S△ABC=4×52×42×52×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
25.【解答】解:(1)∵点P(2x﹣6,3x+1),且点P在y轴上,
∴2x﹣6=0,
∴x=3,
∴3x+1=10,
∴点P的坐标为(0,10);
(2)∵点P(2x﹣6,3x+1),点P到x轴、y轴的距离相等,且点P在第二象限,
∴2x﹣6=﹣(3x+1),
∴2x﹣6+3x+1=0,
∴x=1,
∴2x﹣6=﹣4,3x+1=4,
∴点P的坐标为(﹣4,4);
(3)∵点P(2x﹣6,3x+1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2x﹣6=2,
∴x=4,
∴3x+1=13,
∴点P的坐标为(2,13).
26.【解答】解:(1)A(1,3);
B(2,0);C(3,1);
(2)先向右平移4个单位,再向上平移2个单位;
或:先向上平移2个单位,再向右平移4个单位;
(3)P′(x﹣4,y﹣2);
(4)△ABC的面积=2×31×31×12×2
=6﹣1.5﹣0.5﹣2
=2.
故答案为:(1)(1,3);
(2,0);(3,1);(2)先向右平移4个单位,再向上平移2个单位;(3)(x﹣4,y﹣2).
27.【解答】解:(1)∵点M在x轴上,
∴a﹣1=0,
∴a=1,
3a﹣8=3﹣8=﹣5,a﹣1=0,
∴点M的坐标是(﹣5,0);
(2)∵点M在第二、四象限的角平分线上,
∴3a﹣8+a﹣1=0,
解得a,
∴a﹣11,
∴点M的坐标为(,);
(3)∵直线MN∥y轴,
∴3a﹣8=1,
解得a=3,
∴a﹣1=3﹣1=2,
点M(1,2).
28.【解答】解:(1)如图:
E(4,1),F(0,﹣2),G(5,﹣3).
(2)S△EFG=4×5﹣3×41×54×120﹣6﹣2.5﹣2=9.5.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教版七年级数学下册同步提优常考题专训
第七章
平面直角坐标系
7.2
坐标方法的简单应用
一.选择题
1.(2019秋?五华区期末)在平面直角坐标系xOy中,以原点O为圆心,任意长为半径作弧,分别交x轴的负半轴和y轴的正半轴于A点,B点,分别以点A,点B为圆心,AB的长为半径作弧,两弧交于P点,若点P的坐标为(m,n),则下列结论正确的是( )
A.m=2n
B.2m=n
C.m=n
D.m=﹣n
2.(2020秋?西华县期中)如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1)
B.(1,3)
C.(3,1)
D.(3,﹣1)
3.(2020春?江夏区月考)如图,若在象棋盘上建立平面直角坐标系,使棋子“车”的坐标为(﹣2,2),“马”的坐标为(1,2),则棋子“炮”的坐标为( )
A.(3,2)
B.(3,1)
C.(2,2)
D.(﹣2,2)
4.(2020秋?濉溪县期中)将点A(﹣4,﹣1)先向右平移5个单位,再向上平移3个单位得到点A1,则点A1的坐标为( )
A.(1,2)
B.(2,9)
C.(5,3)
D.(﹣9,﹣4)
5.(2020秋?武侯区校级期中)在平面直角坐标系中,将点A(x,y)向左平移3个单位长度,再向上平移5个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5)
B.(0,﹣3)
C.(﹣2,5)
D.(5,﹣3)
6.(2020秋?丰台区期中)如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4)
B.(5,4)
C.(7,0)
D.(8,1)
7.(2019秋?包河区期末)如图,在平面直角坐标系中,A(﹣3,0),B(3,0),C(3,4),点P为任意一点,已知PA⊥PB,则线段PC的最大值为( )
A.3
B.5
C.8
D.10
8.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( )
A.a可取任意实数,b=5
B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5
D.a=﹣1,b≠5
二.填空题
9.(2020秋?道里区期末)已知点A(3,2),将点A先向左平移4个单位长度,再向上平移5个单位长度得到点B,则B的坐标为
.
10.(2020秋?朝阳区校级月考)如图,点A、B的坐标分别为(0,2)、(3,0).若将线段AB平移至A1B1,则a2+b2的值为
.
11.(2020秋?即墨区校级期中)如图所示的棋盘放置在某个平面直角坐标系内,棋子①的坐标为(﹣1,﹣2),棋子②的坐标为(2,﹣3),那么棋子③的坐标是
.
12.(2020秋?武侯区校级期中)已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移2个单位长度后的坐标为
.
13.(2020?柳州)点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为
.
14.(2020秋?包河区校级月考)如果将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点B,那么点B在第
象限,点B的坐标是
.
15.(2020春?无棣县期末)如图,若在象棋盘上建立平面直角坐标系,使棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为
.
16.(2020春?临颍县期末)如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为
.
17.(2020秋?成都期中)已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)向左平移2个单位长度再向上平移3个单位长度后的坐标为
.
三.解答题
18.(2020秋?松北区期末)按要求画图及填空:
在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
(1)点A的坐标为
;
(2)将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1,画出△A1B1C1.
(3)△A1B1C1的面积为
.
19.(2020秋?叶县期中)(1)已知点P(2x+3,4x﹣7)的横坐标减纵坐标的差为6,求这个点到x轴、y轴的距离;
(2)已知点A(2x﹣3,6﹣x)到两坐标轴的距离相等,且在第二象限,求点A的坐标;
(3)已知线段AB平行于y轴,点A的坐标为(﹣2,3),且AB=4,求点B的坐标.
20.(2020秋?龙岗区校级期中)图中标明了小强家附近的一些地方.
(1)写出公园、游艺场和学校的坐标;
(2)早晨,小强从家里出发,沿(﹣3,﹣1),(﹣1,﹣2),(0,﹣1),(2,﹣2),(1,0),(1,3),(﹣1,2)路线转了一下,又回到家里,写出他路上经过的地方.
21.(2020春?江岸区校级月考)在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的三个顶点坐标如表所示:
△ABC
A(a,0)
B(5,3)
C(2,1)
△A′B′C′
A′(3,4)
B′(7,b)
C′(c,d)
(1)观察表中各对应点坐标的变化,并填空:△ABC向右平移
个单位长度,再向上平移
个单位长度可以得到△A′B′C′;a=
,b=
.
(2)求出线段AB在整个平移的过程中在坐标平面上扫过的面积.
(3)若点M(m,n)为线段AB上的一点,则m、n满足的关系式是
.
22.(2020秋?大新县期中)已知平面直角坐标系中有一点M(2m﹣3,m+1).
(1)点N(5,﹣1)且MN∥x轴时,求点M的坐标;
(2)若点M到y轴的距离为2时,求点M的坐标.
23.(2020春?西乡塘区校级月考)已知点A(a﹣1,﹣2),B(﹣3,b+1),根据以下要求确定a,b的值.
(1)当直线AB∥x轴时,a
,b
;
(2)当直线AB∥y轴时,a
,b
;
(3)当点A和点B在二四象限的角平分线上时,求a,b的值.
24.(2020春?西华县期中)如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标(
,
).
25.(2020春?西华县期中)已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.
(1)点P在y轴上;
(2)点P到x轴、y轴的距离相等,且点P在第二象限;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
26.(2020春?东湖区期末)△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A
; B
;C
;
(2)△ABC由△A′B′C′经过怎样的平移得到?答:
.
(3)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为
;
(4)求△ABC的面积.
27.(2019春?德州期中)已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
28.(2019春?江城区期中)如图,三角形ABC沿x轴正方向平移2个单位长度,再沿y轴负方向平移1个单位长度得到三角形EFG.
(1)写出三角形EFG的三个顶点坐标;
(2)求三角形EFG的面积.
参考答案与试题解析
一.选择题
1.【解答】解:如图,m,n的数量关系为m+n=0.
故选:D.
2.【解答】解:∵点A(﹣3,3)绕原点O旋转180°到乙位置,
∴A在乙位置时的坐标为(3,﹣3),
∵A在乙位置再将它向上平移2个单位长到丙位置,
∴丙位置中的对应点A′的坐标为(3,﹣1).
故选:D.
3.【解答】解:如图所示:
棋子“炮”的坐标为(3,1).
故选:B.
4.【解答】解:∵把点A(﹣4,﹣1)先向右平移5个单位长度,故得到:(1,﹣1);
再向上平移3个单位长度得到点A′(1,2).
故选:A.
5.【解答】解:∵点A(x,y)向左平移3个单位长度,再向上平移5个单位长度后与点B(﹣3,2)重合,
∴x﹣3=﹣3,y+5=2,
解得x=0,y=﹣3,
所以,点A的坐标是(0,﹣3).
故选:B.
6.【解答】解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
7.【解答】解:如图所示,连接OC,OP,PC,
∵PA⊥PB,
∴∠APB=90°,
又∵AO=BO=3,
∴Rt△ABP中,OPAB=3,
∵OC﹣OP≤CP≤OP+OC,
∴当点P,O,C在同一直线上,且点P在CO延长线上时,CP的最大值为OP+OC的长,
∴线段PC的最大值为OP+OC=3+5=8,
故选:C.
8.【解答】解:∵AB∥x轴,
∴b=5,a≠﹣1,
故选:C.
二.填空题
9.【解答】解:由点A(3,2),根据平移的性质可知:
将点A先向左平移4个单位长度,再向上平移5个单位长度得到点B,
则B的坐标为(﹣1,7).
故答案为:(﹣1,7).
10.【解答】解:因为A、B两点的坐标分别为(0,2)、(3,0),
将线段AB平移至A1B1,
点A1,B1的坐标分别为(a,3)、(5,b),
∴3﹣2=1,5﹣3=2,
说明线段AB向右移动2个单位,向上平移1个单位,
∴a=2,b=1,
则a2+b2=22+12=5.
故答案为:5.
11.【解答】解:如图所示:棋子③的坐标是(3,﹣1).
故答案为:(3,﹣1).
12.【解答】解:∵A(a﹣5,2b﹣1)在y轴上,
∴a﹣5=0,
解得:a=5,
∵B(3a+2,b+3)在x轴上,
∴b+3=0,
解得:b=﹣3,
∴C点坐标为(5,﹣3),
∵C向左平移2个单位长度再向上平移2个单位长度,
∴所的对应点坐标为(5﹣2,﹣3+2),
即(3,﹣1),
故答案为:(3,﹣1).
13.【解答】解:将点A(2,﹣3)向上平移4个单位得到点A′,
则点A′的坐标是(2,﹣3+4),即(2,1).
故答案为(2,1).
14.【解答】解:将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点B,那么点B的坐标是(﹣3+2,﹣2+3),即(﹣1,1).
∴点B在第二象限,
故答案为二,(﹣1,1).
15.【解答】解:如图所示:棋子“炮”的坐标为(3,2).
故答案是:(3,2).
16.【解答】解:如图,设P点坐标为(x,0),
根据题意得?4?|6﹣x|=6,
解得x=3或9,
所以P点坐标为(3,0)或(9,0).
故答案为:(3,0)或(9,0).
17.【解答】解:∵A(a﹣5,2b﹣1)在y轴上,
∴a﹣5=0,
解得:a=5,
∵B(3a+2,b+3)在x轴上,
∴b+3=0,
解得:b=﹣3,
∴C点坐标为(5,﹣3),
∵C向左平移2个单位长度再向上平移3个单位长度,
∴所的对应点坐标为(5﹣2,﹣3+3),
即(3,0),
故答案为:(3,0).
三.解答题
18.【解答】解:(1)如图所示:点A的坐标为(﹣4,2);
故答案为:(﹣4,2);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1B1C1的面积为:3×41×32×31×4=5.5.
故答案为:5.5.
19.【解答】解:(1)根据题意得,(2x+3)﹣(4x﹣7)=6,
解得,x=2,
∴P(7,1),
∴这个点到x轴的距离是1,到y轴的距离是7;
(2)∵A(2x﹣3,6﹣x)在第二象限,
∴2x﹣3<0,6﹣x>0,
根据题意得,﹣(2x﹣3)=6﹣x,
解得,x=﹣3,
∴A(﹣9,9);
(3)∵线段AB平行于y轴,点A的坐标为(﹣2,3),
∴点B点的横坐标是﹣2,
又∵AB=4,
∴当B点在A点上方时,B点的纵坐标是3+4=7,
当B点在A点下方时,B点的纵坐标是3﹣4=﹣1,
∴B点坐标是(﹣2,7)或(﹣2,﹣1).
20.【解答】解:(1)公园(3,﹣1),游艺场(3,2),学校(1,3);
(2)邮局﹣﹣移动通讯﹣﹣幼儿园﹣﹣消防队﹣﹣火车站﹣﹣学校﹣﹣糖果店.
21.【解答】解:(1)∵A(a,0),A′(3,4),
∴△ABC向上平移4个单位后得到△A′B′C′,
∵B(5,3),B′(7,b),
∴△ABC向右平移2个单位后得到△A′B′C′,
∴a=1,b=3+4=7,
故答案为:2;4;1;7;
(2)线段AB在整个平移的过程中在坐标平面上扫过的面积:2×3+4×4=22;
(3)设AB所在直线解析式为y=kx+b,
∵A(1,0),B(5,3),
∴,
解得:,
∴AB所在直线解析式为yx,
∵点M(m,n)为线段AB上的一点,
∴nm,
即:3m﹣4n=3,
故答案为:3m﹣4n=3.
22.【解答】解:(1)∵点M(2m﹣3,m+1),点N(5,﹣1)且MN∥x轴,
∴m+1=﹣1,
解得m=﹣2,
故点M的坐标为(﹣7,﹣1).
(2)∵点M(2m﹣3,m+1),点M到y轴的距离为2,
∴|2m﹣3|=2,
解得m=2.5或m=0.5,
当m=2.5时,点M的坐标为(2,3.5);
当m=0.5时,点M的坐标为(﹣2,1.5);
综上所述,点M的坐标为(2,3.5)或(﹣2,1.5).
23.【解答】解:(1)∵直线AB∥x轴,
∴点A与点B的纵坐标相同,
∴b+1=﹣2,
∴b=﹣3,
∵AB是直线,
∴A,B不重合,
∴a﹣1≠﹣3,
解得:a≠﹣2,
故答案是:≠﹣2,=﹣3;
(2)∵直线AB∥y轴,
∴点A与点B的横坐标相同,A,B点纵坐标不相等,
∴a﹣1=﹣3,﹣2≠b+1,
∴a=﹣2,b≠﹣3;
故答案是:=﹣2,≠﹣3;
(3)∵A、B两点在第二、四象限的角平分线上,
∴a﹣1+(﹣2)=0,b+1+(﹣3)=0,
∴a=3,b=2.
24.【解答】解:(1)如图,△ABC即为所求.
S△ABC=4×52×42×52×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
25.【解答】解:(1)∵点P(2x﹣6,3x+1),且点P在y轴上,
∴2x﹣6=0,
∴x=3,
∴3x+1=10,
∴点P的坐标为(0,10);
(2)∵点P(2x﹣6,3x+1),点P到x轴、y轴的距离相等,且点P在第二象限,
∴2x﹣6=﹣(3x+1),
∴2x﹣6+3x+1=0,
∴x=1,
∴2x﹣6=﹣4,3x+1=4,
∴点P的坐标为(﹣4,4);
(3)∵点P(2x﹣6,3x+1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2x﹣6=2,
∴x=4,
∴3x+1=13,
∴点P的坐标为(2,13).
26.【解答】解:(1)A(1,3);
B(2,0);C(3,1);
(2)先向右平移4个单位,再向上平移2个单位;
或:先向上平移2个单位,再向右平移4个单位;
(3)P′(x﹣4,y﹣2);
(4)△ABC的面积=2×31×31×12×2
=6﹣1.5﹣0.5﹣2
=2.
故答案为:(1)(1,3);
(2,0);(3,1);(2)先向右平移4个单位,再向上平移2个单位;(3)(x﹣4,y﹣2).
27.【解答】解:(1)∵点M在x轴上,
∴a﹣1=0,
∴a=1,
3a﹣8=3﹣8=﹣5,a﹣1=0,
∴点M的坐标是(﹣5,0);
(2)∵点M在第二、四象限的角平分线上,
∴3a﹣8+a﹣1=0,
解得a,
∴a﹣11,
∴点M的坐标为(,);
(3)∵直线MN∥y轴,
∴3a﹣8=1,
解得a=3,
∴a﹣1=3﹣1=2,
点M(1,2).
28.【解答】解:(1)如图:
E(4,1),F(0,﹣2),G(5,﹣3).
(2)S△EFG=4×5﹣3×41×54×120﹣6﹣2.5﹣2=9.5.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
