人教版九年级数学下册26.1.2反比例函数图像和性质课件(共25张PPT)
文档属性
| 名称 | 人教版九年级数学下册26.1.2反比例函数图像和性质课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 17:13:28 | ||
图片预览



文档简介
(共25张PPT)
正比例函数的图象和性质
位置
图象经过一、三象限
y随x的增大而增大
图象经过二、四象限
y随x的增大而减小
K>0
K<0
y=kx
(k≠0)
过原点的一条直线
增减性
图象
解析式
K>0
K<0
反比例函数的图象与性质
数缺形时少直觉,形少数时难入微.
活动一
画反比例函数
与
的图象。
画函数图象的步骤:
1、列表
2、描点
3、连线
x
…
…
…
…
应注意:
1、自变量x≠0;
2、自变量x的取值要对称
3、自变量x的取值要便于计算和描点
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
0
1
1
2
2
3
3
4
4
5
6
5
6
7
-1
-1
-2
-2
-3
-4
-4
-3
-5
-5
-6
-6
x
y
0
1
1
2
2
3
3
4
4
5
6
5
6
7
-1
-1
-2
-2
-3
-4
-4
-3
-5
-5
-6
-6
x
y
0
1
1
2
2
3
3
4
4
5
6
5
6
7
-1
-1
-2
-2
-3
-4
-4
-3
-5
-5
-6
-6
x
y
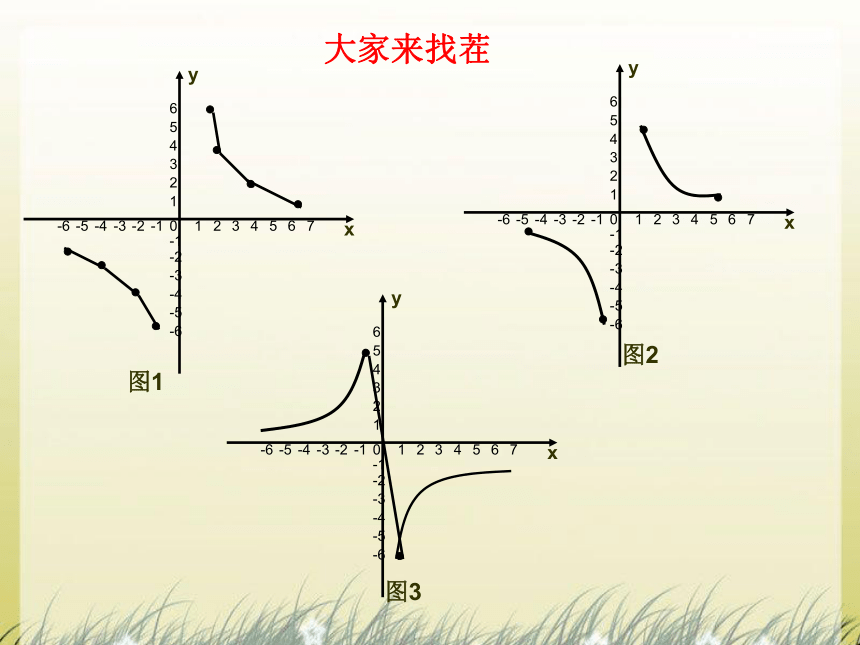
图1
图3
图2
大家来找茬
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y
=
x
6
y
=
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y
=
x
6
y
=-
x
6
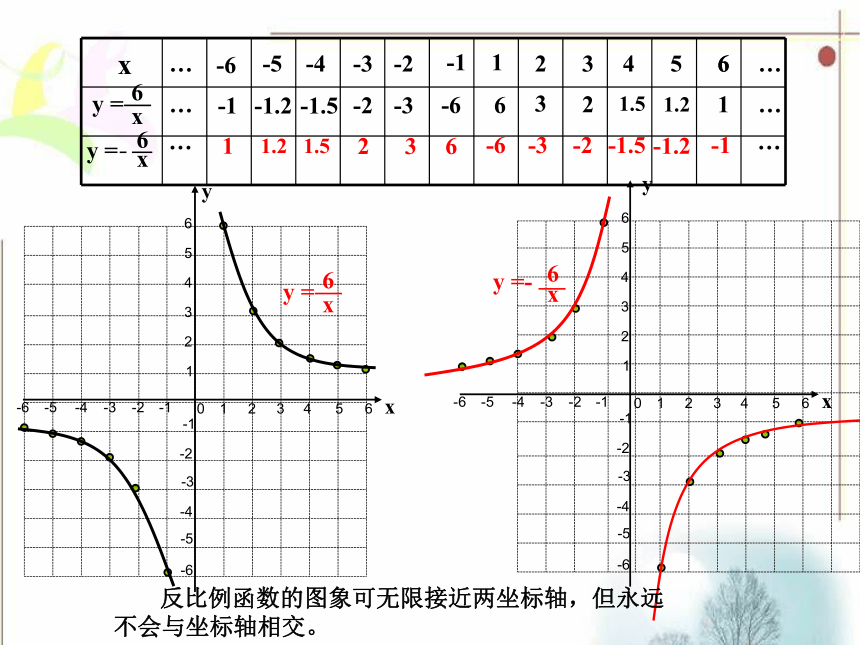
反比例函数的图象可无限接近两坐标轴,但永远不会与坐标轴相交。
仔细看一看
认真想一想
0
x
y
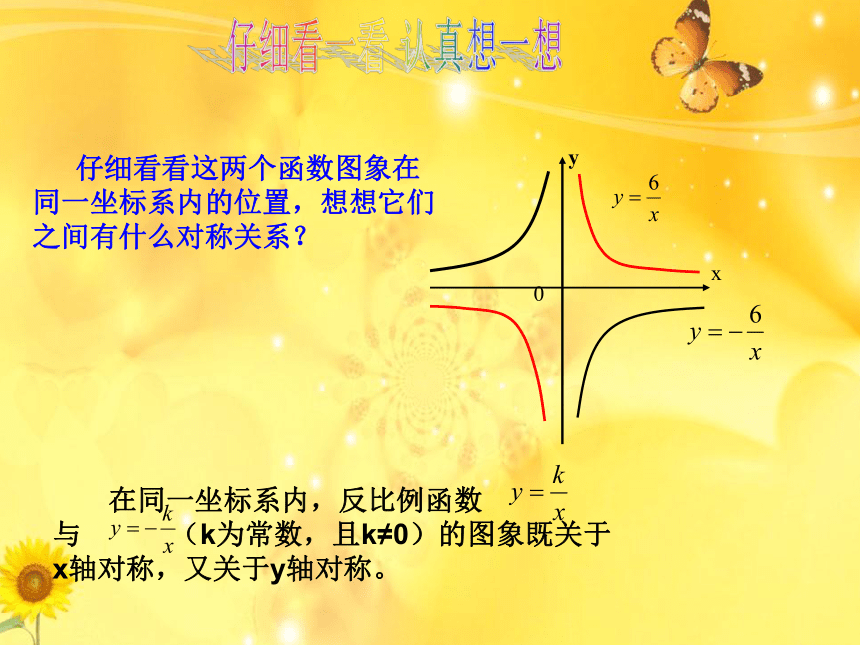
在同一坐标系内,反比例函数
与
(k为常数,且k≠0)的图象既关于x轴对称,又关于y轴对称。
仔细看看这两个函数图象在同一坐标系内的位置,想想它们之间有什么对称关系?
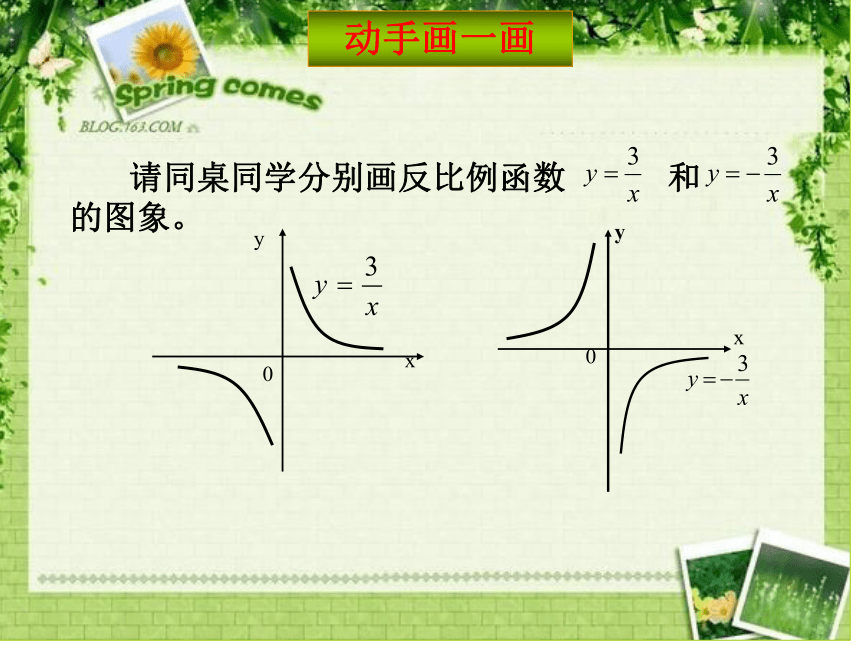
请同桌同学分别画反比例函数
和
的图象。
0
x
y
0
x
y
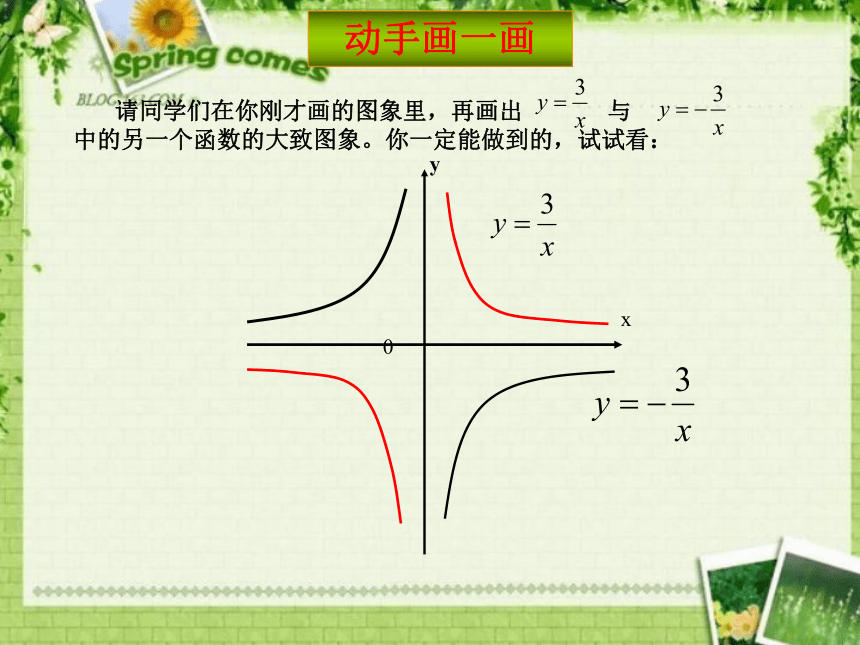
动手画一画
动手画一画
请同学们在你刚才画的图象里,再画出
与
中的另一个函数的大致图象。你一定能做到的,试试看:
0
x
y
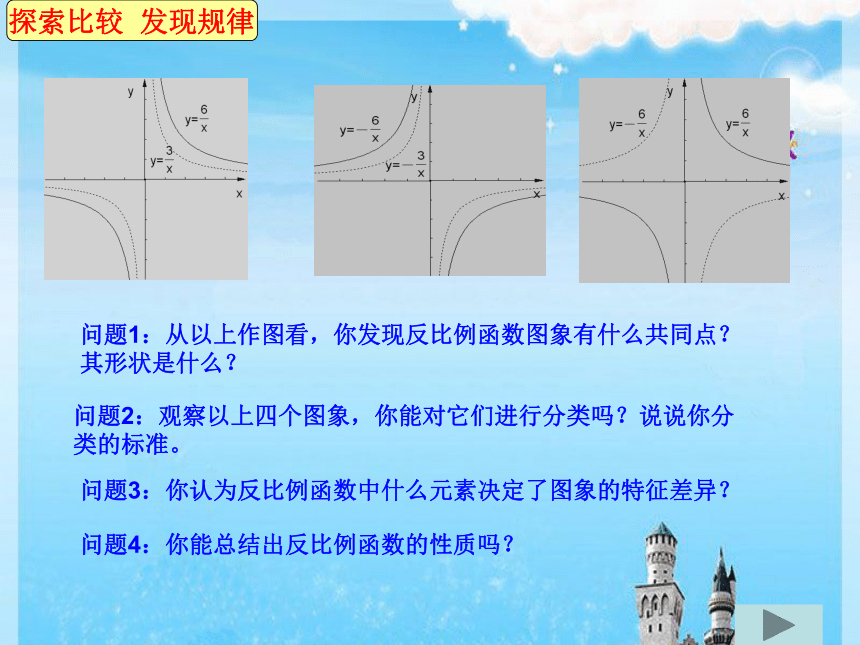
探索比较
发现规律
问题1:从以上作图看,你发现反比例函数图象有什么共同点?
其形状是什么?
问题2:观察以上四个图象,你能对它们进行分类吗?说说你分
类的标准。
问题3:你认为反比例函数中什么元素决定了图象的特征差异?
问题4:你能总结出反比例函数的性质吗?
A
XA
B
XB
函数值y怎样随着自变量x的变化而变化?
?
如xB<
xA
但yB<
yA
强调:在每一个象限内
由两支曲线组成的.
因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
反比例函数
与
的图象关于x轴对称,也关于y轴对称。
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
O
k>0
K<0
活动四
活动四
1、你问我答:请一位同学构造一个反比例函数,同桌指出
反比例函数图象所在象限及增减性。
2、已知反比例函数
若函数的图象位于第一三象限,求k的取值范围。
(2)若在每一象限内,y随x增大而增大,求k的取值范围。
以练促思
小试身手
2
2
1
1
1
2
对于反比例函数
,依据下列条
件,判断k与0之间的大小关系:
(1)若其图象在第一、三象限内,则k
0;
(2)若每一个象限内,y随x的增大而增大,则k
0
>
<
A1
下列函数中,图象位于第二、四象限的有
;在图象所在象限内,y的值随x的增大而增大的有
.
(3)、(4)
(2)、(3)、(5)
A2
已知
k<0,
函数
y1=kx,
y2=
在同
一坐标系中的图象大致是
(
)
x
k
C
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
x
y
0
y
B1
?
函数y=kx+k
与
在同一条直角坐标系中的
图象可能是
:
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
A
B2
已知点A(-2,y1),B(-1,y2)都在反比例函数
的图象上,则y1与y2的大小关系(从大到小)为
.
y1>
y2
C1
已知点A(-2,y1),B(-1,y2)都在反比例函数
的图象上,则y1与y2的大小
关系(从大到小)为
.
(k<0)
y2>
y1
C2
已知点
A(-2,y1),B(-1,y2),C(4,y3)
都在反比例
函数
的图象上,则y1、y2与y3的大小关系
(从大到小)为
.
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3
>y1>y2
挑战自我
活动五
知识回顾
根据下表请同学们回顾本节课所学的知识。
函数
正比例函数
反比例函数
解析式
图象形状
k>0
位置
增减性
k<0
位置
增减性
y=kx
(
k≠0
)
直线
双曲线
一、三象限
一、三象限
y随x的增大而增大
每个象限内,y随x的增大而减小
每个象限内,y随x的增大而增大。
y随x的增大而减小
二、四象限
二、四象限
注意:
1、双曲线越来越接近两坐标轴,但永远不会与坐标轴相交。
2、在同一坐标系内,反比例函数
与
的图象既关于x轴对称,又关于y轴对称。
作业
课本46页第3题、47页第8题。
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
——老师与同学们共勉
正比例函数的图象和性质
位置
图象经过一、三象限
y随x的增大而增大
图象经过二、四象限
y随x的增大而减小
K>0
K<0
y=kx
(k≠0)
过原点的一条直线
增减性
图象
解析式
K>0
K<0
反比例函数的图象与性质
数缺形时少直觉,形少数时难入微.
活动一
画反比例函数
与
的图象。
画函数图象的步骤:
1、列表
2、描点
3、连线
x
…
…
…
…
应注意:
1、自变量x≠0;
2、自变量x的取值要对称
3、自变量x的取值要便于计算和描点
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
0
1
1
2
2
3
3
4
4
5
6
5
6
7
-1
-1
-2
-2
-3
-4
-4
-3
-5
-5
-6
-6
x
y
0
1
1
2
2
3
3
4
4
5
6
5
6
7
-1
-1
-2
-2
-3
-4
-4
-3
-5
-5
-6
-6
x
y
0
1
1
2
2
3
3
4
4
5
6
5
6
7
-1
-1
-2
-2
-3
-4
-4
-3
-5
-5
-6
-6
x
y
图1
图3
图2
大家来找茬
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y
=
x
6
y
=
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y
=
x
6
y
=-
x
6
反比例函数的图象可无限接近两坐标轴,但永远不会与坐标轴相交。
仔细看一看
认真想一想
0
x
y
在同一坐标系内,反比例函数
与
(k为常数,且k≠0)的图象既关于x轴对称,又关于y轴对称。
仔细看看这两个函数图象在同一坐标系内的位置,想想它们之间有什么对称关系?
请同桌同学分别画反比例函数
和
的图象。
0
x
y
0
x
y
动手画一画
动手画一画
请同学们在你刚才画的图象里,再画出
与
中的另一个函数的大致图象。你一定能做到的,试试看:
0
x
y
探索比较
发现规律
问题1:从以上作图看,你发现反比例函数图象有什么共同点?
其形状是什么?
问题2:观察以上四个图象,你能对它们进行分类吗?说说你分
类的标准。
问题3:你认为反比例函数中什么元素决定了图象的特征差异?
问题4:你能总结出反比例函数的性质吗?
A
XA
B
XB
函数值y怎样随着自变量x的变化而变化?
?
如xB<
xA
但yB<
yA
强调:在每一个象限内
由两支曲线组成的.
因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
反比例函数
与
的图象关于x轴对称,也关于y轴对称。
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
O
k>0
K<0
活动四
活动四
1、你问我答:请一位同学构造一个反比例函数,同桌指出
反比例函数图象所在象限及增减性。
2、已知反比例函数
若函数的图象位于第一三象限,求k的取值范围。
(2)若在每一象限内,y随x增大而增大,求k的取值范围。
以练促思
小试身手
2
2
1
1
1
2
对于反比例函数
,依据下列条
件,判断k与0之间的大小关系:
(1)若其图象在第一、三象限内,则k
0;
(2)若每一个象限内,y随x的增大而增大,则k
0
>
<
A1
下列函数中,图象位于第二、四象限的有
;在图象所在象限内,y的值随x的增大而增大的有
.
(3)、(4)
(2)、(3)、(5)
A2
已知
k<0,
函数
y1=kx,
y2=
在同
一坐标系中的图象大致是
(
)
x
k
C
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
x
y
0
y
B1
?
函数y=kx+k
与
在同一条直角坐标系中的
图象可能是
:
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
A
B2
已知点A(-2,y1),B(-1,y2)都在反比例函数
的图象上,则y1与y2的大小关系(从大到小)为
.
y1>
y2
C1
已知点A(-2,y1),B(-1,y2)都在反比例函数
的图象上,则y1与y2的大小
关系(从大到小)为
.
(k<0)
y2>
y1
C2
已知点
A(-2,y1),B(-1,y2),C(4,y3)
都在反比例
函数
的图象上,则y1、y2与y3的大小关系
(从大到小)为
.
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3
>y1>y2
挑战自我
活动五
知识回顾
根据下表请同学们回顾本节课所学的知识。
函数
正比例函数
反比例函数
解析式
图象形状
k>0
位置
增减性
k<0
位置
增减性
y=kx
(
k≠0
)
直线
双曲线
一、三象限
一、三象限
y随x的增大而增大
每个象限内,y随x的增大而减小
每个象限内,y随x的增大而增大。
y随x的增大而减小
二、四象限
二、四象限
注意:
1、双曲线越来越接近两坐标轴,但永远不会与坐标轴相交。
2、在同一坐标系内,反比例函数
与
的图象既关于x轴对称,又关于y轴对称。
作业
课本46页第3题、47页第8题。
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
——老师与同学们共勉
