六年级下册数学教案-3.1 用转化的策略解决问题 苏教版
文档属性
| 名称 | 六年级下册数学教案-3.1 用转化的策略解决问题 苏教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览

文档简介
用转化的策略解决问题
教学目标:
1.教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形.2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。3.进一步积累解决问题的经验,增强解决问题的"转化"意识,提高学好数学的信心.
教学重点: 感受“转化”策略的价值,会用“转化”的策略解决问题。
教学难点: 会用“转化”的策略解决问题。
教师准备:电子白板课件、白板互动平台
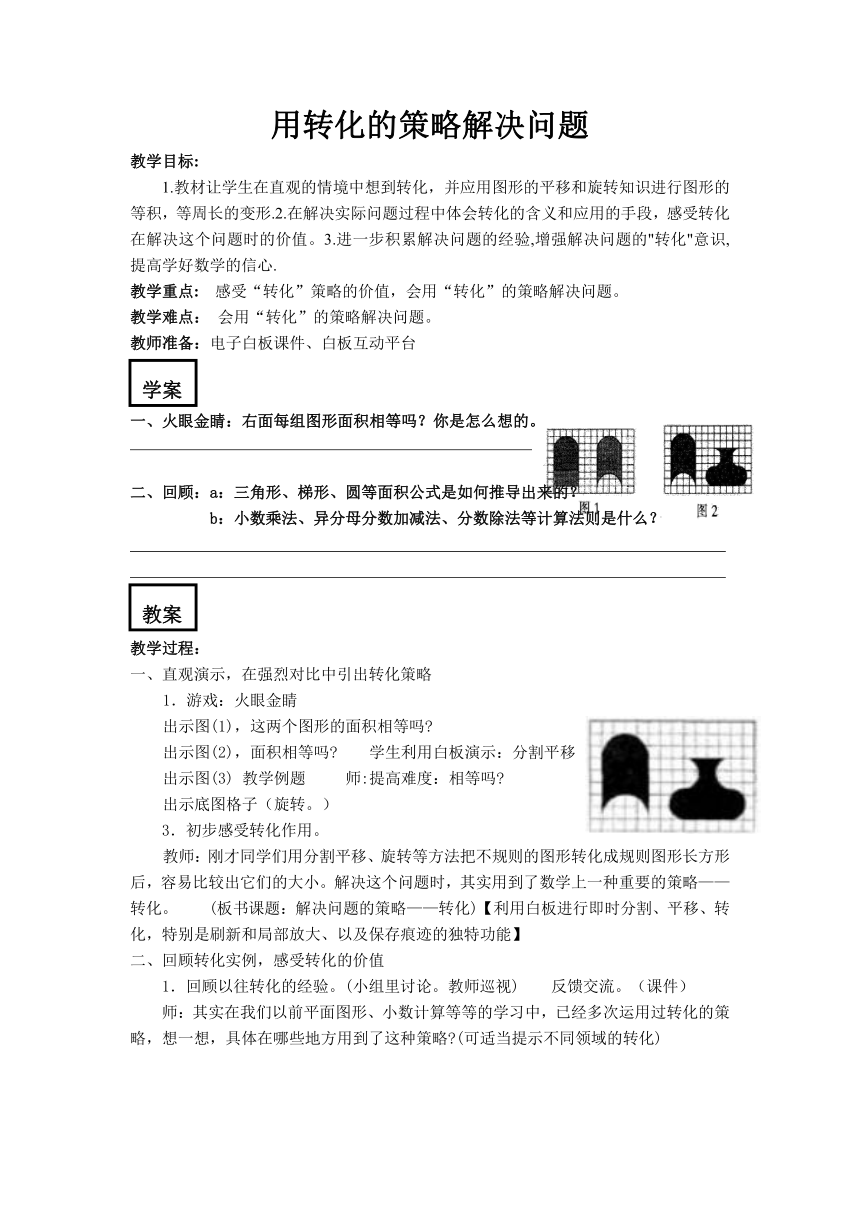
一、火眼金睛:右面每组图形面积相等吗?你是怎么想的。
二、回顾:a:三角形、梯形、圆等面积公式是如何推导出来的?
b:小数乘法、异分母分数加减法、分数除法等计算法则是什么?
教学过程:
一、直观演示,在强烈对比中引出转化策略
1.游戏:火眼金睛
出示图(1),这两个图形的面积相等吗?
出示图(2),面积相等吗? 学生利用白板演示:分割平移
出示图(3) 教学例题 师:提高难度:相等吗?
出示底图格子(旋转。)
3.初步感受转化作用。
教师:刚才同学们用分割平移、旋转等方法把不规则的图形转化成规则图形长方形后,容易比较出它们的大小。解决这个问题时,其实用到了数学上一种重要的策略——转化。 (板书课题:解决问题的策略——转化)【利用白板进行即时分割、平移、转化,特别是刷新和局部放大、以及保存痕迹的独特功能】
二、回顾转化实例,感受转化的价值
1.回顾以往转化的经验。(小组里讨论。教师巡视) 反馈交流。(课件)
师:其实在我们以前平面图形、小数计算等等的学习中,已经多次运用过转化的策略,想一想,具体在哪些地方用到了这种策略?(可适当提示不同领域的转化)
生可能会说:a、 面积或体积公式的推导过程中用过“形的转化”。(平行四边形→长方形;三角形、梯形→平行四边形;圆→长方形)b、 计算中用过数的转化(异分母分数加减法→同分母分数加减法;小数乘除法→整数乘除法;分数除法→分数乘法)
2、初步感受“转化”的价值。师:这些运用转化的策略解决问题的过程有什么共同点?(化繁为简、化难为易,化陌生的新问题为熟悉的问题) 板书:新问题→熟悉的问题 师:以后你再遇到一个陌生的问题时,你会怎样想呢?
三、运用转化的策略练习,学会一些转化的技巧
师:下面让我们带着智慧的火眼金睛,运用转化策略来解决一些问题。
(一)等积转化。 1.面积计算中的转化。 74页练习十四第2题。
师:这些图形形状虽然变了,但什么没变? (板书:等积转化。指出是图形转化中最常见的)
2.等周转化。
(1)蓝队与红队同时从同一地点,同时出发,速度相同。哪个队先到达终点?
学生在白板上操作, 现在能求出周长吗?
师:图形转化时什么没有变?(周长没有变) 所以这种图形转化属于“等周转化”。
(2)练习:74页练习十四第3题。(作业纸)
(二)数形转化
1.教学试一试。
观察算式,你有什么发现?相邻的两个分数有什么关系?
师:你会算吗?怎样算?(先通分)
师:通分就是把异分母分数转化成同分母分数,是数的转化。
师:其实,如果将这个算式转化为图形,更为有趣。(课件演示:逐步出示图形,表示算式)
观察图与算式,求这个算式的和就是求图中哪个部分的面积?(求涂色部分的面积)
因为用1减去空白部分就是涂色部分,所以算式的和可以转化为1-1/16。
师:本来算加法,比较繁;转化后,算减法,比较简单。所有的分数加法都能这样转化吗?这些加数有什么特征?
(2) 练习十四第1题。
数形结合展示比赛过程,得到结果。 (引导学生由“淘汰”进行思考) 〈设计意图:运用白板软件中的拉幕功能,让学生根据示意图的逐步提示,领会淘汰制的含义,通过图示找到被淘汰的队伍有15个。)
师:什么叫单场淘汰制?
追问:如果有64支球队按照这样的规则进行比赛,一共要进行多少场比赛?如果一共有n支球队呢?师:这里所做的是计数对象的转化。
四、全课总结,形成转化意识
通过今天的学习,你有什么收获? 数学家认为:解题就是把新题目转化为已经解过的题。
板书设计:
用转化策略解决问题
化难 为易
化繁 为简
化新 为旧
教学目标:
1.教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形.2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。3.进一步积累解决问题的经验,增强解决问题的"转化"意识,提高学好数学的信心.
教学重点: 感受“转化”策略的价值,会用“转化”的策略解决问题。
教学难点: 会用“转化”的策略解决问题。
教师准备:电子白板课件、白板互动平台
一、火眼金睛:右面每组图形面积相等吗?你是怎么想的。
二、回顾:a:三角形、梯形、圆等面积公式是如何推导出来的?
b:小数乘法、异分母分数加减法、分数除法等计算法则是什么?
教学过程:
一、直观演示,在强烈对比中引出转化策略
1.游戏:火眼金睛
出示图(1),这两个图形的面积相等吗?
出示图(2),面积相等吗? 学生利用白板演示:分割平移
出示图(3) 教学例题 师:提高难度:相等吗?
出示底图格子(旋转。)
3.初步感受转化作用。
教师:刚才同学们用分割平移、旋转等方法把不规则的图形转化成规则图形长方形后,容易比较出它们的大小。解决这个问题时,其实用到了数学上一种重要的策略——转化。 (板书课题:解决问题的策略——转化)【利用白板进行即时分割、平移、转化,特别是刷新和局部放大、以及保存痕迹的独特功能】
二、回顾转化实例,感受转化的价值
1.回顾以往转化的经验。(小组里讨论。教师巡视) 反馈交流。(课件)
师:其实在我们以前平面图形、小数计算等等的学习中,已经多次运用过转化的策略,想一想,具体在哪些地方用到了这种策略?(可适当提示不同领域的转化)
生可能会说:a、 面积或体积公式的推导过程中用过“形的转化”。(平行四边形→长方形;三角形、梯形→平行四边形;圆→长方形)b、 计算中用过数的转化(异分母分数加减法→同分母分数加减法;小数乘除法→整数乘除法;分数除法→分数乘法)
2、初步感受“转化”的价值。师:这些运用转化的策略解决问题的过程有什么共同点?(化繁为简、化难为易,化陌生的新问题为熟悉的问题) 板书:新问题→熟悉的问题 师:以后你再遇到一个陌生的问题时,你会怎样想呢?
三、运用转化的策略练习,学会一些转化的技巧
师:下面让我们带着智慧的火眼金睛,运用转化策略来解决一些问题。
(一)等积转化。 1.面积计算中的转化。 74页练习十四第2题。
师:这些图形形状虽然变了,但什么没变? (板书:等积转化。指出是图形转化中最常见的)
2.等周转化。
(1)蓝队与红队同时从同一地点,同时出发,速度相同。哪个队先到达终点?
学生在白板上操作, 现在能求出周长吗?
师:图形转化时什么没有变?(周长没有变) 所以这种图形转化属于“等周转化”。
(2)练习:74页练习十四第3题。(作业纸)
(二)数形转化
1.教学试一试。
观察算式,你有什么发现?相邻的两个分数有什么关系?
师:你会算吗?怎样算?(先通分)
师:通分就是把异分母分数转化成同分母分数,是数的转化。
师:其实,如果将这个算式转化为图形,更为有趣。(课件演示:逐步出示图形,表示算式)
观察图与算式,求这个算式的和就是求图中哪个部分的面积?(求涂色部分的面积)
因为用1减去空白部分就是涂色部分,所以算式的和可以转化为1-1/16。
师:本来算加法,比较繁;转化后,算减法,比较简单。所有的分数加法都能这样转化吗?这些加数有什么特征?
(2) 练习十四第1题。
数形结合展示比赛过程,得到结果。 (引导学生由“淘汰”进行思考) 〈设计意图:运用白板软件中的拉幕功能,让学生根据示意图的逐步提示,领会淘汰制的含义,通过图示找到被淘汰的队伍有15个。)
师:什么叫单场淘汰制?
追问:如果有64支球队按照这样的规则进行比赛,一共要进行多少场比赛?如果一共有n支球队呢?师:这里所做的是计数对象的转化。
四、全课总结,形成转化意识
通过今天的学习,你有什么收获? 数学家认为:解题就是把新题目转化为已经解过的题。
板书设计:
用转化策略解决问题
化难 为易
化繁 为简
化新 为旧
