浙教版信息技术选修1 5.4 查找算法的程序实现 课件(共20张PPT)
文档属性
| 名称 | 浙教版信息技术选修1 5.4 查找算法的程序实现 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 386.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览







文档简介
查找算法的程序实现
价格猜猜猜小游戏
课堂思考
问题一:你用什么方法猜出所有的价格,大概描述下?
?
?
问题二:怎么样能用尽量少的次数猜出三件商品的价格?
(1)对分查找是效率很高的查找方法,但被查找的数据必须是有序的。
对分查找的原理和方法
(2)首先将查找的数与有序数组内处于中间位置的数据比较,如果中间位置上的数与查找的数不同,根据有序性,就可确定应该在数组的前半部分还是后半部分继续查找。
(3)在新确定的范围内,继续按上述方法进行查找,直到获得最终结果。
举 例
d(1)
22
d(2)
28
d(3)
30
d(4)
33
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明:
1、d(1 to 10)数组来存放一组升序序列数据;
2、i表示查找范围的第一个数组元素的下标;
3、j表示最后一个数组元素的下标;
4、mid表示中间位置元素的下标;
5、key保存要查找的数。
← i
←mid=fix((i+j)/2)
← j
情况一:要找的值在后半部分,如要查找数key=55
① 第一次查找 d(1)---d(10) key=55
则i=1; j=10; mid=fix((1+10)/2)(mid=5)
d(1)
22
← i
d(2)
28
d(3)
30
d(4)
33
d(5)
38
←mid=fix((i+j)/2)
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
← j
key>d(mid) 说明key在后半部分;i=mid+1 (i=6); j不变。
Key>d(mid)
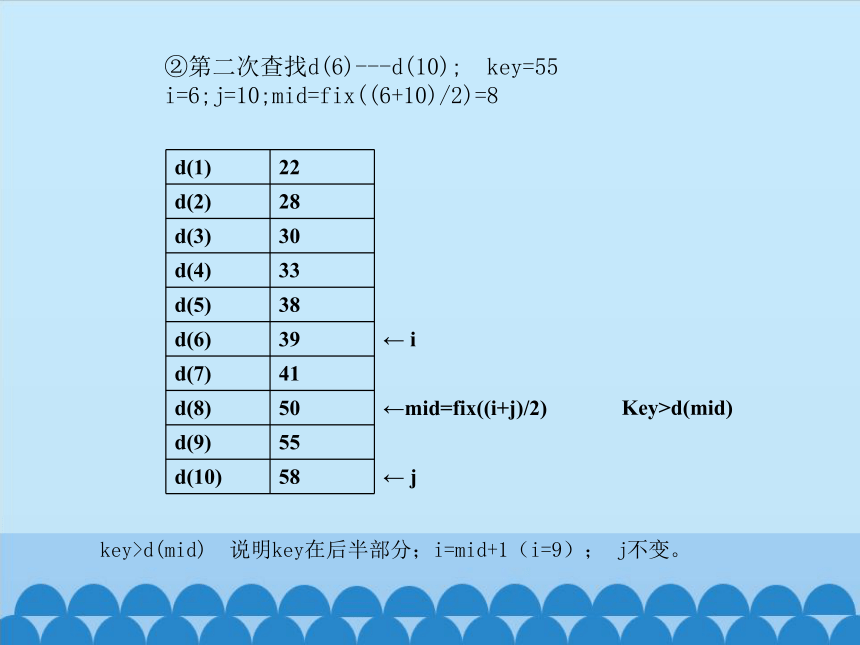
②第二次查找d(6)---d(10); key=55
i=6;j=10;mid=fix((6+10)/2)=8
d(1)
22
d(2)
28
d(3)
30
d(4)
33
d(5)
38
d(6)
39
← i
d(7)
41
d(8)
50
←mid=fix((i+j)/2)
d(9)
55
d(10)
58
← j
key>d(mid) 说明key在后半部分;i=mid+1(i=9); j不变。
Key>d(mid)
③第三次查找d(9)---d(10) key=55
i=9;j=10;mid=fix((9+10)/2) ( mid=9)
d(1)
22
d(2)
28
d(3)
30
d(4)
33
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
← i
←mid=fix((i+j)/2)
d(10)
58
← j
key=d(mid) 说明找到了。
总结一:如果key>d(mid) ,新查找的范围为下半部分, j值不变,i=mid+1。
Key=d(mid)
情况二:要找的值在前半部分,如要查找数key=28
① 第一次查找d(1)---d(10) key=28
i=1;j=10;mid=fix((1+10)/2)=5;
d(1)
22
← i
d(2)
28
d(3)
30
d(4)
33
d(5)
38
←mid=fix((i+j)/2)
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
← j
keyKey②第二次查找d(1)---d(4) key=28
i=1;j=4;mid=fix((1+4)/2) (mid=2)
d(1)
22
← i
d(2)
28
←mid=fix((i+j)/2)
d(3)
30
d(4)
33
← j
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
key=d(mid) ;说明找到了。
总结二:如果keyKey=d(mid)
情况三:要找的值找不到,以查找键KEY=29为例分析:
① 第一次查找d(1)---d(10); KEY=29
i=1;j=10;mid=fix((1+10)/2)=5;
d(1)
22
← i
d(2)
28
d(3)
30
d(4)
33
d(5)
38
←mid=fix((i+j)/2)
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
← j
说明key在前半部分;j=mid-1(j=4)。
Key②第二次查找 KEY=29 d(1)---d(4)
i=1;j=4;mid=fix((1+4)/2)=2;
d(1)
22
← i
d(2)
28
←mid=fix((i+j)/2)
d(3)
30
d(4)
33
← j
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明key在后半部分;i=mid+1(i=3)。
Key>d(mid)
③第三次查找 key =29 d (3)---d (4)
i=3;j=4;mid=fix((3+4)/2)=3;
d(1)
22
d(2)
28
d(3)
30
← i
←mid=fix((i+j)/2)
d(4)
33
← j
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明key在前半部分;j=mid-1(j=3) 。
Key③第四次查找 key =29 d (3)---d (3)
i=3;j=3;mid=fix((3+3)/2)=3;
d(1)
22
d(2)
28
d(3)
30
← i
←mid=fix((i+j)/2)
← j
d(4)
33
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明key在前半部分;j=mid-1(j=2)
总结三:i>j时找不到了,查找结束。
Key归纳分析
总结三 在i<=j时重复查找,如果找到,退出查找;如果i>j还是找不到,查找也会结束。
总结二 如果key总结一 如果key>d(mid) ,新查找的范围为下半部分,j值不变,i=mid+1;
语句①
If key>d(mid) then
语句②
Elseif key语句③
Else
‘输出找到的结果
exit do
endif
Do while i<=j
Loop
If i>j then 输出找不到的结果
mid=fix((i+j)/2)
i=mid+1
j=mid-1
课堂任务一
将任务一内,查找按钮上空缺的代码补上,使之能在输入数的个数后,产生指定个数的随机数,并能找到数组里的任一个数, 输出这个数位于哪个数组中;如果所找数字不在数组中,则输出”找不到”。
课堂任务二
完成任务一的基础上,添加一个text3文本框,使其能显示查找的总次数,效果图如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数组中数的个数
1
2
3
4
5
6
7
8
16
31
65
128
256
查找最多的次数
?1
?2
?2
?3
3?
?3
?3
?4
5?
5?
?6
?8
9?
不同的数组个数所对应的最大次数在如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数组中数的个数
300
400
500
511
512
999
1023
1024
1500
2000
查找最多的次数
9
?9
?9
?9
10?
?10
10
11
11
11
最多次数c和个数n满足如下公式:
c=log2n+1 (取整数部分)
(1)采用对分查找的前提是数据序列必须是有序。
(2)对分查找的程序实现是通过DO循环中的i和j的大小比较来控制循环次数,块IF语句来控制i和j值的变化从而实现查找范围的一步步缩小。
(3)由于对分查找过程中的每次比较都能使得搜索空间减半,对分查找将不会使用超过log2n+1次来找到目标值。
课堂小结
谢 谢
价格猜猜猜小游戏
课堂思考
问题一:你用什么方法猜出所有的价格,大概描述下?
?
?
问题二:怎么样能用尽量少的次数猜出三件商品的价格?
(1)对分查找是效率很高的查找方法,但被查找的数据必须是有序的。
对分查找的原理和方法
(2)首先将查找的数与有序数组内处于中间位置的数据比较,如果中间位置上的数与查找的数不同,根据有序性,就可确定应该在数组的前半部分还是后半部分继续查找。
(3)在新确定的范围内,继续按上述方法进行查找,直到获得最终结果。
举 例
d(1)
22
d(2)
28
d(3)
30
d(4)
33
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明:
1、d(1 to 10)数组来存放一组升序序列数据;
2、i表示查找范围的第一个数组元素的下标;
3、j表示最后一个数组元素的下标;
4、mid表示中间位置元素的下标;
5、key保存要查找的数。
← i
←mid=fix((i+j)/2)
← j
情况一:要找的值在后半部分,如要查找数key=55
① 第一次查找 d(1)---d(10) key=55
则i=1; j=10; mid=fix((1+10)/2)(mid=5)
d(1)
22
← i
d(2)
28
d(3)
30
d(4)
33
d(5)
38
←mid=fix((i+j)/2)
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
← j
key>d(mid) 说明key在后半部分;i=mid+1 (i=6); j不变。
Key>d(mid)
②第二次查找d(6)---d(10); key=55
i=6;j=10;mid=fix((6+10)/2)=8
d(1)
22
d(2)
28
d(3)
30
d(4)
33
d(5)
38
d(6)
39
← i
d(7)
41
d(8)
50
←mid=fix((i+j)/2)
d(9)
55
d(10)
58
← j
key>d(mid) 说明key在后半部分;i=mid+1(i=9); j不变。
Key>d(mid)
③第三次查找d(9)---d(10) key=55
i=9;j=10;mid=fix((9+10)/2) ( mid=9)
d(1)
22
d(2)
28
d(3)
30
d(4)
33
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
← i
←mid=fix((i+j)/2)
d(10)
58
← j
key=d(mid) 说明找到了。
总结一:如果key>d(mid) ,新查找的范围为下半部分, j值不变,i=mid+1。
Key=d(mid)
情况二:要找的值在前半部分,如要查找数key=28
① 第一次查找d(1)---d(10) key=28
i=1;j=10;mid=fix((1+10)/2)=5;
d(1)
22
← i
d(2)
28
d(3)
30
d(4)
33
d(5)
38
←mid=fix((i+j)/2)
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
← j
key
i=1;j=4;mid=fix((1+4)/2) (mid=2)
d(1)
22
← i
d(2)
28
←mid=fix((i+j)/2)
d(3)
30
d(4)
33
← j
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
key=d(mid) ;说明找到了。
总结二:如果key
情况三:要找的值找不到,以查找键KEY=29为例分析:
① 第一次查找d(1)---d(10); KEY=29
i=1;j=10;mid=fix((1+10)/2)=5;
d(1)
22
← i
d(2)
28
d(3)
30
d(4)
33
d(5)
38
←mid=fix((i+j)/2)
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
← j
说明key在前半部分;j=mid-1(j=4)。
Key
i=1;j=4;mid=fix((1+4)/2)=2;
d(1)
22
← i
d(2)
28
←mid=fix((i+j)/2)
d(3)
30
d(4)
33
← j
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明key在后半部分;i=mid+1(i=3)。
Key>d(mid)
③第三次查找 key =29 d (3)---d (4)
i=3;j=4;mid=fix((3+4)/2)=3;
d(1)
22
d(2)
28
d(3)
30
← i
←mid=fix((i+j)/2)
d(4)
33
← j
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明key在前半部分;j=mid-1(j=3) 。
Key
i=3;j=3;mid=fix((3+3)/2)=3;
d(1)
22
d(2)
28
d(3)
30
← i
←mid=fix((i+j)/2)
← j
d(4)
33
d(5)
38
d(6)
39
d(7)
41
d(8)
50
d(9)
55
d(10)
58
说明key在前半部分;j=mid-1(j=2)
总结三:i>j时找不到了,查找结束。
Key
总结三 在i<=j时重复查找,如果找到,退出查找;如果i>j还是找不到,查找也会结束。
总结二 如果key
语句①
If key>d(mid) then
语句②
Elseif key
Else
‘输出找到的结果
exit do
endif
Do while i<=j
Loop
If i>j then 输出找不到的结果
mid=fix((i+j)/2)
i=mid+1
j=mid-1
课堂任务一
将任务一内,查找按钮上空缺的代码补上,使之能在输入数的个数后,产生指定个数的随机数,并能找到数组里的任一个数, 输出这个数位于哪个数组中;如果所找数字不在数组中,则输出”找不到”。
课堂任务二
完成任务一的基础上,添加一个text3文本框,使其能显示查找的总次数,效果图如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数组中数的个数
1
2
3
4
5
6
7
8
16
31
65
128
256
查找最多的次数
?1
?2
?2
?3
3?
?3
?3
?4
5?
5?
?6
?8
9?
不同的数组个数所对应的最大次数在如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}数组中数的个数
300
400
500
511
512
999
1023
1024
1500
2000
查找最多的次数
9
?9
?9
?9
10?
?10
10
11
11
11
最多次数c和个数n满足如下公式:
c=log2n+1 (取整数部分)
(1)采用对分查找的前提是数据序列必须是有序。
(2)对分查找的程序实现是通过DO循环中的i和j的大小比较来控制循环次数,块IF语句来控制i和j值的变化从而实现查找范围的一步步缩小。
(3)由于对分查找过程中的每次比较都能使得搜索空间减半,对分查找将不会使用超过log2n+1次来找到目标值。
课堂小结
谢 谢
同课章节目录
- 第一章 算法和算法的表示
- 1.1 使用计算机解决问题的一般过程
- 1.2 确定解决问题的方法
- 1.3 把解决问题的方法步骤化
- 1.4 算法的概念和表示方法
- 第二章 算法实例
- 2.1 枚举算法
- 2.2 解析算法
- 2.3 排序
- 2.4 查找
- 第三章 面向对象程序设计的基本知识
- 3.1 面向对象程序设计方法简介
- 3.2 在可视化的程序设计环境VB中建立一个应用程序
- 第四章 VB程序设计初步
- 4.1 基本数据类型、常量、变量
- 4.2 基本运算和表达式
- 4.3 语句
- 4.4 过程和函数
- 第五章 算法实例的程序实现
- 5.1 枚举算法的程序实现
- 5.2 解析算法的程序实现
- 5.3 排序算法的程序实现
- 5.4 查找算法的程序实现
- 5.5 递归算法实例及程序实现
- 非试题类资料
