河南省长垣市第十中学2020-2021学年高一12月考数学word含答案
文档属性
| 名称 | 河南省长垣市第十中学2020-2021学年高一12月考数学word含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 522.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 17:40:22 | ||
图片预览



文档简介
数学
一、单选题
1.(5分)设集合,则(
)
A.
B.
C.
D.
2.(5分)下列函数f(x)中,满足“对任意x1、x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
A.f(x)=(x﹣1)2
B.f(x)=ex
C.f(x)=
D.f(x)=ln(x+1)
3.(5分)对于给定的函数,给出五个命题其中真命题是(
)
①函数的图象关于原点对称;②函数在上具有单调性;③函数的图象关于轴对称;④函数的最大值是0.
A.①②③
B.①③④
C.②③④
D.①②④
4.(5分)函数
在区间上的最大值比最小值大,则实数的值为(
)
A.
B.
C.
D.
5.(5分)已知函数,其反函数为,若,则的值为( )
A.2
B.1
C.
D.
6.(5分)函数y=log2的定义域(
)
A.(,3)
B.(,+∞)
C.(,3)
D.[,3]
7.(5分)若方程有一个正根和一个负根,则实数的取值范围是(
)A.或
B.
C.
D.
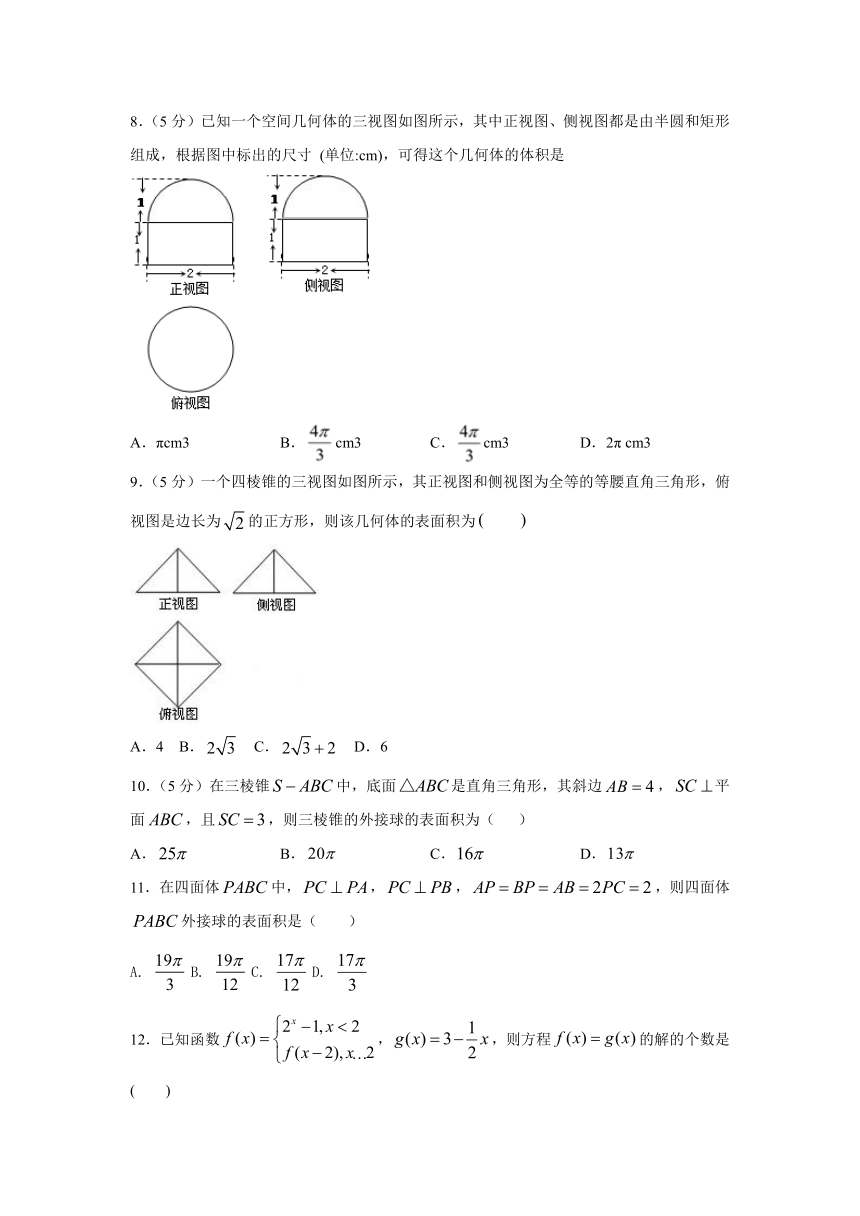
8.(5分)已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸
(单位:cm),可得这个几何体的体积是
A.πcm3
B.cm3
C.cm3
D.2π
cm3
9.(5分)一个四棱锥的三视图如图所示,其正视图和侧视图为全等的等腰直角三角形,俯视图是边长为的正方形,则该几何体的表面积为
A.4
B.
C.
D.6
10.(5分)在三棱锥中,底面是直角三角形,其斜边,平面,且,则三棱锥的外接球的表面积为(
)
A.
B.
C.
D.
11.在四面体中,,,,则四面体外接球的表面积是(
)
A.
B.
C.
D.
12.已知函数,,则方程的解的个数是(
)
A.
B.
C.
D.
二、填空题
13.(5分)已知集合,且,则的值为___________.
14.(5分)如图所示是一个三棱柱的三视图,则这个三棱柱的体积为______
(5分)若全集为实数集,,则________
(5分)设函数,若对任意的,恒成立,则的取值范围是__________.
三、解答题
17.(10分)集合,,求
,,.
18.(12分)函数的图象经过点和.
(1)求函数的解析式;
(2)函数,求函数的最小值.
19.(12分)已知是定义在上的奇函数,且.
(1)求的解析式;
(2)设,求在上的最大值与最小值.
20.(12分)如图所示,圆锥的底面圆半径,其侧面展开图是一个圆心角为的扇形.
(1)求此圆锥的表面积;(2)求此圆锥的体积.
21.(12分)已知函数,其中为自然对数的底数.
(1)证明:在上单调递增;
(2)函数,如果总存在,对任意都成立,求实数的取值范围.
22.(12分)若函数为奇函数.
(1)求a的值;(2)求函数的定义域;(3)求函数的值域.
参考答案
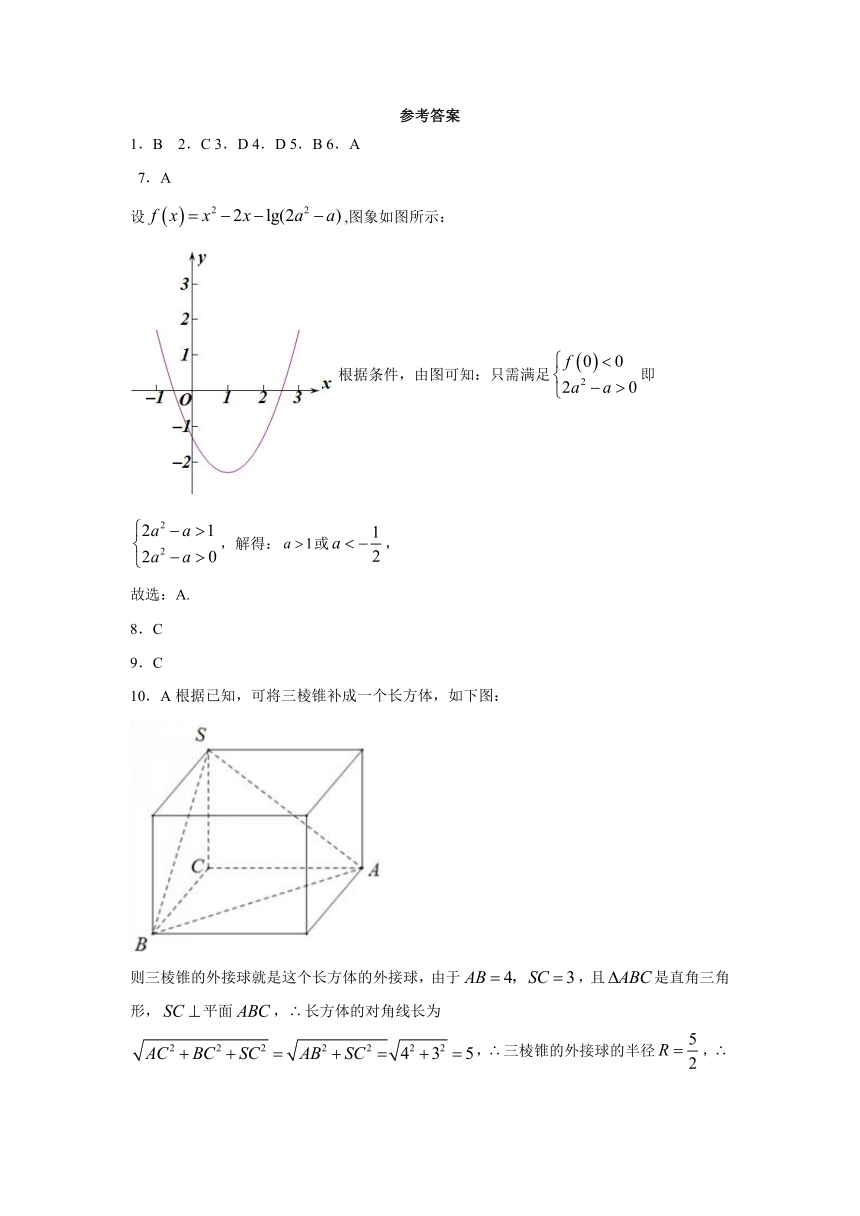
B
2.C
3.D
4.D
5.B
6.A
7.A
设,图象如图所示:
根据条件,由图可知:只需满足即,解得:或,
故选:A.
C
C
10.A根据已知,可将三棱锥补成一个长方体,如下图:
则三棱锥的外接球就是这个长方体的外接球,由于,且是直角三角形,平面,长方体的对角线长为,三棱锥的外接球的半径,三棱锥的外接球的表面积为,故选A.
11.A
∵,,平面,
∴平面.
如图,设是外接球球心,是的中心,
则平面,
,,
则,
故四面体外接球的表面积是.
故选A.
12.C
【详解】
根据的解析式知,在区间,,,,()上的图象相同,作出函数图象,如图,同时作出的图象,它是一条直线,由于,,,因此它们有4个交点.即方程有4个解.
故选:C.
13.3
∵,∴,
由,若,则,此时,舍去,
∴,解得(舍去),此时,
由,又,∴,,
∴.
故答案为:3.
14.cm2
15.
16.
解析
由题意可知,函数的定义域为R.
∵
∴函数为定义在R上的奇函数.
∵当时,函数且在上为增函数
∴当时,函数在上为减函数
∴函数在上为减函数.
∵,且为定义在R上的奇函数
∴函数为R上的减函数(注意函数在原点处连续).
∵,∴
∴,,∵,∴,∴≤1.
∴≤e,即的取值范围是.
17.………………………………………2分
……………………………4分
…………………………………6分
……………………………………9分
……………………………………12分
18.(1);(2)
(1)由题意得,解得.
所以.
(2)设,则,即,
所以当,即时,.
19.(1);(2)最大值,最小值
(1)∵是奇函数,
∴,解得,
,,∴;
(2)由(1),对称轴为,
∵,
∴,.
20.(1);(2)(1)因为,所以底面圆周长为,所以底面圆的面积为,
所以弧长为,
又因为,则有,所以,扇形ASB的面积为,所以圆锥的表面积=
(2)在中,.
,所以圆锥的体积.
21.(1)证明见解析;(2)
(1)设,
则
,
∵,∴,,∴,即,
∴在上单调递增;
(2)总存在,对任意都成立,即,
的最大值为,
是偶函数,在是增函数,∴当时,,
∴,整理得,,
∵,∴,即,∴,∴.即的取值范围是.
22.(1);(2){x|x≠0};(3)或.
函数y=f(x)==a-.
(1)由奇函数的定义,可得f(-x)+f(x)=0,即2a--=0,∴a=-.
(2)∵y=--,∴3x-1≠0,即x≠0.
∴函数y=--的定义域为{x|x≠0}.
(3)∵x≠0,∴3x-1≠0,∴0>3x-1>-1或3x-1>0.
∴-->或--<-.即函数的值域为.
一、单选题
1.(5分)设集合,则(
)
A.
B.
C.
D.
2.(5分)下列函数f(x)中,满足“对任意x1、x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
A.f(x)=(x﹣1)2
B.f(x)=ex
C.f(x)=
D.f(x)=ln(x+1)
3.(5分)对于给定的函数,给出五个命题其中真命题是(
)
①函数的图象关于原点对称;②函数在上具有单调性;③函数的图象关于轴对称;④函数的最大值是0.
A.①②③
B.①③④
C.②③④
D.①②④
4.(5分)函数
在区间上的最大值比最小值大,则实数的值为(
)
A.
B.
C.
D.
5.(5分)已知函数,其反函数为,若,则的值为( )
A.2
B.1
C.
D.
6.(5分)函数y=log2的定义域(
)
A.(,3)
B.(,+∞)
C.(,3)
D.[,3]
7.(5分)若方程有一个正根和一个负根,则实数的取值范围是(
)A.或
B.
C.
D.
8.(5分)已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸
(单位:cm),可得这个几何体的体积是
A.πcm3
B.cm3
C.cm3
D.2π
cm3
9.(5分)一个四棱锥的三视图如图所示,其正视图和侧视图为全等的等腰直角三角形,俯视图是边长为的正方形,则该几何体的表面积为
A.4
B.
C.
D.6
10.(5分)在三棱锥中,底面是直角三角形,其斜边,平面,且,则三棱锥的外接球的表面积为(
)
A.
B.
C.
D.
11.在四面体中,,,,则四面体外接球的表面积是(
)
A.
B.
C.
D.
12.已知函数,,则方程的解的个数是(
)
A.
B.
C.
D.
二、填空题
13.(5分)已知集合,且,则的值为___________.
14.(5分)如图所示是一个三棱柱的三视图,则这个三棱柱的体积为______
(5分)若全集为实数集,,则________
(5分)设函数,若对任意的,恒成立,则的取值范围是__________.
三、解答题
17.(10分)集合,,求
,,.
18.(12分)函数的图象经过点和.
(1)求函数的解析式;
(2)函数,求函数的最小值.
19.(12分)已知是定义在上的奇函数,且.
(1)求的解析式;
(2)设,求在上的最大值与最小值.
20.(12分)如图所示,圆锥的底面圆半径,其侧面展开图是一个圆心角为的扇形.
(1)求此圆锥的表面积;(2)求此圆锥的体积.
21.(12分)已知函数,其中为自然对数的底数.
(1)证明:在上单调递增;
(2)函数,如果总存在,对任意都成立,求实数的取值范围.
22.(12分)若函数为奇函数.
(1)求a的值;(2)求函数的定义域;(3)求函数的值域.
参考答案
B
2.C
3.D
4.D
5.B
6.A
7.A
设,图象如图所示:
根据条件,由图可知:只需满足即,解得:或,
故选:A.
C
C
10.A根据已知,可将三棱锥补成一个长方体,如下图:
则三棱锥的外接球就是这个长方体的外接球,由于,且是直角三角形,平面,长方体的对角线长为,三棱锥的外接球的半径,三棱锥的外接球的表面积为,故选A.
11.A
∵,,平面,
∴平面.
如图,设是外接球球心,是的中心,
则平面,
,,
则,
故四面体外接球的表面积是.
故选A.
12.C
【详解】
根据的解析式知,在区间,,,,()上的图象相同,作出函数图象,如图,同时作出的图象,它是一条直线,由于,,,因此它们有4个交点.即方程有4个解.
故选:C.
13.3
∵,∴,
由,若,则,此时,舍去,
∴,解得(舍去),此时,
由,又,∴,,
∴.
故答案为:3.
14.cm2
15.
16.
解析
由题意可知,函数的定义域为R.
∵
∴函数为定义在R上的奇函数.
∵当时,函数且在上为增函数
∴当时,函数在上为减函数
∴函数在上为减函数.
∵,且为定义在R上的奇函数
∴函数为R上的减函数(注意函数在原点处连续).
∵,∴
∴,,∵,∴,∴≤1.
∴≤e,即的取值范围是.
17.………………………………………2分
……………………………4分
…………………………………6分
……………………………………9分
……………………………………12分
18.(1);(2)
(1)由题意得,解得.
所以.
(2)设,则,即,
所以当,即时,.
19.(1);(2)最大值,最小值
(1)∵是奇函数,
∴,解得,
,,∴;
(2)由(1),对称轴为,
∵,
∴,.
20.(1);(2)(1)因为,所以底面圆周长为,所以底面圆的面积为,
所以弧长为,
又因为,则有,所以,扇形ASB的面积为,所以圆锥的表面积=
(2)在中,.
,所以圆锥的体积.
21.(1)证明见解析;(2)
(1)设,
则
,
∵,∴,,∴,即,
∴在上单调递增;
(2)总存在,对任意都成立,即,
的最大值为,
是偶函数,在是增函数,∴当时,,
∴,整理得,,
∵,∴,即,∴,∴.即的取值范围是.
22.(1);(2){x|x≠0};(3)或.
函数y=f(x)==a-.
(1)由奇函数的定义,可得f(-x)+f(x)=0,即2a--=0,∴a=-.
(2)∵y=--,∴3x-1≠0,即x≠0.
∴函数y=--的定义域为{x|x≠0}.
(3)∵x≠0,∴3x-1≠0,∴0>3x-1>-1或3x-1>0.
∴-->或--<-.即函数的值域为.
同课章节目录
