河南省周口市西华县第一高级中学2020-2021学年高一上学期第七次周考(1月)数学(理)试题 Word版含答案
文档属性
| 名称 | 河南省周口市西华县第一高级中学2020-2021学年高一上学期第七次周考(1月)数学(理)试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 442.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 11:27:55 | ||
图片预览




文档简介
1189990012433300西华一高52届高一上期第七次周考数学试卷(理科)(1.9)
(时间:120分钟,满分:150分)
选择题(本大题共12小题,每小题5分,共60分。给出的四个选项中,只有一项是符合题目要求的.)
1. 下列说法正确的是( )
A. 棱柱被平面分成的两部分可以都是棱柱
B. 底面是矩形的平行六面体是长方体
C. 棱柱底面一定是平行四边形
D. 棱锥的底面一定是三角形
2. 直线l1的倾斜角false,直线l1⊥l2,则直线l2的斜率为( )
A. -false B. false C. -false D. false
3. 如果AB>0,BC>0,那么直线Ax-By-C=0不经过的象限是( )
4343400205740A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 如图,AB是⊙O直径,C是圆周上不同于A、B的任意一点,PA与
平面ABC垂直,则四面体P_ABC的四个面中,直角三角形的个数有( )
A. 4个 B. 3个 C. 1个 D. 2个
5. 轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( )
A. 4倍 B. 3倍 C. false 倍 D. 2倍
6. 已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:
①若m∥α,m∥β,则α∥β
②若m?α,n?α,m∥β,n∥β,则α∥β;
③m?α,n?β,m、n是异面直线,那么n与α相交;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β.
其中正确的命题是( )
A ①② B. ②③ C. ③④ D. ④
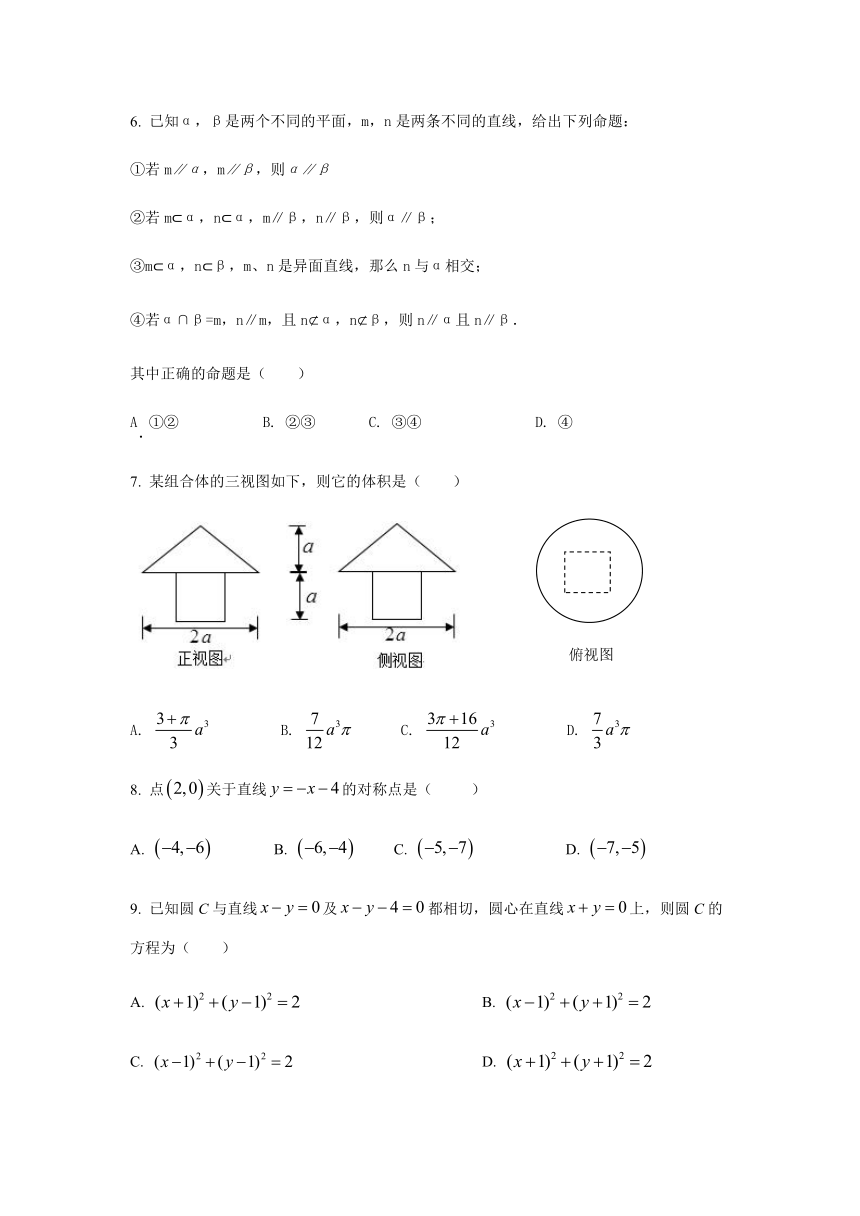
7. 某组合体的三视图如下,则它的体积是( )
3822065347345
357378058420
37572951083310俯视图
俯视图
A. false B. false C. false D. false
8. 点false关于直线false的对称点是( )
A. false B. false C. false D. false
9. 已知圆C与直线false及false都相切,圆心在直线false上,则圆C的方程为( )
A. false B. false
C. false D. false
10. 已知在四面体false中,false分别是false的中点,false,
则false与false所成角的度数为( )
A. false0 B. false0 C. false0 D. false0
402907549149011. 如图,在正三棱柱false中,false,若二面角false的大小为false,则点C到平面false的距离为( )
A. 1 B. false C. false D. false
12. 已知函数false若a,b,c互不相等,且false,则false的取值范围是( )
A.false B.false C.false D.false
填空题(本大题共4小题,每小题5分,共20分。答案填在答题卡对应题号后的横线上.)
直线false过点false且与以点false为端点的线段恒相交,则false的斜率取值范围是 .
14. 若两平行直线2x+y-4=0与y =-2x-k-2的距离不大于false,则实数k的取值范围是____.
15. 若直线l在x轴上的截距为1,点false到l的距离相等,则l的方程为_____.
16. 若三棱锥false中,false,其余各棱长均为5,则三棱锥内切球的表面积__.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
(1)false
(2)false
18. (本小题满分12分)
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,E为AD的中点,过A,D,N的平面交PC于点M. 求证: (1)EN∥平面PDC;
366712587630(2)BC⊥平面PEB;
(3)平面PBC⊥平面ADM
19.(本小题满分12分)
已知直线l过点P(1,1),并与直线l1:x-y+3=0和l2:2x+y-6=0分别交于点A、B,若线段AB被点P平分,求:
(1)直线l的方程;
(2)以坐标原点O为圆心且被l截得的弦长为false的圆的方程.
20. (本小题满分12分)
3600450417195如图,false平面false,false,false,false,false分别为false的中点.
(I)证明:false平面false;
(II)求false与平面false所成角的正弦值。
21.(本小题满分12分)
新能源开发能够有效地解决我国能源短缺和传统能源使用带来的环境污染问题,国家新能源政策的出台,给新能源产业带来了春天,已知某新能源企业,年固定成本600万,每生产false台设备,另需投入成本t万元,若年产量不足100台,则false;若年产量不小于100台,则false,每台设备售价150万元,通过市场分析,该企业生产的设备能全部售完.
(1)写出年利润y(万元)关于年产量x(台)的关系式;
(2)年产量为多少台时,该企业所获利润最大?
(本小题满分12分)
3276600758190如图,已知false平面false,四边形false为矩形,四边形false为直角梯形,false,AB∥CD,false,false.
(1)求证:false平面false;
(2)求三棱锥false的体积.
西华一高52届高一上期第七次周考数学参考答案(理科)
1.【答案】A【解析】对于B.底面是矩形的平行六面体,它的侧面不一定是矩形,故它也不一定是长方体,故B错;对于C.棱柱的底面是平面多边形,不一定是平行四边形,故C错;对于D.棱锥的底面是平面多边形,不一定是三角形,故D错;故选A.
2.【答案】C【解析】如图:直线L1的倾斜角α1=30°,直线L1⊥L2,则L2的倾斜角等于30°+90°=120°,∴L2的斜率为 tan120°=﹣tan60°false,故选C.
3.【答案】B【解析】:斜率为false,截距false,故不过第二象限.
4.【答案】A【解析】∵AB是圆O的直径,∴∠ACB=false,即false,三角形false是直角三角形.又∵false圆O所在的平面,∴三角形false和三角形false是直角三角形,且BC在此平面中,∴false平面false,∴三角形false是直角三角形.综上,三角形false,三角形false,三角形false,三角形false.直角三角形数量为4.故选:A.
5.【答案】D【解析】圆锥的轴截面是正三角形,设底面半径为r,则它的底面积为πr2;
圆锥的侧面积为:false2rπ?2r=2πr2;圆锥的侧面积是底面积的2倍.
6. 【答案】D【解析】①若m∥α,m∥β,则α∥β或α与β相交,错误命题;
②若m?α,n?α,m∥β,n∥β,则α∥β或α与β相交.错误的命题;
③m?α,n?β,m、n是异面直线,那么n与α相交,也可能n∥α,是错误命题;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β.是正确的命题.
7. 【答案】A【解析】:falsefalse,故选A.
8. 【答案】A【解析】设对称点为false,则false ,则false,故选A.
9. 【答案】B【解析】圆心在false上,圆心的纵横坐标值相反,显然能排除C、D;
验证:A中圆心false到两直线false的距离是false;
圆心false到直线false的距离是false.故A错误.
10. 【答案】A【解析】略
11. 【答案】C【解析】取false的中点false,连接false和false,根据二面角的定义,false.
由题意得false,所以false,false.
设false到平面false的距离为false,易知三棱锥false的体积三棱锥false的体积相等,
即false,解得false,故点C到平面false的距离为false.
12. 【答案】A【详解】作出函数false的图象如图所示:
令false,由图知:false,结合图象,不妨令false,以false,false,false ,false,false,false,所以false,
13.【解析】∵false
∴false
根据如下图形可知,
使直线false与线段false相交的斜率取值范围是false
14. 【答案】false
【解析】y=﹣2x﹣k﹣2的一般式方程为2x+y+k+2=0
则两平行直线的距离dfalse
得,|k+6|≤5,解得﹣11≤k≤﹣1,
当k+2=﹣4,即k=﹣6,此时两直线重合,
所以k的取值范围是false
15. 【答案】false或false
【解析】显然直线false轴时符合要求,此时false的方程为false.
当直线l的斜率存在时,设直线l的斜率为k,则l的方程为false,
即false.∵A,B到l的距离相等
∴false,∴false,∴false,
∴直线l的方程为false.故答案为false或false
16. 【答案】false
【解析】由题意得,易知内切球球心false到各面距离相等,
设false为false的中点,则false在false上且false为false的中点,
在false中,false,
所以三棱锥内切球的表面积为false.
17. 【解析】(1)false
falsefalse
falsefalse
(2)原式false
false.
18. 【解析】
(1)∵AD∥BC,BC?平面PBC,
AD?平面PBC,
∴AD∥平面PBC.又平面ADMN∩平面PBC=MN,∴AD∥MN.又∵AD∥BC,∴MN∥BC.
又∵N为PB的中点,∴M为PC的中点,
∴MN=falseBC.
∵E为AD的中点,DE=falseAD=falseBC=MN,
∴DEfalseMN,∴四边形DENM为平行四边形,
∴EN∥DM.又∵EN?平面PDC,DM?平面PDC,
∴EN∥平面PDC.
(2)∵四边形ABCD是边长为2的菱形,且∠BAD=60°,E为AD中点,
∴BE⊥AD.又∵PE⊥AD,PE∩BE=E,∴AD⊥平面PEB.∵AD∥BC,∴BC⊥平面PEB.
(3)由(2)知AD⊥PB.
又∵PA=AB,且N为PB的中点,∴AN⊥PB.
∵AD∩AN=A,∴PB⊥平面ADMN.
又∵PB?平面PBC,∴平面PBC⊥平面ADMN.
19. 【解析】(Ⅰ)依题意可设A、,则
, ,解得,. …………4分
即,又l过点P,易得AB方程为.………………6分
(Ⅱ)设圆的半径为R,则,其中d为弦心距,,可得,故所求圆的方程为.………………12分
20. 【解析】:(I)证明:连接, 在中,分别是的中点,所以, 又,所以,又平面ACD ,DC平面ACD, 所以平面ACD.
(Ⅱ)在中,,所以
而DC平面ABC,,所以平面ABC
而平面ABE, 所以平面ABE平面ABC, 所以平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以
所以平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是
在中, ,
所以.
21. 【解析】:(1)依题意,若年产量不足100台,另外投本false,固定投本600万,总收入150x万元,故利润false;若年产量不小于100台,另外投本false,固定投本600万,总收入150x万元,故利润false.
故false;
(2)当false时,false,在对称轴false处,取得最大值,false;
当false,false时,false,对勾函数false在false上递减,在false上递增,故false时,利润取得最大值,false,
综上可知,当年产量为110台时,该企业所获利润最大为3660万元.
22. 【解析】(1)证明:过点C作CM⊥AB,垂足为M,因为AD⊥DC,
所以四边形ADCM为矩形,所以AM=MB=2,
又AD=2,AB=4,所以AC=2,CM=2,BC=2,
所以AC2+BC2=AB2,所以AC⊥BC,因为AF⊥平面ABCD,AF∥BE,
所以BE⊥平面ABCD,所以BE⊥AC.
又BE?平面BCE,BC?平面BCE,且BE∩BC=B,
所以AC⊥平面BCE.
(2)因为AF⊥平面ABCD,所以AF⊥CM,
又CM⊥AB,AF?平面ABEF,
AB?平面ABEF,AF∩AB=A,所以CM⊥平面ABEF.
VE-BCF=VC-BEF=××BE×EF×CM=×2×4×2=.
(时间:120分钟,满分:150分)
选择题(本大题共12小题,每小题5分,共60分。给出的四个选项中,只有一项是符合题目要求的.)
1. 下列说法正确的是( )
A. 棱柱被平面分成的两部分可以都是棱柱
B. 底面是矩形的平行六面体是长方体
C. 棱柱底面一定是平行四边形
D. 棱锥的底面一定是三角形
2. 直线l1的倾斜角false,直线l1⊥l2,则直线l2的斜率为( )
A. -false B. false C. -false D. false
3. 如果AB>0,BC>0,那么直线Ax-By-C=0不经过的象限是( )
4343400205740A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 如图,AB是⊙O直径,C是圆周上不同于A、B的任意一点,PA与
平面ABC垂直,则四面体P_ABC的四个面中,直角三角形的个数有( )
A. 4个 B. 3个 C. 1个 D. 2个
5. 轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的( )
A. 4倍 B. 3倍 C. false 倍 D. 2倍
6. 已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:
①若m∥α,m∥β,则α∥β
②若m?α,n?α,m∥β,n∥β,则α∥β;
③m?α,n?β,m、n是异面直线,那么n与α相交;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β.
其中正确的命题是( )
A ①② B. ②③ C. ③④ D. ④
7. 某组合体的三视图如下,则它的体积是( )
3822065347345
357378058420
37572951083310俯视图
俯视图
A. false B. false C. false D. false
8. 点false关于直线false的对称点是( )
A. false B. false C. false D. false
9. 已知圆C与直线false及false都相切,圆心在直线false上,则圆C的方程为( )
A. false B. false
C. false D. false
10. 已知在四面体false中,false分别是false的中点,false,
则false与false所成角的度数为( )
A. false0 B. false0 C. false0 D. false0
402907549149011. 如图,在正三棱柱false中,false,若二面角false的大小为false,则点C到平面false的距离为( )
A. 1 B. false C. false D. false
12. 已知函数false若a,b,c互不相等,且false,则false的取值范围是( )
A.false B.false C.false D.false
填空题(本大题共4小题,每小题5分,共20分。答案填在答题卡对应题号后的横线上.)
直线false过点false且与以点false为端点的线段恒相交,则false的斜率取值范围是 .
14. 若两平行直线2x+y-4=0与y =-2x-k-2的距离不大于false,则实数k的取值范围是____.
15. 若直线l在x轴上的截距为1,点false到l的距离相等,则l的方程为_____.
16. 若三棱锥false中,false,其余各棱长均为5,则三棱锥内切球的表面积__.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
(1)false
(2)false
18. (本小题满分12分)
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,E为AD的中点,过A,D,N的平面交PC于点M. 求证: (1)EN∥平面PDC;
366712587630(2)BC⊥平面PEB;
(3)平面PBC⊥平面ADM
19.(本小题满分12分)
已知直线l过点P(1,1),并与直线l1:x-y+3=0和l2:2x+y-6=0分别交于点A、B,若线段AB被点P平分,求:
(1)直线l的方程;
(2)以坐标原点O为圆心且被l截得的弦长为false的圆的方程.
20. (本小题满分12分)
3600450417195如图,false平面false,false,false,false,false分别为false的中点.
(I)证明:false平面false;
(II)求false与平面false所成角的正弦值。
21.(本小题满分12分)
新能源开发能够有效地解决我国能源短缺和传统能源使用带来的环境污染问题,国家新能源政策的出台,给新能源产业带来了春天,已知某新能源企业,年固定成本600万,每生产false台设备,另需投入成本t万元,若年产量不足100台,则false;若年产量不小于100台,则false,每台设备售价150万元,通过市场分析,该企业生产的设备能全部售完.
(1)写出年利润y(万元)关于年产量x(台)的关系式;
(2)年产量为多少台时,该企业所获利润最大?
(本小题满分12分)
3276600758190如图,已知false平面false,四边形false为矩形,四边形false为直角梯形,false,AB∥CD,false,false.
(1)求证:false平面false;
(2)求三棱锥false的体积.
西华一高52届高一上期第七次周考数学参考答案(理科)
1.【答案】A【解析】对于B.底面是矩形的平行六面体,它的侧面不一定是矩形,故它也不一定是长方体,故B错;对于C.棱柱的底面是平面多边形,不一定是平行四边形,故C错;对于D.棱锥的底面是平面多边形,不一定是三角形,故D错;故选A.
2.【答案】C【解析】如图:直线L1的倾斜角α1=30°,直线L1⊥L2,则L2的倾斜角等于30°+90°=120°,∴L2的斜率为 tan120°=﹣tan60°false,故选C.
3.【答案】B【解析】:斜率为false,截距false,故不过第二象限.
4.【答案】A【解析】∵AB是圆O的直径,∴∠ACB=false,即false,三角形false是直角三角形.又∵false圆O所在的平面,∴三角形false和三角形false是直角三角形,且BC在此平面中,∴false平面false,∴三角形false是直角三角形.综上,三角形false,三角形false,三角形false,三角形false.直角三角形数量为4.故选:A.
5.【答案】D【解析】圆锥的轴截面是正三角形,设底面半径为r,则它的底面积为πr2;
圆锥的侧面积为:false2rπ?2r=2πr2;圆锥的侧面积是底面积的2倍.
6. 【答案】D【解析】①若m∥α,m∥β,则α∥β或α与β相交,错误命题;
②若m?α,n?α,m∥β,n∥β,则α∥β或α与β相交.错误的命题;
③m?α,n?β,m、n是异面直线,那么n与α相交,也可能n∥α,是错误命题;
④若α∩β=m,n∥m,且n?α,n?β,则n∥α且n∥β.是正确的命题.
7. 【答案】A【解析】:falsefalse,故选A.
8. 【答案】A【解析】设对称点为false,则false ,则false,故选A.
9. 【答案】B【解析】圆心在false上,圆心的纵横坐标值相反,显然能排除C、D;
验证:A中圆心false到两直线false的距离是false;
圆心false到直线false的距离是false.故A错误.
10. 【答案】A【解析】略
11. 【答案】C【解析】取false的中点false,连接false和false,根据二面角的定义,false.
由题意得false,所以false,false.
设false到平面false的距离为false,易知三棱锥false的体积三棱锥false的体积相等,
即false,解得false,故点C到平面false的距离为false.
12. 【答案】A【详解】作出函数false的图象如图所示:
令false,由图知:false,结合图象,不妨令false,以false,false,false ,false,false,false,所以false,
13.【解析】∵false
∴false
根据如下图形可知,
使直线false与线段false相交的斜率取值范围是false
14. 【答案】false
【解析】y=﹣2x﹣k﹣2的一般式方程为2x+y+k+2=0
则两平行直线的距离dfalse
得,|k+6|≤5,解得﹣11≤k≤﹣1,
当k+2=﹣4,即k=﹣6,此时两直线重合,
所以k的取值范围是false
15. 【答案】false或false
【解析】显然直线false轴时符合要求,此时false的方程为false.
当直线l的斜率存在时,设直线l的斜率为k,则l的方程为false,
即false.∵A,B到l的距离相等
∴false,∴false,∴false,
∴直线l的方程为false.故答案为false或false
16. 【答案】false
【解析】由题意得,易知内切球球心false到各面距离相等,
设false为false的中点,则false在false上且false为false的中点,
在false中,false,
所以三棱锥内切球的表面积为false.
17. 【解析】(1)false
falsefalse
falsefalse
(2)原式false
false.
18. 【解析】
(1)∵AD∥BC,BC?平面PBC,
AD?平面PBC,
∴AD∥平面PBC.又平面ADMN∩平面PBC=MN,∴AD∥MN.又∵AD∥BC,∴MN∥BC.
又∵N为PB的中点,∴M为PC的中点,
∴MN=falseBC.
∵E为AD的中点,DE=falseAD=falseBC=MN,
∴DEfalseMN,∴四边形DENM为平行四边形,
∴EN∥DM.又∵EN?平面PDC,DM?平面PDC,
∴EN∥平面PDC.
(2)∵四边形ABCD是边长为2的菱形,且∠BAD=60°,E为AD中点,
∴BE⊥AD.又∵PE⊥AD,PE∩BE=E,∴AD⊥平面PEB.∵AD∥BC,∴BC⊥平面PEB.
(3)由(2)知AD⊥PB.
又∵PA=AB,且N为PB的中点,∴AN⊥PB.
∵AD∩AN=A,∴PB⊥平面ADMN.
又∵PB?平面PBC,∴平面PBC⊥平面ADMN.
19. 【解析】(Ⅰ)依题意可设A、,则
, ,解得,. …………4分
即,又l过点P,易得AB方程为.………………6分
(Ⅱ)设圆的半径为R,则,其中d为弦心距,,可得,故所求圆的方程为.………………12分
20. 【解析】:(I)证明:连接, 在中,分别是的中点,所以, 又,所以,又平面ACD ,DC平面ACD, 所以平面ACD.
(Ⅱ)在中,,所以
而DC平面ABC,,所以平面ABC
而平面ABE, 所以平面ABE平面ABC, 所以平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以
所以平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是
在中, ,
所以.
21. 【解析】:(1)依题意,若年产量不足100台,另外投本false,固定投本600万,总收入150x万元,故利润false;若年产量不小于100台,另外投本false,固定投本600万,总收入150x万元,故利润false.
故false;
(2)当false时,false,在对称轴false处,取得最大值,false;
当false,false时,false,对勾函数false在false上递减,在false上递增,故false时,利润取得最大值,false,
综上可知,当年产量为110台时,该企业所获利润最大为3660万元.
22. 【解析】(1)证明:过点C作CM⊥AB,垂足为M,因为AD⊥DC,
所以四边形ADCM为矩形,所以AM=MB=2,
又AD=2,AB=4,所以AC=2,CM=2,BC=2,
所以AC2+BC2=AB2,所以AC⊥BC,因为AF⊥平面ABCD,AF∥BE,
所以BE⊥平面ABCD,所以BE⊥AC.
又BE?平面BCE,BC?平面BCE,且BE∩BC=B,
所以AC⊥平面BCE.
(2)因为AF⊥平面ABCD,所以AF⊥CM,
又CM⊥AB,AF?平面ABEF,
AB?平面ABEF,AF∩AB=A,所以CM⊥平面ABEF.
VE-BCF=VC-BEF=××BE×EF×CM=×2×4×2=.
同课章节目录
