(课时教案)北九下2.8二次函数与一元二次方程(1)
文档属性
| 名称 | (课时教案)北九下2.8二次函数与一元二次方程(1) |
|
|
| 格式 | zip | ||
| 文件大小 | 51.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-28 15:20:53 | ||
图片预览

文档简介
课题:二次函数与一元二次方程
教学过程分析
1.创设情境,激趣设疑
进球了吗?
在一场足球比赛中,有一名球员从球门正前方12m
处将球踢出射向球门,若球的飞行路线是一条抛物线,
如图所示.
(1)球的飞行高度(m)与水平距离(m)的
关系式是什么?
(2)若没有其他球员阴挡,足球能被射进球门吗?
你有几种求解方法?
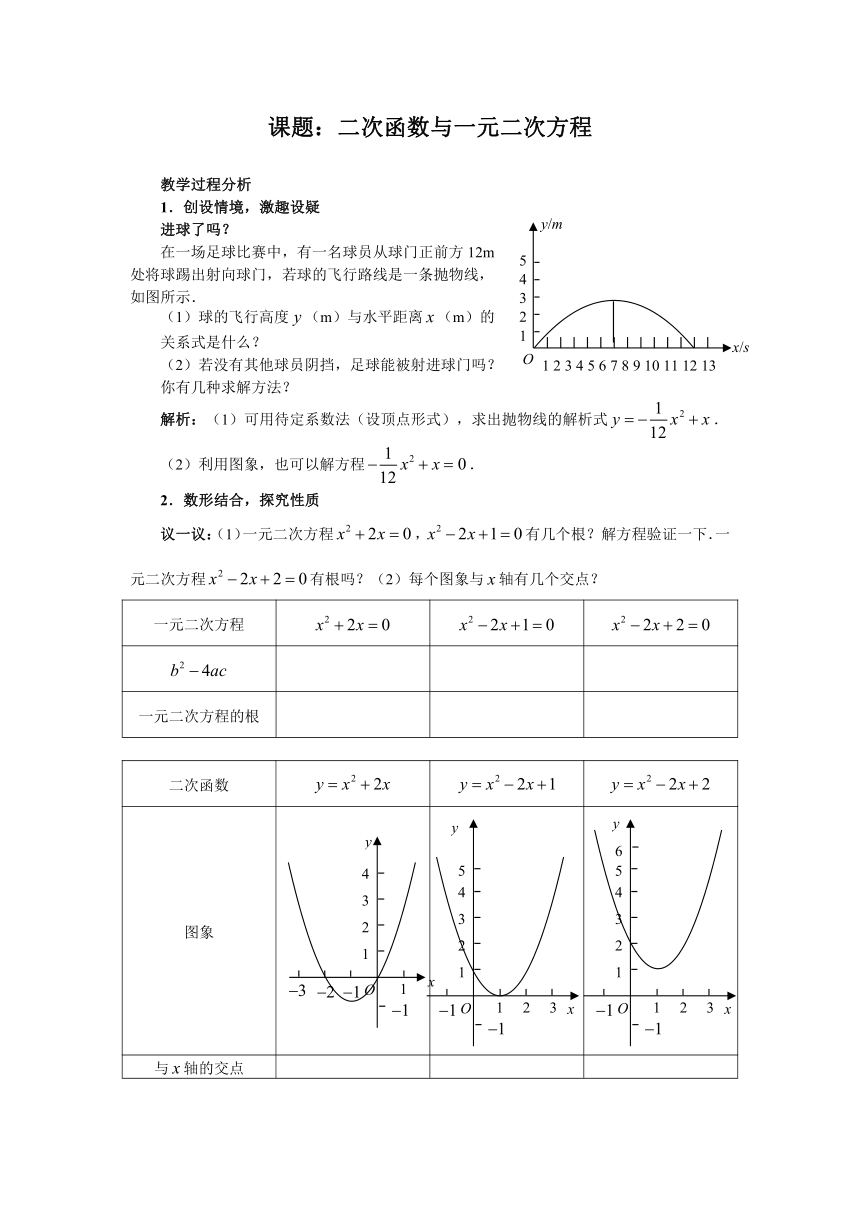
解析:(1)可用待定系数法(设顶点形式),求出抛物线的解析式.
(2)利用图象,也可以解方程.
2.数形结合,探究性质
议一议:(1)一元二次方程,有几个根?解方程验证一下.一元二次方程有根吗?(2)每个图象与轴有几个交点?
一元二次方程
一元二次方程的根
二次函数
图象
与轴的交点
问题:二次函数的图象和轴交点的坐标与一元二次方程的根有什么关系?
判别 一元二次方程() 二次函数()
与轴的交点坐标
3.引申思考,发散思维
球有多高:在一场足球比赛中,有一名球员从球门正前方12m处将球路踢出射向球门,球的飞行路线是一条抛物线,其解析式.
(1)球飞行的水平距离是多少时的高度是1.25m?
(2)球飞行的水平距离是多少时的高度是2m?
(3)球的高度能否达到4m
解析:(1)可利用图象,也可以解方程
(2)可利用图象,也可以解方程
(3),,无解.
归纳:二次函数()与直线有交点时,交点的横坐标即一元二次方程()的根.
4.实际应用,反馈释疑
水面有多宽:一座抛物线型拱桥如图所示,桥下面宽度
是4m时,拱高是2m,当水面下降1m后,水面宽度是
多少?(结果精确到0.1m)
解析:以抛物线的顶点为原点建立直角坐标系,使抛物线
的表达式为的形式.
喷泉中的数学:某广场喷泉喷出的水在空中经过的路线形成一条抛物线.它距地面的高度h(m)可用公式来表示,其中表示水从出水口喷出后经过的时间.
(1)作出函数的图象;
(2)当时,喷出的水距地面的高度分别是多少?
(3)方程,的根的实际意义分别是什么?你能在图象上表示出来吗?
解析:(1)如图
(2)当时,喷出的水距地面的高度是20m
(3)方程表示水离开地面及落地的时间;方程表示水距地面的高度为15m时的时间.
5.概括储存,导结新知
回顾与思考:你有哪些认识与体会?
师生行为:学生反思学习和解决问题的过程,发表见解,教师对学生的进步要给予肯定和鼓励.
口诀:
二次函数抛物线,交点问题图象见;
若给值取定值,解了方程立刻知.
作业布置:
1 2 3 4 5 6 7 8 9 10 11 12 13
5
4
3
2
1
O
x/s
y/m
O
x
y
1
1
2
2
3
3
4
5
O
x
y
1
1
2
3
4
O
x
y
1
1
2
2
3
3
4
5
6
1 2 3 4 5 6 7 8 9 10 11 12 13
5
4
3
2
1
O
x/s
y/m
1 2 3 4
20
15
10
5
O
t/s
h/m
教学过程分析
1.创设情境,激趣设疑
进球了吗?
在一场足球比赛中,有一名球员从球门正前方12m
处将球踢出射向球门,若球的飞行路线是一条抛物线,
如图所示.
(1)球的飞行高度(m)与水平距离(m)的
关系式是什么?
(2)若没有其他球员阴挡,足球能被射进球门吗?
你有几种求解方法?
解析:(1)可用待定系数法(设顶点形式),求出抛物线的解析式.
(2)利用图象,也可以解方程.
2.数形结合,探究性质
议一议:(1)一元二次方程,有几个根?解方程验证一下.一元二次方程有根吗?(2)每个图象与轴有几个交点?
一元二次方程
一元二次方程的根
二次函数
图象
与轴的交点
问题:二次函数的图象和轴交点的坐标与一元二次方程的根有什么关系?
判别 一元二次方程() 二次函数()
与轴的交点坐标
3.引申思考,发散思维
球有多高:在一场足球比赛中,有一名球员从球门正前方12m处将球路踢出射向球门,球的飞行路线是一条抛物线,其解析式.
(1)球飞行的水平距离是多少时的高度是1.25m?
(2)球飞行的水平距离是多少时的高度是2m?
(3)球的高度能否达到4m
解析:(1)可利用图象,也可以解方程
(2)可利用图象,也可以解方程
(3),,无解.
归纳:二次函数()与直线有交点时,交点的横坐标即一元二次方程()的根.
4.实际应用,反馈释疑
水面有多宽:一座抛物线型拱桥如图所示,桥下面宽度
是4m时,拱高是2m,当水面下降1m后,水面宽度是
多少?(结果精确到0.1m)
解析:以抛物线的顶点为原点建立直角坐标系,使抛物线
的表达式为的形式.
喷泉中的数学:某广场喷泉喷出的水在空中经过的路线形成一条抛物线.它距地面的高度h(m)可用公式来表示,其中表示水从出水口喷出后经过的时间.
(1)作出函数的图象;
(2)当时,喷出的水距地面的高度分别是多少?
(3)方程,的根的实际意义分别是什么?你能在图象上表示出来吗?
解析:(1)如图
(2)当时,喷出的水距地面的高度是20m
(3)方程表示水离开地面及落地的时间;方程表示水距地面的高度为15m时的时间.
5.概括储存,导结新知
回顾与思考:你有哪些认识与体会?
师生行为:学生反思学习和解决问题的过程,发表见解,教师对学生的进步要给予肯定和鼓励.
口诀:
二次函数抛物线,交点问题图象见;
若给值取定值,解了方程立刻知.
作业布置:
1 2 3 4 5 6 7 8 9 10 11 12 13
5
4
3
2
1
O
x/s
y/m
O
x
y
1
1
2
2
3
3
4
5
O
x
y
1
1
2
3
4
O
x
y
1
1
2
2
3
3
4
5
6
1 2 3 4 5 6 7 8 9 10 11 12 13
5
4
3
2
1
O
x/s
y/m
1 2 3 4
20
15
10
5
O
t/s
h/m
