四种命题
图片预览








文档简介
(共22张PPT)
33.四种命题
(1)什么是命题?命题是由哪几部分构成的?
一般地,我们把用语言,符号,式子表述的,能够判断真假的语句叫做命题
一般地,一个命题有条件和结论两部分组成,因此命题可以表述为“如果.....那么...” 数学中记为“若p则q”,其中p是命题的条件,q是命题的结论
一.问题情境:
下面四个命题:
(1)如果两个三角形全等, 那么它们的面积相等.
(2)如果两个三角形的面积相等, 那么它们全等.
(3如果两个三角形不全等, 那么它们的面积不相等.
(4)如果两个三角形的面积不相等, 那么它们不全等.
命题(2)(3)(4)与命题(1)有何关系
2、互否命题:如果第一个命题的条件和结论是第二个命题的条件和结论的否定,那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的否命题。
3、互为逆否命题:如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定,那么这两个命题叫做互为逆否命题。
1、互逆命题:如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。
三个
概念
1. 交换原命题的条件和结论,所得命题是原命题的逆命题.
2. 同时否定原命题的条件和结论,所得命题是原命题的否命题.
3. 交换原命题的条件和结论,并且同时否定,所得的命题是原命题的逆否命题.
命题P的否定,记作“ P”。读作“非P”。
一个
符号
互否
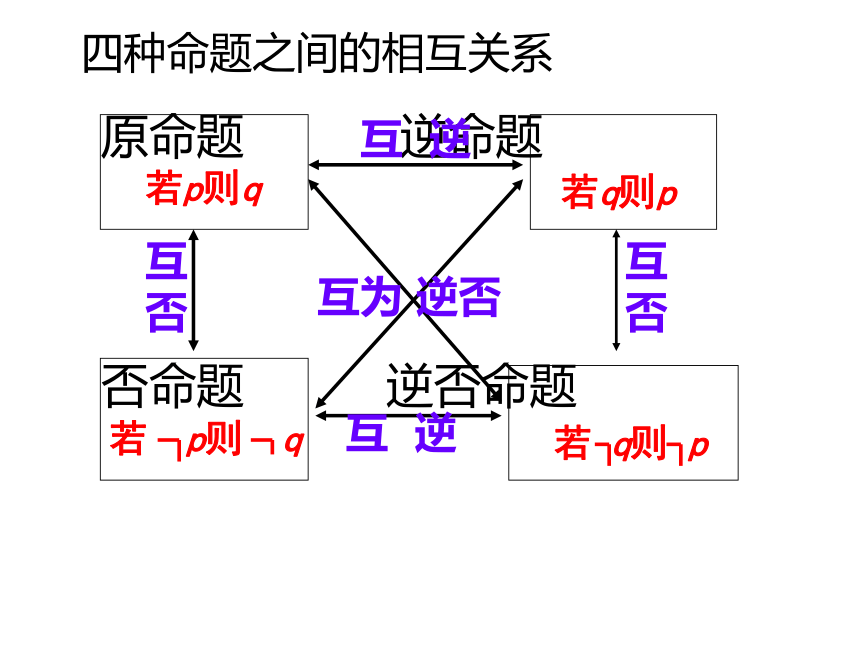
四种命题之间的相互关系
原命题 逆命题
否命题 逆否命题
若p则q
互 逆
互 逆
互否
互为 逆否
若 p则 q
若 q则 p
若q则p
四.数学运用
例1.写出命题“若a=0 , 则ab=0”的逆命题, 否命题与逆否命题, 并指出四个命题的真假.
原命题:若a=0, 则ab=0。
逆命题:若ab=0, 则a=0。
否命题:若a≠ 0, 则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
想一想?
(2)若其逆命题为真,则其否命题一定为真。
但其原命题、逆否命题不一定为真。
由以上三例及总结我们能发现什么?
即:原命题与逆否命题的真假是等价的。
逆命题与否命题的真假是等价的。
(1)原命题为真,则其逆否命题一定为真。
但其逆命题、否命题不一定为真。
总结:
练一练
1.判断下列说法是否正确。
1)一个命题的逆命题为真,它的逆否命题不一定为真;
(对)
2)一个命题的否命题为真,它的逆命题一定为真。
(对)
2.四种命题真命题的个数可能为( )个。
答:0个、2个、4个。
3)一个命题的原命题为假,它的逆命题一定为假。
(错)
4)一个命题的逆否命题为假,它的否命题为假。
(错)
变题写出命题“若 x +y =0,则x=0且y=0”的逆命题,否命题,逆否命题.
2
2
变1:写出命题“若 x +y =0,则x=0且y=0”的逆命题,否命题,逆否命题.
2
2
逆命题:若x=0且y=0,则x +y =0
2
2
否命题:若 x +y = 0,则 x=0或y=0
2
2
逆否命题:若x=0或y=0,则x +y =0
2
2
提示:
“或”的否定是“且”,“且”的否定是“或”
变2:设原命题是:当c>0时,若a>b,则ac>bc.
写出它的逆命题、否命题、逆否命题。
并分别判断它们的真假。
解:逆命题:当c>0时,若ac>bc, 则a>b.
否命题:当c>0时,若a≤b, 则ac≤bc.
逆否命题:当c>0时,若ac≤bc, 则a≤b.
(真)
(真)
(真)
分析:“当c>0时”是大前提,写其它命题时应该保留。
原命题的条件是“a>b”,
结论是“ac>bc”。
例2.把下列命题改写成“若p则q”的形式, 并写出它的逆命题, 否命题与逆否命题, 同时指出它们的真假.
(1)对顶角相等;
(2)全等三角形的对应边相等;
(3)四条边相等的四边形是正方形;
(4)实数的平方是非负数.
(5)已知a、b、c、d是实数,若a=b, c=d,则a+c=b+d .
若两个角是对顶角,则这两个角相等。
例2.(1)对顶角相等;
(2)全等三角形的对应边相等;
(3)四条边相等的四边形是正方形;
(4)实数的平方是非负数.
(5)已知a、b、c、d是实数,若a=b, c=d,则a+c=b+d .
原命题:若两个角是对顶角,则这两个角相等。
原命题:若两个三角形是全等三角形,则这两个三角形对应边相等.
原命题:若一个四边形的四条边相等,则它是正方形。
原命题:若一个数是实数的平方,则它是非负数。
原命题:已知a、b、c、d是实数,若a=b, c=d,
则a+c=b+d .
例2.(1)对顶角相等;
(2)全等三角形的对应边相等;
原命题:若两个角是对顶角,则这两个角相等。
原命题:若两个三角形是全等三角形,则它们对应边相等。
逆命题:若两个角相等,则它们是对顶角。
否命题:若两个角不是对顶角,则它们不相等。
逆否命题:若两个角不相等,则它们不是对顶角。
否命题:若两个三角形不是全等三角形,则它们的对应边不全相等。
逆命题:若两个三角形对应边相等,则它们是全等三角形。
逆否命题:若两个三角形的对应边不全相等,则它们不是全等三角形。
结论1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则Q”的形式)
结论2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。
注意:三种命题中最难写 的是否命题。
例2(3)四条边相等的四边形是正方形;
(4)实数的平方是非负数.
原命题:若一个四边形的四条边相等,则它是正方形。
原命题:若一个数是实数的平方,则它是非负数。
逆命题:若一个四边形是正方形,则它的四条边相等。
否命题:若一个四边形的四条边不全相等,则它不是正方形。
逆否命题:若一个四边形不是正方形,则它的四条边不全相等。
逆命题:若一个数是非负数,则它是实数的平方。
否命题:若一个数不是实数的平方,则它不是非负数。
逆否命题:若一个数不是非负数,则它不是实数的平方。
例2 (5)已知a、b、c、d是实数,若a=b,
c=d,则a+c=b+d .
原命题:已知a、b、c、d是实数,若a=b, c=d,则a+c=b+d .
逆命题:已知a、b、c、d是实数,若a+c=b+d ,则a=b, c=d.
否命题:已知a、b、c、d是实数,若a ≠ b, c ≠ d,则a+c ≠ b+d .
逆否命题:已知a、b、c、d是实数,若 a+c ≠ b+d ,则a ≠ b, c ≠ d.
例2 (6)若xy=6,则x=3且y=2.
原命题:若xy=6,则x=3且y=2.
逆命题:若x=3且y=2 ,则xy=6.
否命题:若xy ≠ 6,则x ≠ 3或y ≠ 2.
逆否命题:若 x ≠ 3或y ≠ 2 ,则xy ≠ 6.
若一个整数的末位是0,则它可以被5整除。
若一个点在线段的垂直平分线上,则它到这条线段两端点的距离相等。
若一条直线到圆心的距离不等于半径,则它不是圆的切线。
练习 1、把下列命题改写成“若P则Q”的形式“: (1)末位是0的整数,可以被5整除;
(2)线段的垂直平分线上的点与这条线段两端点的距离相等;
(3)到圆心的距离不等于半径的直线不是圆的切线;
小结:
(1) 写命题的逆命题、否命题、逆否命题的方法.
(2) 四种命题的真假关系
33.四种命题
(1)什么是命题?命题是由哪几部分构成的?
一般地,我们把用语言,符号,式子表述的,能够判断真假的语句叫做命题
一般地,一个命题有条件和结论两部分组成,因此命题可以表述为“如果.....那么...” 数学中记为“若p则q”,其中p是命题的条件,q是命题的结论
一.问题情境:
下面四个命题:
(1)如果两个三角形全等, 那么它们的面积相等.
(2)如果两个三角形的面积相等, 那么它们全等.
(3如果两个三角形不全等, 那么它们的面积不相等.
(4)如果两个三角形的面积不相等, 那么它们不全等.
命题(2)(3)(4)与命题(1)有何关系
2、互否命题:如果第一个命题的条件和结论是第二个命题的条件和结论的否定,那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的否命题。
3、互为逆否命题:如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定,那么这两个命题叫做互为逆否命题。
1、互逆命题:如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。
三个
概念
1. 交换原命题的条件和结论,所得命题是原命题的逆命题.
2. 同时否定原命题的条件和结论,所得命题是原命题的否命题.
3. 交换原命题的条件和结论,并且同时否定,所得的命题是原命题的逆否命题.
命题P的否定,记作“ P”。读作“非P”。
一个
符号
互否
四种命题之间的相互关系
原命题 逆命题
否命题 逆否命题
若p则q
互 逆
互 逆
互否
互为 逆否
若 p则 q
若 q则 p
若q则p
四.数学运用
例1.写出命题“若a=0 , 则ab=0”的逆命题, 否命题与逆否命题, 并指出四个命题的真假.
原命题:若a=0, 则ab=0。
逆命题:若ab=0, 则a=0。
否命题:若a≠ 0, 则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
想一想?
(2)若其逆命题为真,则其否命题一定为真。
但其原命题、逆否命题不一定为真。
由以上三例及总结我们能发现什么?
即:原命题与逆否命题的真假是等价的。
逆命题与否命题的真假是等价的。
(1)原命题为真,则其逆否命题一定为真。
但其逆命题、否命题不一定为真。
总结:
练一练
1.判断下列说法是否正确。
1)一个命题的逆命题为真,它的逆否命题不一定为真;
(对)
2)一个命题的否命题为真,它的逆命题一定为真。
(对)
2.四种命题真命题的个数可能为( )个。
答:0个、2个、4个。
3)一个命题的原命题为假,它的逆命题一定为假。
(错)
4)一个命题的逆否命题为假,它的否命题为假。
(错)
变题写出命题“若 x +y =0,则x=0且y=0”的逆命题,否命题,逆否命题.
2
2
变1:写出命题“若 x +y =0,则x=0且y=0”的逆命题,否命题,逆否命题.
2
2
逆命题:若x=0且y=0,则x +y =0
2
2
否命题:若 x +y = 0,则 x=0或y=0
2
2
逆否命题:若x=0或y=0,则x +y =0
2
2
提示:
“或”的否定是“且”,“且”的否定是“或”
变2:设原命题是:当c>0时,若a>b,则ac>bc.
写出它的逆命题、否命题、逆否命题。
并分别判断它们的真假。
解:逆命题:当c>0时,若ac>bc, 则a>b.
否命题:当c>0时,若a≤b, 则ac≤bc.
逆否命题:当c>0时,若ac≤bc, 则a≤b.
(真)
(真)
(真)
分析:“当c>0时”是大前提,写其它命题时应该保留。
原命题的条件是“a>b”,
结论是“ac>bc”。
例2.把下列命题改写成“若p则q”的形式, 并写出它的逆命题, 否命题与逆否命题, 同时指出它们的真假.
(1)对顶角相等;
(2)全等三角形的对应边相等;
(3)四条边相等的四边形是正方形;
(4)实数的平方是非负数.
(5)已知a、b、c、d是实数,若a=b, c=d,则a+c=b+d .
若两个角是对顶角,则这两个角相等。
例2.(1)对顶角相等;
(2)全等三角形的对应边相等;
(3)四条边相等的四边形是正方形;
(4)实数的平方是非负数.
(5)已知a、b、c、d是实数,若a=b, c=d,则a+c=b+d .
原命题:若两个角是对顶角,则这两个角相等。
原命题:若两个三角形是全等三角形,则这两个三角形对应边相等.
原命题:若一个四边形的四条边相等,则它是正方形。
原命题:若一个数是实数的平方,则它是非负数。
原命题:已知a、b、c、d是实数,若a=b, c=d,
则a+c=b+d .
例2.(1)对顶角相等;
(2)全等三角形的对应边相等;
原命题:若两个角是对顶角,则这两个角相等。
原命题:若两个三角形是全等三角形,则它们对应边相等。
逆命题:若两个角相等,则它们是对顶角。
否命题:若两个角不是对顶角,则它们不相等。
逆否命题:若两个角不相等,则它们不是对顶角。
否命题:若两个三角形不是全等三角形,则它们的对应边不全相等。
逆命题:若两个三角形对应边相等,则它们是全等三角形。
逆否命题:若两个三角形的对应边不全相等,则它们不是全等三角形。
结论1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则Q”的形式)
结论2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。
注意:三种命题中最难写 的是否命题。
例2(3)四条边相等的四边形是正方形;
(4)实数的平方是非负数.
原命题:若一个四边形的四条边相等,则它是正方形。
原命题:若一个数是实数的平方,则它是非负数。
逆命题:若一个四边形是正方形,则它的四条边相等。
否命题:若一个四边形的四条边不全相等,则它不是正方形。
逆否命题:若一个四边形不是正方形,则它的四条边不全相等。
逆命题:若一个数是非负数,则它是实数的平方。
否命题:若一个数不是实数的平方,则它不是非负数。
逆否命题:若一个数不是非负数,则它不是实数的平方。
例2 (5)已知a、b、c、d是实数,若a=b,
c=d,则a+c=b+d .
原命题:已知a、b、c、d是实数,若a=b, c=d,则a+c=b+d .
逆命题:已知a、b、c、d是实数,若a+c=b+d ,则a=b, c=d.
否命题:已知a、b、c、d是实数,若a ≠ b, c ≠ d,则a+c ≠ b+d .
逆否命题:已知a、b、c、d是实数,若 a+c ≠ b+d ,则a ≠ b, c ≠ d.
例2 (6)若xy=6,则x=3且y=2.
原命题:若xy=6,则x=3且y=2.
逆命题:若x=3且y=2 ,则xy=6.
否命题:若xy ≠ 6,则x ≠ 3或y ≠ 2.
逆否命题:若 x ≠ 3或y ≠ 2 ,则xy ≠ 6.
若一个整数的末位是0,则它可以被5整除。
若一个点在线段的垂直平分线上,则它到这条线段两端点的距离相等。
若一条直线到圆心的距离不等于半径,则它不是圆的切线。
练习 1、把下列命题改写成“若P则Q”的形式“: (1)末位是0的整数,可以被5整除;
(2)线段的垂直平分线上的点与这条线段两端点的距离相等;
(3)到圆心的距离不等于半径的直线不是圆的切线;
小结:
(1) 写命题的逆命题、否命题、逆否命题的方法.
(2) 四种命题的真假关系
