充分条件和必要条件(1)
图片预览






文档简介
(共16张PPT)
复习回顾:
1.命题的定义和结构:
2.四种命题的定义及其相互关系:
1.判断语句是否是命题:
一.基础知识:
二.题型与方法:
-------定义法:关键是能否判断真假
2.改写命题结构为“若p则q”形式
-------关键找条件与结论
互否
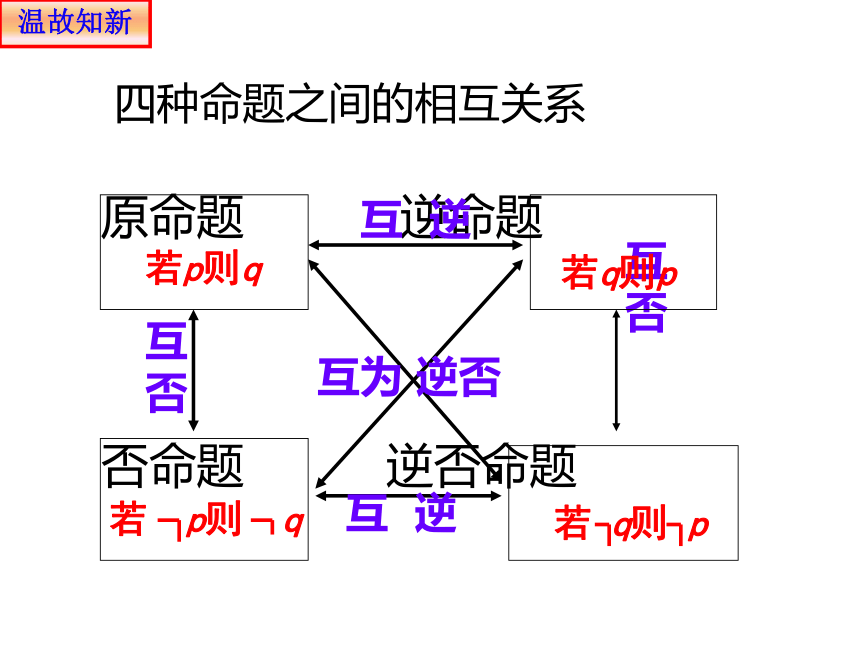
四种命题之间的相互关系
原命题 逆命题
否命题 逆否命题
若p则q
互 逆
互 逆
互否
互为 逆否
若 p则 q
若 q则 p
若q则p
温故知新
注:互为逆否的命题是等价命题;它们同真同假.
3.写出四种命题并判断真假
-------关键找条件与结论;注意否命题与命题的否定的区别.
充分条件和必要条件
判断下列命题的真假
1.若x=y,则x2=y2
真命题
2.若x2>1,则x>1
记作:x=y x2=y2
记作:x2>1 x>1
假命题
一般地,“若p则q”为真,记为p q;
“若p则q”为假,记为p q;
1.充分条件和必要条件的定义:
如果 ,
那么称p是q的充分条件,同时称q是p的必要条件.
1.充分条件和必要条件的定义:
如果 ,
那么称p是q的充分条件,同时称q是p的必要条件.
2.p、q关系的分类:
分类
充分条件
必要条件
充分必要条件
充分不必要条件
必要不充分条件
既不充分又不必要条件
必要条件
充分条件
充分必要条件
必要不充分条件
充分不必要条件
既不充分又不必要条件
p是q的什么条件
q是p的什么条件
例1.指出下列各题中, p是q的什么条件
(1)p: x-1=0 , q: (x-1)(x+2)=0 .
(2)p: 两直线平行, q: 内错角相等.
(3)p: a>b, q: a2>b2 .
(4)p: 四边形的四条边相等, q: 四边形是正方形.
(5)p: 两直线垂直, q: 两直线的斜率之积为-1 .
(6)p: lga>lgb , q: a>b .
(1)p: x-1≠0 ;q: (x-1)(x+2)≠0。
练习:指出p是q的什么条件?
(2)p:x>5 q:x≥5 ;
充要条件的集合思想
设P={p}, Q={q},
①若P Q ,则p是q的充分但不必要条件,
而q是p的必要但不充分条件.
②若P=Q,则p是q的充要条件(q也是p的充要条件).
③若P Q且Q P ,则p是q的既不充分也不必要条件.
若 q是 p的必要而非充分条件,求实数m的取值范围.
分析:先写出“ p”和“ q”,
然后由“ q” “ p”,但“ p” “ q”,求实数m的取值范围.
注意利用元素的特性,并结合数轴观察.
解 由x2-2x+1-m2≤0,得1-m≤x≤1+m(m>0).
所以“ q”:A={x∈R|x>1+m或x<1-m,m>0}
所以“ p”:B={x∈R|x>10或x<-2}.
由“ p”是“ q”的充分而不必要条件:知A B.
解得 0<m≤3为所求.
思考:若 q是 p的充分而非必要条件呢?如何求实数m的取值范围?
小结:条件关系的判断
1.方法
2.步骤
⑴分清条件和结论;
⑵研究双向关系;
⑶结论。
3.正难则反
——定义法
例2.已知p、q都是r的必要条件, S是r的充分条件, q是S的充分条件, 那么.
(1)S是q的什么条件 (2) r是q的什么条件 (3) p是q的什么条件
小结:1.图示分析法;
2.传递性:
3.循环性:
练2.已知p是q的充分条件, q是r的充分条件,r是p的充分条件,则p是r的 条件.
练1.已知p是q的充分条件, q是r的充分条件,则p是r的 条件.
练3.已知p是q的充分不必要条件, q是r的充分不必要条件,则p是r的 条件.
充分不必要
充分
充要
课堂小结:
1.条件关系的定义、分类;
2.条件关系的判断。
复习回顾:
1.命题的定义和结构:
2.四种命题的定义及其相互关系:
1.判断语句是否是命题:
一.基础知识:
二.题型与方法:
-------定义法:关键是能否判断真假
2.改写命题结构为“若p则q”形式
-------关键找条件与结论
互否
四种命题之间的相互关系
原命题 逆命题
否命题 逆否命题
若p则q
互 逆
互 逆
互否
互为 逆否
若 p则 q
若 q则 p
若q则p
温故知新
注:互为逆否的命题是等价命题;它们同真同假.
3.写出四种命题并判断真假
-------关键找条件与结论;注意否命题与命题的否定的区别.
充分条件和必要条件
判断下列命题的真假
1.若x=y,则x2=y2
真命题
2.若x2>1,则x>1
记作:x=y x2=y2
记作:x2>1 x>1
假命题
一般地,“若p则q”为真,记为p q;
“若p则q”为假,记为p q;
1.充分条件和必要条件的定义:
如果 ,
那么称p是q的充分条件,同时称q是p的必要条件.
1.充分条件和必要条件的定义:
如果 ,
那么称p是q的充分条件,同时称q是p的必要条件.
2.p、q关系的分类:
分类
充分条件
必要条件
充分必要条件
充分不必要条件
必要不充分条件
既不充分又不必要条件
必要条件
充分条件
充分必要条件
必要不充分条件
充分不必要条件
既不充分又不必要条件
p是q的什么条件
q是p的什么条件
例1.指出下列各题中, p是q的什么条件
(1)p: x-1=0 , q: (x-1)(x+2)=0 .
(2)p: 两直线平行, q: 内错角相等.
(3)p: a>b, q: a2>b2 .
(4)p: 四边形的四条边相等, q: 四边形是正方形.
(5)p: 两直线垂直, q: 两直线的斜率之积为-1 .
(6)p: lga>lgb , q: a>b .
(1)p: x-1≠0 ;q: (x-1)(x+2)≠0。
练习:指出p是q的什么条件?
(2)p:x>5 q:x≥5 ;
充要条件的集合思想
设P={p}, Q={q},
①若P Q ,则p是q的充分但不必要条件,
而q是p的必要但不充分条件.
②若P=Q,则p是q的充要条件(q也是p的充要条件).
③若P Q且Q P ,则p是q的既不充分也不必要条件.
若 q是 p的必要而非充分条件,求实数m的取值范围.
分析:先写出“ p”和“ q”,
然后由“ q” “ p”,但“ p” “ q”,求实数m的取值范围.
注意利用元素的特性,并结合数轴观察.
解 由x2-2x+1-m2≤0,得1-m≤x≤1+m(m>0).
所以“ q”:A={x∈R|x>1+m或x<1-m,m>0}
所以“ p”:B={x∈R|x>10或x<-2}.
由“ p”是“ q”的充分而不必要条件:知A B.
解得 0<m≤3为所求.
思考:若 q是 p的充分而非必要条件呢?如何求实数m的取值范围?
小结:条件关系的判断
1.方法
2.步骤
⑴分清条件和结论;
⑵研究双向关系;
⑶结论。
3.正难则反
——定义法
例2.已知p、q都是r的必要条件, S是r的充分条件, q是S的充分条件, 那么.
(1)S是q的什么条件 (2) r是q的什么条件 (3) p是q的什么条件
小结:1.图示分析法;
2.传递性:
3.循环性:
练2.已知p是q的充分条件, q是r的充分条件,r是p的充分条件,则p是r的 条件.
练1.已知p是q的充分条件, q是r的充分条件,则p是r的 条件.
练3.已知p是q的充分不必要条件, q是r的充分不必要条件,则p是r的 条件.
充分不必要
充分
充要
课堂小结:
1.条件关系的定义、分类;
2.条件关系的判断。
