1.1.1 平均变化率
图片预览





文档简介
(共27张PPT)
1.1平均变化率
第一次:1997年4月1日,最高时速140公里
第二次:1998年10月1日,最高时速160公里
第三次:2000年10月21日,重点是亚欧大陆桥陇海、兰新线、京九线和浙赣线
第四次:2001年11月21日,实施新列车运行图,全国铁路实行联网售票
第五次:2004年4月18日,最高时速200公里
第六次:2007年4月18日,最高时速250公里
八达岭
井冈山
西岳华山
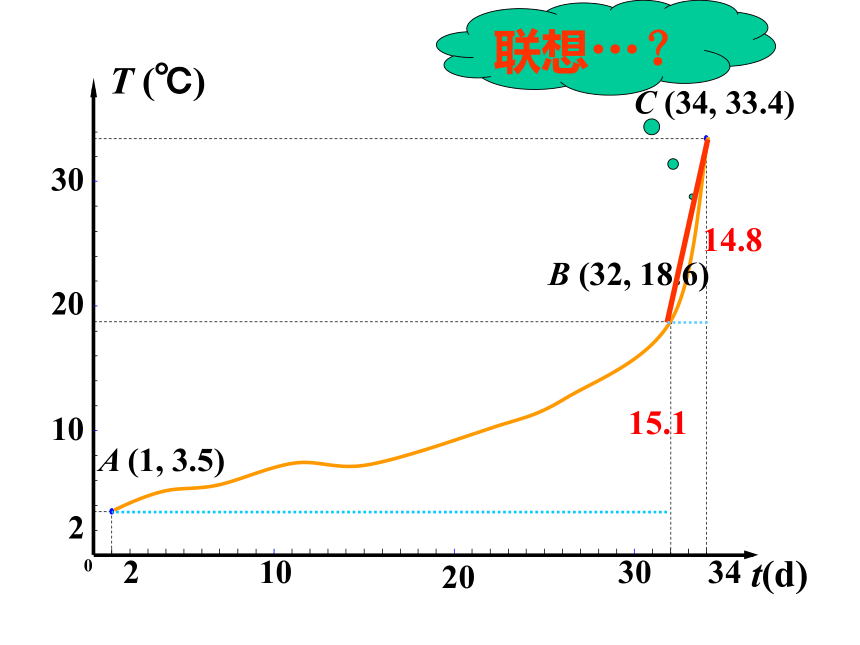
时间 3月18日 4月18日 4月20日
日最高气温 3.5℃ 18.6℃ 33.4℃
温差15.1℃
温差14.8℃
t(d)
20
30
34
2
10
20
30
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
t(d)
20
30
34
2
10
20
30
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
联想…?
14.8
15.1
1、平均变化率
一般的,函数f(x)在区间[x1,x2]
的平均变化率为
t(d)
20
30
34
2
10
20
30
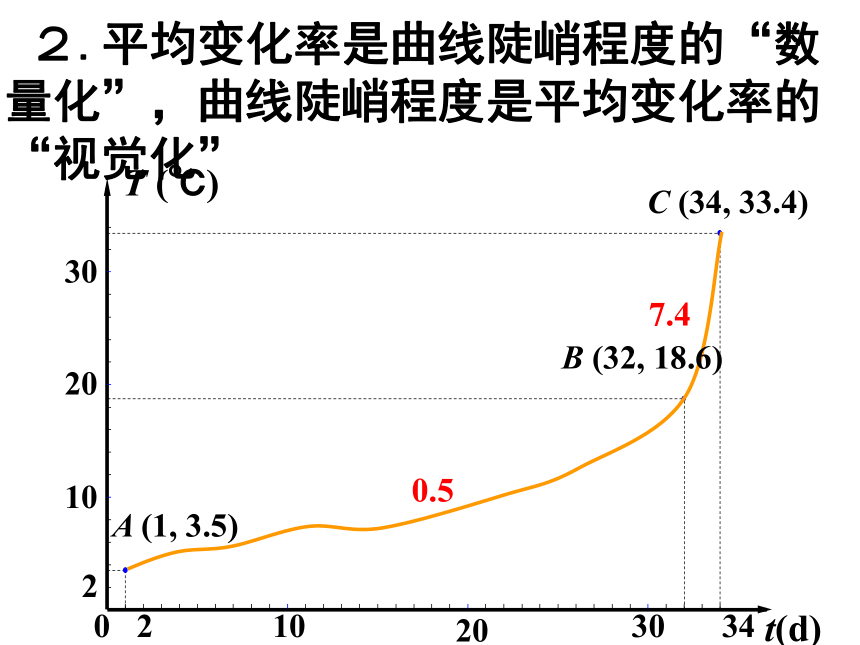
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
7.4
0.5
2.平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“视觉化”
在经营某商品中,甲 挣到10万元,乙 挣到6万元,如何比较和评价甲、乙两人的经营成果?
用5年时间
用2年时间
牛刀小试
同学们,你们能举一些生活中的例子吗
例1 (1)某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.
T(月)
W(kg)
6
3
9
12
3.5
6.5
8.6
11
数学应用
0
例1.(2)水经过虹吸管从容器甲中流向容器乙,ts后容器甲中水的体积V(t)=5×e-0.1t(单位:cm3),计算第一个10s内V的平均变化率(精确到0.0001)
思考:是否表示10s内每一时刻容器甲中水的体积V减少的速度
甲
乙
解:在区间[0,10]内的平均变化率为:
例2 (1)已知函数f(x)=2x+1,g(x)=-2x,分别计算在区间[-3,-1],[0,5]上f(x)及g(x)的平均变化率。
同学们发现了什么 !
一次函数y=kx+b在区间[m,n]上的平均变化率就等于k,和区间中的m,n无关.
已知函数f(x)=3x+1,分别计算f(x) 在下列区间上的平均变化率:
(1)[-1,2];
(2)[-1,1];
(3)[-1,-0.9].
3
3
3
大显身手
例2(2)已知函数f(x)=x2,分别计算f(x)在下列区间上的平均变化率:
①[1,3];
②[1,2];
③[1,1.1]
④[1,1.001]
4
3
2.1
2.001
小结:通过计算发现函数f(x)=x2的平均变化率随x2-x1无限变小而无限接近常数.
越来越小
趋近于
2
C
x
1
2
3
o
1
4
9
y
A
B
已知函数f(x)=ax2,在区间[1,2]上的平均变化率为 ,则f(x)在区间[-2,-1]上的平均变化率为_______
[变式]
1.已知函数 ,分别计算f(x)在下列区 间上的平均变化率:
(1)[1,2];(2)[1,1.5];(3)[1,1.1].
反馈练习
2.计算正弦函数y=sinx在区间 和
上的平均变化率,并比较大小
蓦然回首
这节课我的收获是什么?
归纳小结:
1 .平均变化率的概念:
3 .用平均变化率近似地量化曲线在某区间上的 “陡峭”
程度.
曲线越“陡峭”,说明变量变化
越快;
越慢.
曲线越“平缓”,说明变量变化
2.平均变化率的几何意义:
过曲线上A、B两点的直线的斜率.
f(x2)-f(x1)
x2-x1
x
y
o
函数
在区间 上的平均变化率为
一般地,
只有微分学才能使自然科学有可能用数学来不仅仅表明状态,而且也表明过程:运动
恩格斯
作 业
感受理解:课本第7页练习4
思考运用:课本第16页习题11(1)
探究拓展:课本第16页习题12(1)(2)
1.1平均变化率
第一次:1997年4月1日,最高时速140公里
第二次:1998年10月1日,最高时速160公里
第三次:2000年10月21日,重点是亚欧大陆桥陇海、兰新线、京九线和浙赣线
第四次:2001年11月21日,实施新列车运行图,全国铁路实行联网售票
第五次:2004年4月18日,最高时速200公里
第六次:2007年4月18日,最高时速250公里
八达岭
井冈山
西岳华山
时间 3月18日 4月18日 4月20日
日最高气温 3.5℃ 18.6℃ 33.4℃
温差15.1℃
温差14.8℃
t(d)
20
30
34
2
10
20
30
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
t(d)
20
30
34
2
10
20
30
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
联想…?
14.8
15.1
1、平均变化率
一般的,函数f(x)在区间[x1,x2]
的平均变化率为
t(d)
20
30
34
2
10
20
30
A (1, 3.5)
B (32, 18.6)
0
C (34, 33.4)
T (℃)
2
10
7.4
0.5
2.平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“视觉化”
在经营某商品中,甲 挣到10万元,乙 挣到6万元,如何比较和评价甲、乙两人的经营成果?
用5年时间
用2年时间
牛刀小试
同学们,你们能举一些生活中的例子吗
例1 (1)某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.
T(月)
W(kg)
6
3
9
12
3.5
6.5
8.6
11
数学应用
0
例1.(2)水经过虹吸管从容器甲中流向容器乙,ts后容器甲中水的体积V(t)=5×e-0.1t(单位:cm3),计算第一个10s内V的平均变化率(精确到0.0001)
思考:是否表示10s内每一时刻容器甲中水的体积V减少的速度
甲
乙
解:在区间[0,10]内的平均变化率为:
例2 (1)已知函数f(x)=2x+1,g(x)=-2x,分别计算在区间[-3,-1],[0,5]上f(x)及g(x)的平均变化率。
同学们发现了什么 !
一次函数y=kx+b在区间[m,n]上的平均变化率就等于k,和区间中的m,n无关.
已知函数f(x)=3x+1,分别计算f(x) 在下列区间上的平均变化率:
(1)[-1,2];
(2)[-1,1];
(3)[-1,-0.9].
3
3
3
大显身手
例2(2)已知函数f(x)=x2,分别计算f(x)在下列区间上的平均变化率:
①[1,3];
②[1,2];
③[1,1.1]
④[1,1.001]
4
3
2.1
2.001
小结:通过计算发现函数f(x)=x2的平均变化率随x2-x1无限变小而无限接近常数.
越来越小
趋近于
2
C
x
1
2
3
o
1
4
9
y
A
B
已知函数f(x)=ax2,在区间[1,2]上的平均变化率为 ,则f(x)在区间[-2,-1]上的平均变化率为_______
[变式]
1.已知函数 ,分别计算f(x)在下列区 间上的平均变化率:
(1)[1,2];(2)[1,1.5];(3)[1,1.1].
反馈练习
2.计算正弦函数y=sinx在区间 和
上的平均变化率,并比较大小
蓦然回首
这节课我的收获是什么?
归纳小结:
1 .平均变化率的概念:
3 .用平均变化率近似地量化曲线在某区间上的 “陡峭”
程度.
曲线越“陡峭”,说明变量变化
越快;
越慢.
曲线越“平缓”,说明变量变化
2.平均变化率的几何意义:
过曲线上A、B两点的直线的斜率.
f(x2)-f(x1)
x2-x1
x
y
o
函数
在区间 上的平均变化率为
一般地,
只有微分学才能使自然科学有可能用数学来不仅仅表明状态,而且也表明过程:运动
恩格斯
作 业
感受理解:课本第7页练习4
思考运用:课本第16页习题11(1)
探究拓展:课本第16页习题12(1)(2)
