1.1.2(1)曲线上一点处的切线
图片预览





文档简介
(共17张PPT)
曲线上一点处的切线
平均变化率
一般的,函数 在区间上 的平均变化率为
复均变化率近似地刻画了曲线在某一区间上的变化趋势.
·
P
问题:如何精确地刻画曲线在某一点处的变化趋势呢
直线l的斜率便量化了曲线经过点P时上升或下降的变化趋势.
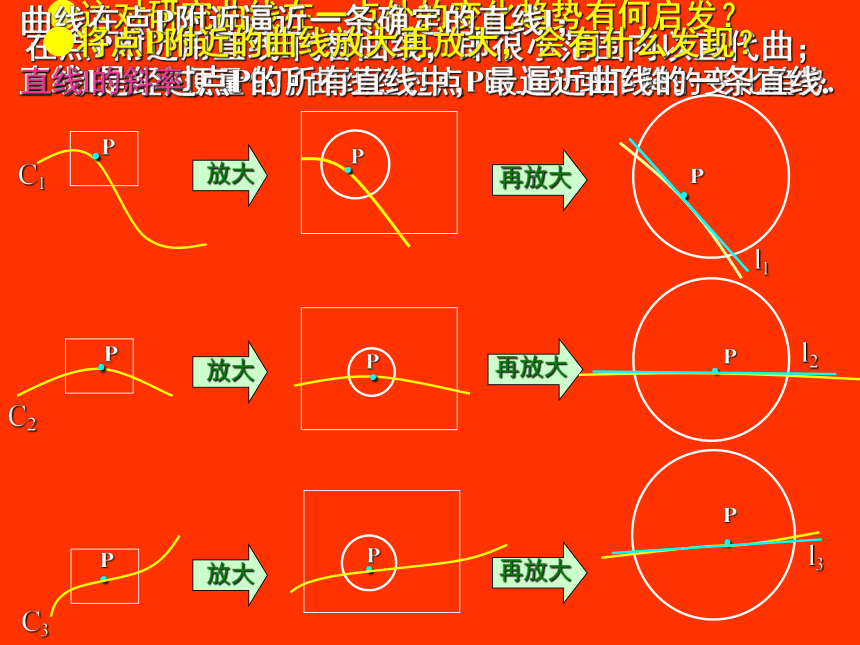
●这对研究曲线在一点处的变化趋势有何启发?
在点P附近用直线l代替曲线,即很小范围内以直代曲;
再放大
再放大
·
P
再放大
P
·
P
·
放大
放大
放大
·
P
·
P
·
P
·
P
P
·
·
P
C1
C2
C3
l1
l3
l2
曲线在点P附近逼近一条确定的直线l;
直线l是经过点P的所有直线中,最逼近曲线的一条直线.
●将点P附近的曲线放大再放大,会有什么发现?
直线l的斜率
P
Q
o
x
y
y=f(x)
割线
切线
T
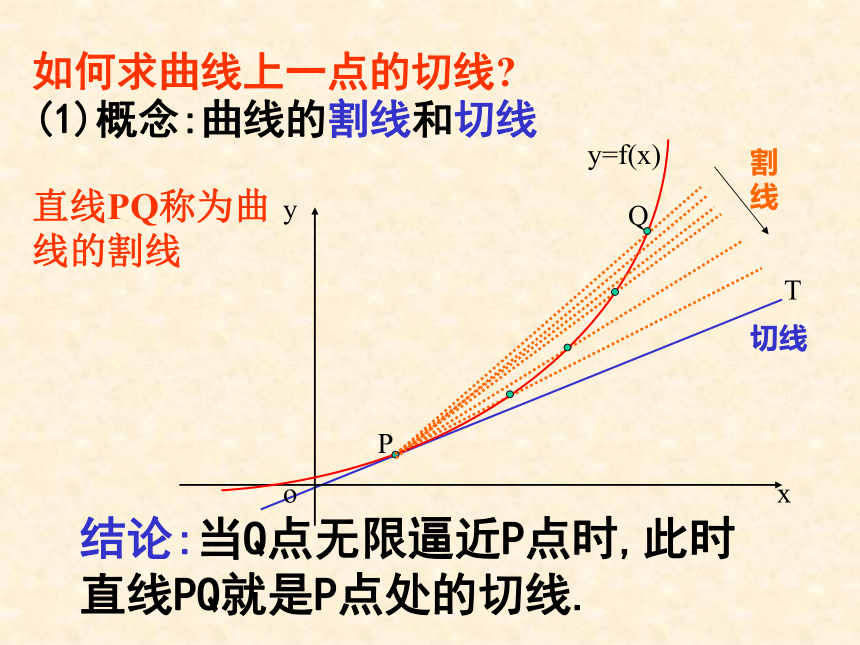
(1)概念:曲线的割线和切线
结论:当Q点无限逼近P点时,此时
直线PQ就是P点处的切线.
直线PQ称为曲线的割线
如何求曲线上一点的切线
(2)如何求割线的斜率
o
x
y
y=f(x)
P
x
Q
x+△x
P
Q
o
x
y
y=f(x)
割线
切线
T
(3)如何求切线的斜率
割线逼近切线的思想
例1:试求f (x)=x2+1在x=1处的切线斜率.
当△x无限趋近于0时,
割 线 逼 近 切 线,
割线斜率逼近切线斜率
找到定点P的坐标设出动点Q的坐标
求出割线斜率
2.求出割线PQ的斜率
,并化简.
求曲线y=f(x)上一点P(x0,f(x0))处
切线斜率的一般步骤:
3. 令Δx 趋向于0,若上式中的割线斜率“逼近”
一个常数,则其即为所求切线斜率
1.设曲线上另一点Q(x0 +Δx,f(x0 + Δx))
例2:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
因此,切线方程为y-2=2(x-1),即y=2x.
求曲线上某点P处的切线方程的基本步骤:
1.求出割线PQ的斜率
3.利用点斜式求出切线的方程
例3.已知f(x)= , 求曲线y=f(x)在x=1处的切线的斜率.
例4.求过点(1 , 0)与曲线y=-x2相切的直线的斜率.
小 结
1、曲线上一点P处的切线是过点P的所有直线中最接近P点附近曲线的直线,则P点处的变化趋势可以由该点处的切线反映。(局部以直代曲)
● 2、根据定义,利用割线逼近切线的方法, 可以求出曲线在一点处的切线斜率和方程。
割线PQ
P点处的切线
Q无限逼近P时
割线PQ的斜率
P点处的切线斜率
Q无限逼近P时
令横坐标无限接近
课堂练习
曲线上一点处的切线
平均变化率
一般的,函数 在区间上 的平均变化率为
复均变化率近似地刻画了曲线在某一区间上的变化趋势.
·
P
问题:如何精确地刻画曲线在某一点处的变化趋势呢
直线l的斜率便量化了曲线经过点P时上升或下降的变化趋势.
●这对研究曲线在一点处的变化趋势有何启发?
在点P附近用直线l代替曲线,即很小范围内以直代曲;
再放大
再放大
·
P
再放大
P
·
P
·
放大
放大
放大
·
P
·
P
·
P
·
P
P
·
·
P
C1
C2
C3
l1
l3
l2
曲线在点P附近逼近一条确定的直线l;
直线l是经过点P的所有直线中,最逼近曲线的一条直线.
●将点P附近的曲线放大再放大,会有什么发现?
直线l的斜率
P
Q
o
x
y
y=f(x)
割线
切线
T
(1)概念:曲线的割线和切线
结论:当Q点无限逼近P点时,此时
直线PQ就是P点处的切线.
直线PQ称为曲线的割线
如何求曲线上一点的切线
(2)如何求割线的斜率
o
x
y
y=f(x)
P
x
Q
x+△x
P
Q
o
x
y
y=f(x)
割线
切线
T
(3)如何求切线的斜率
割线逼近切线的思想
例1:试求f (x)=x2+1在x=1处的切线斜率.
当△x无限趋近于0时,
割 线 逼 近 切 线,
割线斜率逼近切线斜率
找到定点P的坐标设出动点Q的坐标
求出割线斜率
2.求出割线PQ的斜率
,并化简.
求曲线y=f(x)上一点P(x0,f(x0))处
切线斜率的一般步骤:
3. 令Δx 趋向于0,若上式中的割线斜率“逼近”
一个常数,则其即为所求切线斜率
1.设曲线上另一点Q(x0 +Δx,f(x0 + Δx))
例2:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
因此,切线方程为y-2=2(x-1),即y=2x.
求曲线上某点P处的切线方程的基本步骤:
1.求出割线PQ的斜率
3.利用点斜式求出切线的方程
例3.已知f(x)= , 求曲线y=f(x)在x=1处的切线的斜率.
例4.求过点(1 , 0)与曲线y=-x2相切的直线的斜率.
小 结
1、曲线上一点P处的切线是过点P的所有直线中最接近P点附近曲线的直线,则P点处的变化趋势可以由该点处的切线反映。(局部以直代曲)
● 2、根据定义,利用割线逼近切线的方法, 可以求出曲线在一点处的切线斜率和方程。
割线PQ
P点处的切线
Q无限逼近P时
割线PQ的斜率
P点处的切线斜率
Q无限逼近P时
令横坐标无限接近
课堂练习
