1.1.2(2).瞬时速度,瞬时加速度(2010-12-22 19.38.42)
文档属性
| 名称 | 1.1.2(2).瞬时速度,瞬时加速度(2010-12-22 19.38.42) |

|
|
| 格式 | rar | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-28 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
3.1.2(2)
瞬时速度 瞬时加速度
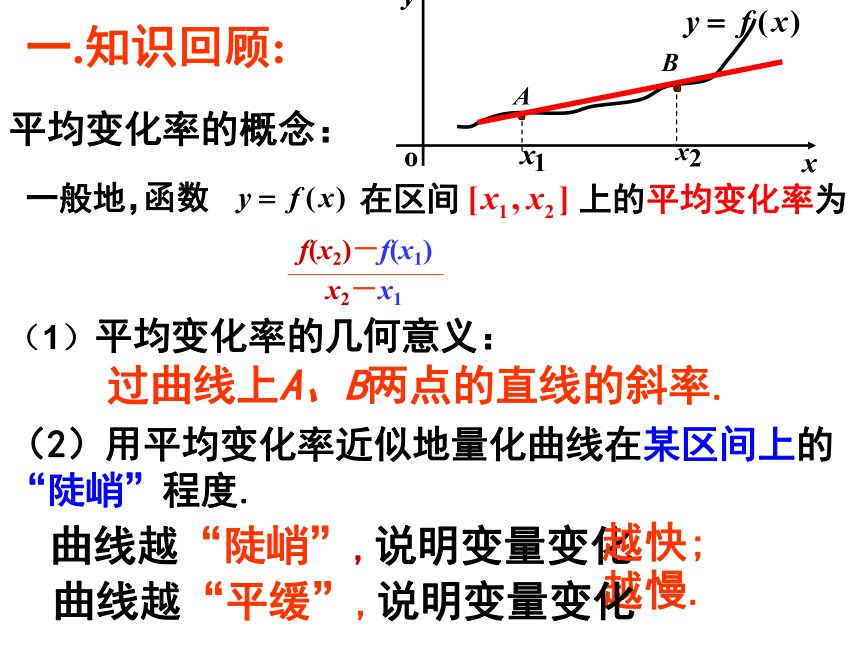
平均变化率的概念:
(2)用平均变化率近似地量化曲线在某区间上的 “陡峭”程度.
曲线越“陡峭”,说明变量变化
越快;
越慢.
曲线越“平缓”,说明变量变化
(1)平均变化率的几何意义:
过曲线上A、B两点的直线的斜率.
f(x2)-f(x1)
x2-x1
x
y
o
函数
在区间 上的平均变化率为
一般地,
一.知识回顾:
求切线的斜率的步骤
(1)设点P
Q
(2)求割线的斜率
(3)当 无限趋近于0时,
无限趋近于一个常数,
此常数即为点P处切线的斜率
练习
拓展研究
平均变化率的作用
近似地刻画了曲线在某一区间上的变化趋势.
二.问题情景:
1.物理意义——瞬时速度
在物理学中,我们学过平均速度
三.新课讲解:
平均速度反映了在某一段时间内
运动的快慢程度,那么,如何刻画在
某一时刻运动的快慢程度呢
实例:
某人去蹦极,假设他下降的运动
符合方程 ,请同学们计算他
从3秒到5秒间的平均速度,如何计算出
在第3秒时的速度,即t=3时的瞬时速度呢
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(1) 物体在时间区间[3,5]上的平均速度;
(2) 物体在t=3(s)时的瞬时速度.
s
D
s
s(3+
D
t
)
O
s(3)
分析:
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(1) 物体在时间区间[3,5]上的平均速度;
(2) 物体在t=3(s)时的瞬时速度.
(3) 物体在t=t0(s)时的瞬时速度.
分析:
设物体作直线运动所经过的路程为s=s(t). 以t0为起始时刻,物体在 t时间内的平均速度为
这个常数就是物体在t0时刻的瞬时速度.
当 t 0时,
结论:
t
t
t
t
s
s
D
-
D
+
=
)
(
)
(
0
0
小结:
求物体运动的瞬时速度:
(1)求位移增量: Δs=s(t+Δt)-s(t)
(2)求平均速度:
(3)求瞬时速度
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(4) 物体在t=3(s)时的瞬时加速度.
设物体作直线运动,t(s)时的速度为v=v(t). 以t0为起始时刻,物体在 t时间内的平均加速度为
这个常数就是物体在t0时刻的
瞬时加速度.
当 t 0时,
t
t
v
t
t
v
t
v
D
-
D
+
=
D
D
=
)
(
)
(
0
0
2、瞬时加速度
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(4) 物体在t=3(s)时的瞬时加速度.
变:物体在t=t0(s)时的瞬时加速度.
2.物理意义——瞬时加速度
设一辆轿车在公路上做加速直线运动,假设t秒时的速度为 ,求t=5秒时轿车的加速度.
t=t0(s)时的轿车的加速度?
例4.已知一物体的运动方程是s= , 求此物体在t=1和t=4时的瞬时速度.
巩固:
小结:
(1)在求瞬时速度时,先利用平均变化率求
出平均速度,再令 ,求出瞬时速度
(2)在求瞬时加速度时,先利用平均变化率求出平均加速度,再令 ,求出瞬时加速度.
平均变化率 瞬时变化率
重要结论:
3.1.2(2)
瞬时速度 瞬时加速度
平均变化率的概念:
(2)用平均变化率近似地量化曲线在某区间上的 “陡峭”程度.
曲线越“陡峭”,说明变量变化
越快;
越慢.
曲线越“平缓”,说明变量变化
(1)平均变化率的几何意义:
过曲线上A、B两点的直线的斜率.
f(x2)-f(x1)
x2-x1
x
y
o
函数
在区间 上的平均变化率为
一般地,
一.知识回顾:
求切线的斜率的步骤
(1)设点P
Q
(2)求割线的斜率
(3)当 无限趋近于0时,
无限趋近于一个常数,
此常数即为点P处切线的斜率
练习
拓展研究
平均变化率的作用
近似地刻画了曲线在某一区间上的变化趋势.
二.问题情景:
1.物理意义——瞬时速度
在物理学中,我们学过平均速度
三.新课讲解:
平均速度反映了在某一段时间内
运动的快慢程度,那么,如何刻画在
某一时刻运动的快慢程度呢
实例:
某人去蹦极,假设他下降的运动
符合方程 ,请同学们计算他
从3秒到5秒间的平均速度,如何计算出
在第3秒时的速度,即t=3时的瞬时速度呢
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(1) 物体在时间区间[3,5]上的平均速度;
(2) 物体在t=3(s)时的瞬时速度.
s
D
s
s(3+
D
t
)
O
s(3)
分析:
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(1) 物体在时间区间[3,5]上的平均速度;
(2) 物体在t=3(s)时的瞬时速度.
(3) 物体在t=t0(s)时的瞬时速度.
分析:
设物体作直线运动所经过的路程为s=s(t). 以t0为起始时刻,物体在 t时间内的平均速度为
这个常数就是物体在t0时刻的瞬时速度.
当 t 0时,
结论:
t
t
t
t
s
s
D
-
D
+
=
)
(
)
(
0
0
小结:
求物体运动的瞬时速度:
(1)求位移增量: Δs=s(t+Δt)-s(t)
(2)求平均速度:
(3)求瞬时速度
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(4) 物体在t=3(s)时的瞬时加速度.
设物体作直线运动,t(s)时的速度为v=v(t). 以t0为起始时刻,物体在 t时间内的平均加速度为
这个常数就是物体在t0时刻的
瞬时加速度.
当 t 0时,
t
t
v
t
t
v
t
v
D
-
D
+
=
D
D
=
)
(
)
(
0
0
2、瞬时加速度
应用:
例1.物体作自由落体运动,位移s(m)与时间
t(s)的关系为方程: (g=10m/s2)求:
(4) 物体在t=3(s)时的瞬时加速度.
变:物体在t=t0(s)时的瞬时加速度.
2.物理意义——瞬时加速度
设一辆轿车在公路上做加速直线运动,假设t秒时的速度为 ,求t=5秒时轿车的加速度.
t=t0(s)时的轿车的加速度?
例4.已知一物体的运动方程是s= , 求此物体在t=1和t=4时的瞬时速度.
巩固:
小结:
(1)在求瞬时速度时,先利用平均变化率求
出平均速度,再令 ,求出瞬时速度
(2)在求瞬时加速度时,先利用平均变化率求出平均加速度,再令 ,求出瞬时加速度.
平均变化率 瞬时变化率
重要结论:
