1.2.1常见函数的导数
图片预览





文档简介
(共13张PPT)
常见函数的导数
1.导数的概念
函数y=f(x)在区间(a,b)上有定义,x0∈(a,b),当△x无限趋近于0时,比值
无限趋近于一个常数A,则称f(x)在x=x0处可导,并称常数A为函数在点x=x0处的导数,记作
复习回顾
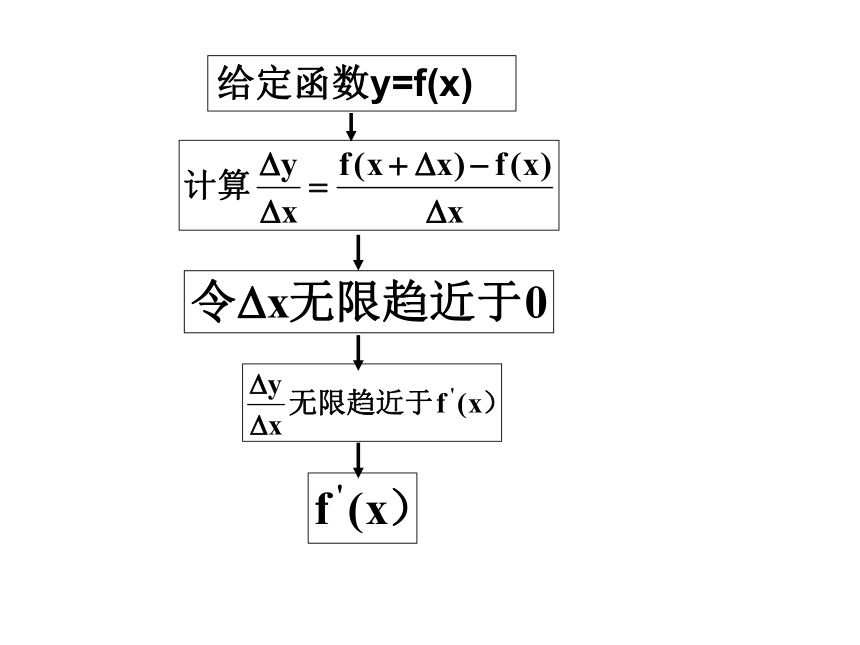
步骤:
说明:上面的方法中把x换x0即为求函数在点x0处的导数.
3.求函数的导数的方法是:
2.函数y=f(x)在点x0处的导数的几何意义:
曲线y=f(x)在点P(x0 ,f(x0))处的切线的斜率.
复习回顾
给定函数y=f(x)
探究一:
导数值为常数3
探究结果:
探究二:
探究结果:
导数值不为常数但有规律
探究三:
(2)f(x)=x2
(3)f(x)=x3
求下列各函数的导数:
基本初等函数求导公式:
例1.求下列函数的导数
发现:对于幂函数应该将所给函数化为分数指数幂后,再用求导的公式.
例2. 求下列函数的导数
(1)f(x)=2x (2) (3)
例3.(1)分别求出: ①f(x)=lg4 ②f(x)=lgx ③f(x)=log3x 的导数.
(2)已知
求
例4.(1)已知P(-1 , 1), Q(2 , 4)是曲线y=x2上的两点, 则与直线PQ平行的曲线y=x2的切线方程是_________ .
(2)求双曲线y= 与抛物线y= 在交点处的切线方程.
基本初等函数求导公式:
常见函数的导数
1.导数的概念
函数y=f(x)在区间(a,b)上有定义,x0∈(a,b),当△x无限趋近于0时,比值
无限趋近于一个常数A,则称f(x)在x=x0处可导,并称常数A为函数在点x=x0处的导数,记作
复习回顾
步骤:
说明:上面的方法中把x换x0即为求函数在点x0处的导数.
3.求函数的导数的方法是:
2.函数y=f(x)在点x0处的导数的几何意义:
曲线y=f(x)在点P(x0 ,f(x0))处的切线的斜率.
复习回顾
给定函数y=f(x)
探究一:
导数值为常数3
探究结果:
探究二:
探究结果:
导数值不为常数但有规律
探究三:
(2)f(x)=x2
(3)f(x)=x3
求下列各函数的导数:
基本初等函数求导公式:
例1.求下列函数的导数
发现:对于幂函数应该将所给函数化为分数指数幂后,再用求导的公式.
例2. 求下列函数的导数
(1)f(x)=2x (2) (3)
例3.(1)分别求出: ①f(x)=lg4 ②f(x)=lgx ③f(x)=log3x 的导数.
(2)已知
求
例4.(1)已知P(-1 , 1), Q(2 , 4)是曲线y=x2上的两点, 则与直线PQ平行的曲线y=x2的切线方程是_________ .
(2)求双曲线y= 与抛物线y= 在交点处的切线方程.
基本初等函数求导公式:
