1.3.3函数的最大(小)值与导数(81)
文档属性
| 名称 | 1.3.3函数的最大(小)值与导数(81) |

|
|
| 格式 | rar | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-28 15:26:14 | ||
图片预览




文档简介
(共16张PPT)
函数的最大值与最小值
导数的应用二、求函数的极值
注:导数等于零的点不一定是极值点.
函数的极值不是唯一的,即一个函数在某区间上或定义域内极大值或极小值可以不止一个。
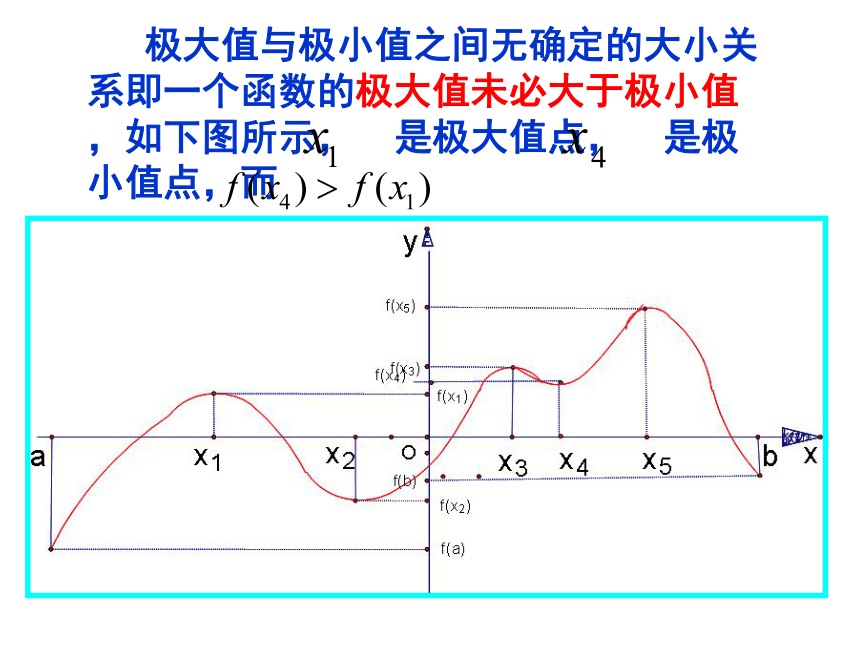
极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值,如下图所示, 是极大值点, 是极小值点,而
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,求出极大值和极小值.
求函数f(x)的极值的步骤:
(1)求导数f′(x);
(2)求方程f′(x)=0的根
口诀:左负右正为极小,左正右负为极大。
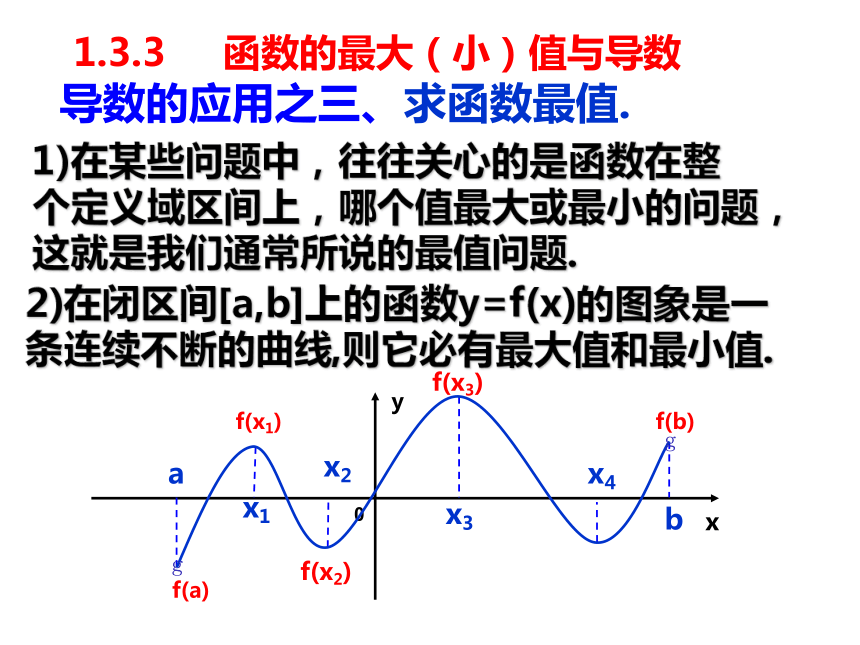
导数的应用之三、求函数最值.
1)在某些问题中,往往关心的是函数在整
个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题.
2)在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
1.3.3 函数的最大(小)值与导数
x
y
0
a
b
x1
x2
x3
x4
f(a)
f(x3)
f(b)
f(x1)
f(x2)
最值的概念(最大值与最小值)
如果在函数定义域I内存在x0,使得对任意的x∈I,
若总有f(x) ≤f(x0),则称f(x0)为函数f(x)在定义域上的最大值;
若总有f(x) ≥f(x0),则称f(x0)为函数f(x)在定义域上的最小值。
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
y=f(x)
y=f(x)
y=f(x)
y=f(x)
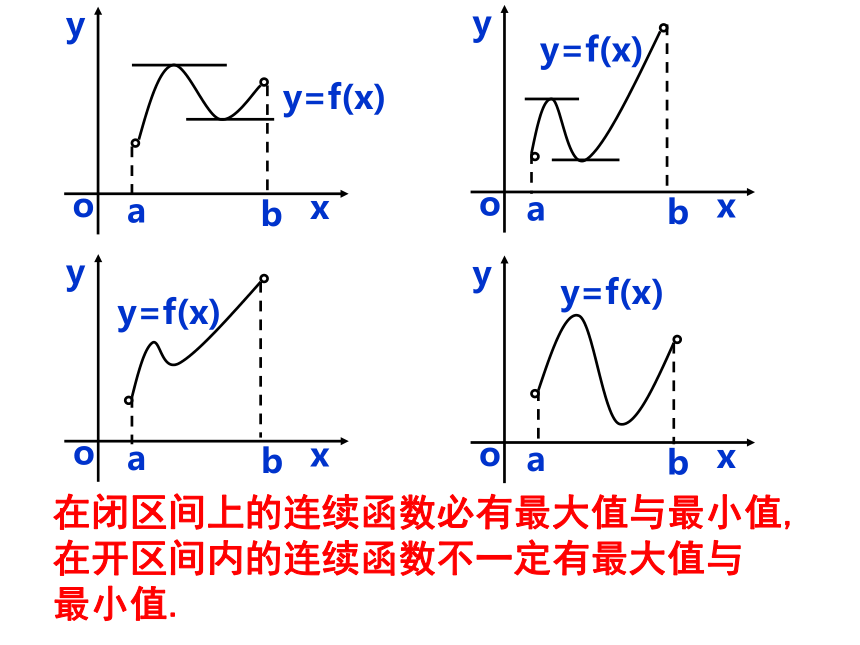
在闭区间上的连续函数必有最大值与最小值,
在开区间内的连续函数不一定有最大值与
最小值.
导数的应用之三、求函数最值.
(2)将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个最小值.
求f(x)在闭区间[a,b]上的最值的步骤
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
二.如何求函数的最值
(1)利用函数的单调性;
(2)利用函数的图象;
(3)利用函数的导数;
如:求y=2x+1在区间[1,3]上的最值.
如:求y=(x-2)2+3在区间[1,3]上的最值.
例1、求函数f(x)=x4 -2x2+5在区间
[-2,2] 上的最大值和最小值
数学应用
例2.求f(x)=x/2+sinx在区间[0,2 ]上的最大值与最小值.
数学应用
例3:(江西卷)
已知函数f(x)=x3+ax2+bx+c在x= 与x=1时都取得极值
1)求a、b的值与函数f(x)的单调区间;
2)若对x∈[-1,2],不等式f(x)数学应用
例4.已知函数f(x)=-x2+8x,g(x)=6lnx+m,是否存在实数m使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
(作业第11题(2))
数学应用
例4:已知函数f(x)=-x3+3x2+9x+a
1)求f(x)的单调递减区间;
2)若f(x)在区间[-2,2]上的最大值
为20,求它在该区间上的最小值.
数学应用
一.是利用函数性质
二.是利用不等式
三.是利用导数
求函数最值的一般方法:
注:若函数f(x)在[a,b]上连续,在(a,b)内可导,则导数法求f(x)在[a,b]上的最值的步骤如下:
①求y=f(x)在(a,b)内的极值;
②将函数y=f(x)的各极值与f(a)、f(b)作比较,其中最大的一个为最大值,最小的一个为最小值.
函数的最大值与最小值
导数的应用二、求函数的极值
注:导数等于零的点不一定是极值点.
函数的极值不是唯一的,即一个函数在某区间上或定义域内极大值或极小值可以不止一个。
极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值,如下图所示, 是极大值点, 是极小值点,而
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,求出极大值和极小值.
求函数f(x)的极值的步骤:
(1)求导数f′(x);
(2)求方程f′(x)=0的根
口诀:左负右正为极小,左正右负为极大。
导数的应用之三、求函数最值.
1)在某些问题中,往往关心的是函数在整
个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题.
2)在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
1.3.3 函数的最大(小)值与导数
x
y
0
a
b
x1
x2
x3
x4
f(a)
f(x3)
f(b)
f(x1)
f(x2)
最值的概念(最大值与最小值)
如果在函数定义域I内存在x0,使得对任意的x∈I,
若总有f(x) ≤f(x0),则称f(x0)为函数f(x)在定义域上的最大值;
若总有f(x) ≥f(x0),则称f(x0)为函数f(x)在定义域上的最小值。
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
y=f(x)
y=f(x)
y=f(x)
y=f(x)
在闭区间上的连续函数必有最大值与最小值,
在开区间内的连续函数不一定有最大值与
最小值.
导数的应用之三、求函数最值.
(2)将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个最小值.
求f(x)在闭区间[a,b]上的最值的步骤
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
二.如何求函数的最值
(1)利用函数的单调性;
(2)利用函数的图象;
(3)利用函数的导数;
如:求y=2x+1在区间[1,3]上的最值.
如:求y=(x-2)2+3在区间[1,3]上的最值.
例1、求函数f(x)=x4 -2x2+5在区间
[-2,2] 上的最大值和最小值
数学应用
例2.求f(x)=x/2+sinx在区间[0,2 ]上的最大值与最小值.
数学应用
例3:(江西卷)
已知函数f(x)=x3+ax2+bx+c在x= 与x=1时都取得极值
1)求a、b的值与函数f(x)的单调区间;
2)若对x∈[-1,2],不等式f(x)
例4.已知函数f(x)=-x2+8x,g(x)=6lnx+m,是否存在实数m使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
(作业第11题(2))
数学应用
例4:已知函数f(x)=-x3+3x2+9x+a
1)求f(x)的单调递减区间;
2)若f(x)在区间[-2,2]上的最大值
为20,求它在该区间上的最小值.
数学应用
一.是利用函数性质
二.是利用不等式
三.是利用导数
求函数最值的一般方法:
注:若函数f(x)在[a,b]上连续,在(a,b)内可导,则导数法求f(x)在[a,b]上的最值的步骤如下:
①求y=f(x)在(a,b)内的极值;
②将函数y=f(x)的各极值与f(a)、f(b)作比较,其中最大的一个为最大值,最小的一个为最小值.
