1.3.2函数的极值(1)
图片预览







文档简介
(共20张PPT)
一般地,设函数y=f(x)在某个区间内可导,
若f(x)在该区间f′(x)>0,
则f(x)为该区间上增函数;
则f(x)为该区间上减函数.
若f(x)在该区间f′(x)<0,
复习回顾
1、导数符号与函数单调性之间的关系
2、 一般地,设函数y=f(x)在区间(a,b)内可导,
f′(x)≥0对x∈(a,b)恒成立.
若f(x)在(a,b)上单调递增
f′(x)≤ 0对x∈(a,b)恒成立.
若f(x)在(a,b)上单调递减
3、利用导数求函数单调区间的步骤:
1.已知函数 ,求函数的单调区间.
2. 若函数f(x)=ax3+3x2-x+1 在R上是单调减函数,则实数a的取值范围为_______.
变题1: 若函数f(x)=ax3+bx2-x+1 的递减区间为(-2,3),则实数a=_____,b=______.
变题2:若函数f(x)=x3+3ax2-x+1 在[1,3]上是减函数,则实数a的取值范围为_______.
快速练习
1、本班个子最高的人;
2、函数y=x2在[-1,1]上,当x=0时取最大值.
都是在一个局部范围内的最值问题
极值
问题情境
79.函数的极值(1)
x
O
y
x1
x2
x3
x4
x5
x6
.P
. Q
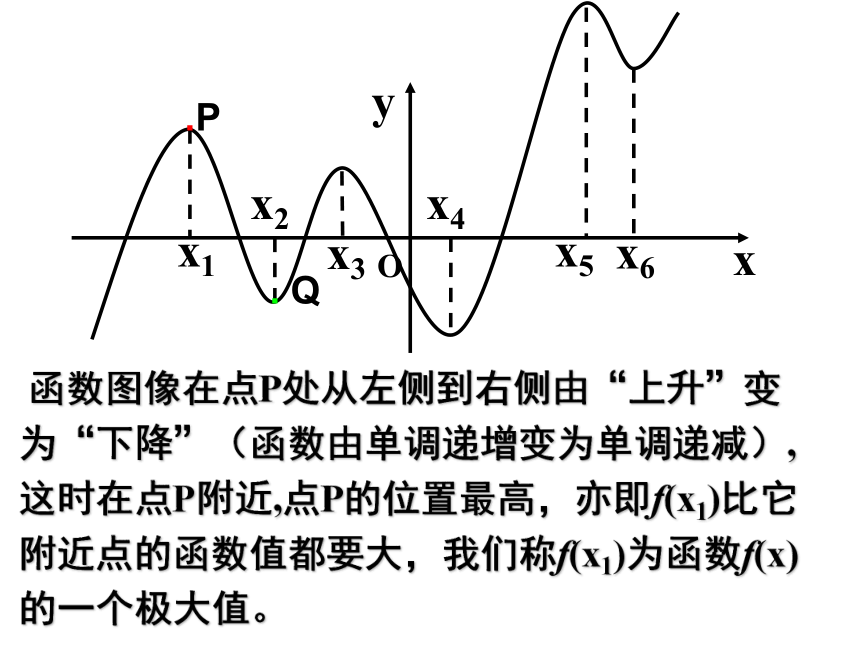
函数图像在点P处从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),这时在点P附近,点P的位置最高,亦即f(x1)比它附近点的函数值都要大,我们称f(x1)为函数f(x)的一个极大值。
设函数y=f(x)在x=x0及其附近有定义,
(1)如果在x=x0处的函数值比它附近所有各点的函数值都大,即f(x)(2)如果在x=x0处的函数值比它附近所有各点的函数值都小,即f(x)>f(x0),则称 f(x0)是函数y=f(x)的一个极小值.记作:y极小值=f(x0)
极大值与极小值统称为极值, x0叫做函数的极值点.
1.函数极值的定义
数学建构
x
O
y
x1
x2
x3
x4
x5
x6
O
O
O
x
y
x
y
O
找出下图中的极值点
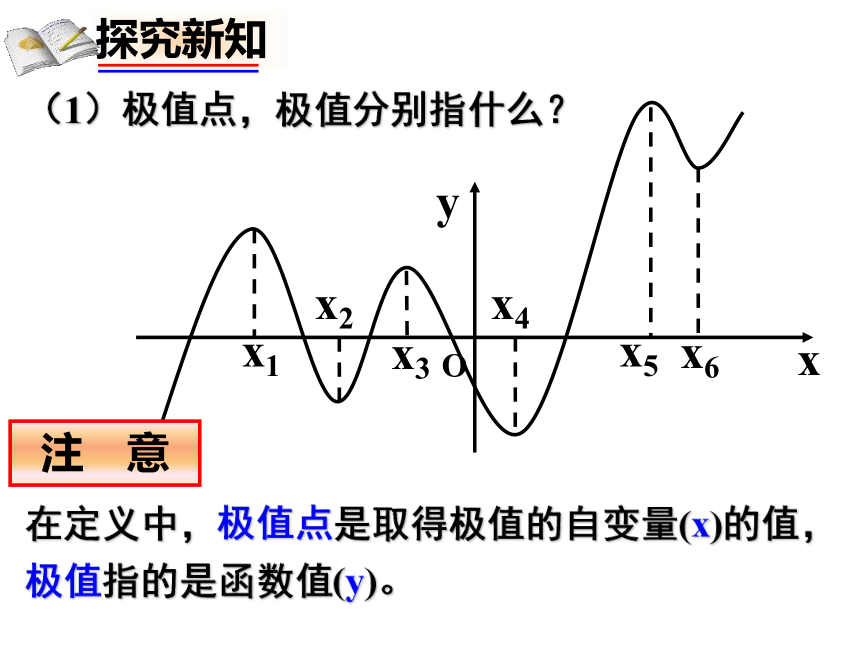
(1)极值点,极值分别指什么?
x
O
y
x1
x2
x3
x4
x5
x6
注 意
在定义中,极值点是取得极值的自变量(x)的值,极值指的是函数值(y)。
探究新知
(2)极值是一个局部概念还是在函数的整个的定义域内?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
注 意:
探究新知
(3)函数的极值不唯一
(4)极大值与极小值之间有无确定的大小关系?
x
O
y
x1
x2
x3
x4
x5
x6
.P
. Q
数学建构
2、极值点与导数的关系
(1)如果f′(x0)=0, 并且在x0附近的左侧f′(x)>0 ,右侧f′(x)<0,那么f(x0)是极大值.
x0左侧 x0
x0右侧
增 极点值 减
(2)如果f′(x0)=0, 并且在x0附近的左侧f′(x)<0 ,右侧f′(x)>0,那么f(x0)是极小值.
x0左侧 x0
x0右侧
减 极点值 增
2、极值点与导数的关系
数学建构
数学应用
例1:求f(x)=x2-x-2的极值
(4)列表:用导数值为0的点顺次将函数的定义区间分成若干开区间,并列成表格.检查f′(x)在方程根左右的值的符号.
求函数f(x)极值的步骤:
(2)求导数f′(x);
(3)求方程f′(x)=0的根
(x为极值点)
(5)求出极值.
左正右负—极大值
左负右正—极小值
(1)求函数的定义域
解:
当x变化时,f′(x) ,f(x)的变化情况如下表
例2:求 的极值
令f′(x)=0,解得x1=-2,x2=2
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗
∴当x=-2时,y有极大值且y极大值=
当x=2时,y有极小值且y极小值=
数学应用
例3:求y=(x2-1)3+1的极值。
练习:求函数的极值(见教案练习2)
数学应用
O
O
y
y
(6)可导函数的极值点的导数必为零,那么导数为零的一定是极值点吗?
导数为零的不一定是极值点。
y=x2
y=x3
探究新知
注 意
(7)不可导点是否可为极值点?
O
O
x
y
y=|x|
O
O
x
注 意
是 为极值点的既不充分也不必要条件
也即用 求极值即可能增解也可能漏解,本质是用单调性来求极值。
变题1:若函数y=x3+x2+mx+1有三个单调区间,则实数m的取值范围是 .
变题2:若函数y=x3+x2+mx+1在(0,1)上单调递减,在(1,+∞)上单调递增,则实数m的值是 .
变题3:若函数y=x3+x2+mx+1在 上既不是单调递增函数也不是单调递减函数,则整数m的值是____________ .
变题4:若函数y=x3+x2+mx+1的单调递减区间是 ,则实数m的值是______.
2.若函数y=x3+x2+mx+1是 R上的单调函数,则实数m的取值范围是__________.
1.已知函数 ,求函数的单调区间.
3. 若函数f(x)=x3-ax2+1 在(0,2)内单调递减,则实数a的取值范围为_______.
练习
练习:求函数的极值
一般地,设函数y=f(x)在某个区间内可导,
若f(x)在该区间f′(x)>0,
则f(x)为该区间上增函数;
则f(x)为该区间上减函数.
若f(x)在该区间f′(x)<0,
复习回顾
1、导数符号与函数单调性之间的关系
2、 一般地,设函数y=f(x)在区间(a,b)内可导,
f′(x)≥0对x∈(a,b)恒成立.
若f(x)在(a,b)上单调递增
f′(x)≤ 0对x∈(a,b)恒成立.
若f(x)在(a,b)上单调递减
3、利用导数求函数单调区间的步骤:
1.已知函数 ,求函数的单调区间.
2. 若函数f(x)=ax3+3x2-x+1 在R上是单调减函数,则实数a的取值范围为_______.
变题1: 若函数f(x)=ax3+bx2-x+1 的递减区间为(-2,3),则实数a=_____,b=______.
变题2:若函数f(x)=x3+3ax2-x+1 在[1,3]上是减函数,则实数a的取值范围为_______.
快速练习
1、本班个子最高的人;
2、函数y=x2在[-1,1]上,当x=0时取最大值.
都是在一个局部范围内的最值问题
极值
问题情境
79.函数的极值(1)
x
O
y
x1
x2
x3
x4
x5
x6
.P
. Q
函数图像在点P处从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),这时在点P附近,点P的位置最高,亦即f(x1)比它附近点的函数值都要大,我们称f(x1)为函数f(x)的一个极大值。
设函数y=f(x)在x=x0及其附近有定义,
(1)如果在x=x0处的函数值比它附近所有各点的函数值都大,即f(x)
极大值与极小值统称为极值, x0叫做函数的极值点.
1.函数极值的定义
数学建构
x
O
y
x1
x2
x3
x4
x5
x6
O
O
O
x
y
x
y
O
找出下图中的极值点
(1)极值点,极值分别指什么?
x
O
y
x1
x2
x3
x4
x5
x6
注 意
在定义中,极值点是取得极值的自变量(x)的值,极值指的是函数值(y)。
探究新知
(2)极值是一个局部概念还是在函数的整个的定义域内?
极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小。
注 意:
探究新知
(3)函数的极值不唯一
(4)极大值与极小值之间有无确定的大小关系?
x
O
y
x1
x2
x3
x4
x5
x6
.P
. Q
数学建构
2、极值点与导数的关系
(1)如果f′(x0)=0, 并且在x0附近的左侧f′(x)>0 ,右侧f′(x)<0,那么f(x0)是极大值.
x0左侧 x0
x0右侧
增 极点值 减
(2)如果f′(x0)=0, 并且在x0附近的左侧f′(x)<0 ,右侧f′(x)>0,那么f(x0)是极小值.
x0左侧 x0
x0右侧
减 极点值 增
2、极值点与导数的关系
数学建构
数学应用
例1:求f(x)=x2-x-2的极值
(4)列表:用导数值为0的点顺次将函数的定义区间分成若干开区间,并列成表格.检查f′(x)在方程根左右的值的符号.
求函数f(x)极值的步骤:
(2)求导数f′(x);
(3)求方程f′(x)=0的根
(x为极值点)
(5)求出极值.
左正右负—极大值
左负右正—极小值
(1)求函数的定义域
解:
当x变化时,f′(x) ,f(x)的变化情况如下表
例2:求 的极值
令f′(x)=0,解得x1=-2,x2=2
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗
∴当x=-2时,y有极大值且y极大值=
当x=2时,y有极小值且y极小值=
数学应用
例3:求y=(x2-1)3+1的极值。
练习:求函数的极值(见教案练习2)
数学应用
O
O
y
y
(6)可导函数的极值点的导数必为零,那么导数为零的一定是极值点吗?
导数为零的不一定是极值点。
y=x2
y=x3
探究新知
注 意
(7)不可导点是否可为极值点?
O
O
x
y
y=|x|
O
O
x
注 意
是 为极值点的既不充分也不必要条件
也即用 求极值即可能增解也可能漏解,本质是用单调性来求极值。
变题1:若函数y=x3+x2+mx+1有三个单调区间,则实数m的取值范围是 .
变题2:若函数y=x3+x2+mx+1在(0,1)上单调递减,在(1,+∞)上单调递增,则实数m的值是 .
变题3:若函数y=x3+x2+mx+1在 上既不是单调递增函数也不是单调递减函数,则整数m的值是____________ .
变题4:若函数y=x3+x2+mx+1的单调递减区间是 ,则实数m的值是______.
2.若函数y=x3+x2+mx+1是 R上的单调函数,则实数m的取值范围是__________.
1.已知函数 ,求函数的单调区间.
3. 若函数f(x)=x3-ax2+1 在(0,2)内单调递减,则实数a的取值范围为_______.
练习
练习:求函数的极值
