1.3.2函数的极值(2)

(共19张PPT)
80.函数的极值（2）
x
O
y
x1
x2
x3
x4
x5
x6
.P
. Q
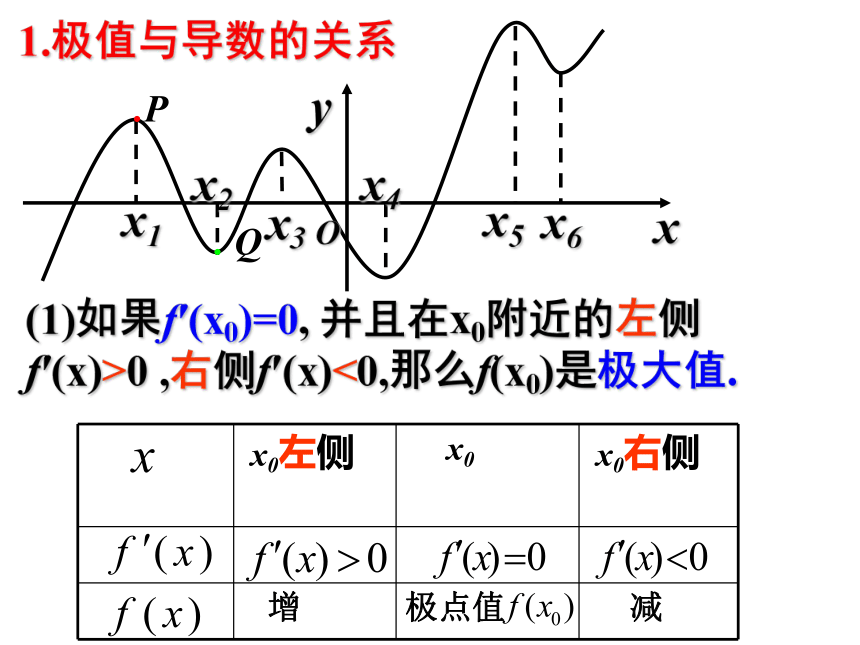
1.极值与导数的关系
(1)如果f′(x0)=0, 并且在x0附近的左侧f′(x)>0 ,右侧f′(x)<0,那么f(x0)是极大值.
x0左侧 x0
x0右侧
增 极点值 减
(2)如果f′(x0)=0, 并且在x0附近的左侧f′(x)<0 ,右侧f′(x)>0,那么f(x0)是极小值.
x0左侧 x0 x0右侧
减 极点值f(x0) 增
1.极值与导数的关系
(4)列表：用函数的导数为0的点顺次将函数的定义区间分成若干开区间，并列成表格.检查f′(x)在方程根左右的值的符号.
2.求函数f(x)极值的步骤:
(2)求导数f′(x);
(3)求方程f′(x)=0的根
(5)求出极值.
左正右负—极大值
左负右正—极小值
(1)求函数的定义域
9(2).
解:
令
解得：x1=0,x2=2
列表如下：
x
f(x)
(-∞,0)
0
(0,2)
2
(2,+∞)
-
0
+
0
-
↑
极小值f(0)
极大值f(2)
所以，函数f(x)的极小值为f(0)=0
函数f(x)的极大值为f(2)=
例.确定函数 的单调区间，并求函
数的极大、极小值
解:
列表如下：
x
f(x)
(-∞,-1)
-1
(-1,1)
1
(1,+∞)
-
0
+
0
-
↑
极小值f(-1)
极大值f(1)
2.已知函数y=－x3、y=cos2x、y=tanx－x、y=1/x，其中x=0是极值点的函数是 _____.
1.对可导函数，在一点两侧的导数异号是这点为极值点的___________条件.
y=cos2x
充要
学生活动
3.下列四种说法正确的个数为_________.
①函数在闭区间上的极大值一定比极小值大②函数在闭区间上的最大值一定是极大值 ③对于f(x)=x3+px2+2x+1，若|p|＜ ，则f(x)无极值 ④函数f(x)在区间(a，b)上一定存在最值
1
学生活动
4.函数f(x)的定义域为开区间(a,b),导函数 f '(x)在(a,b)内的图象如图所示，则函数f (x)在开区间(a,b)内极小值点的个数为_____.
x1
x2
x3
1
学生活动
数学应用
例1.已知函数f(x)=x3-ax2-bx+a2在x=1处有极值为10,求a、b的值.
小结:若函数y=f(x)可导,x0是极值点y0是
极值,则
注意检验!
解: =3x2-2ax-b=0有一个根x=1,故3-2a-b=0.①
又f(1)=10,故1-a-b+a2=10.②
由①、②解得 或
当a=3,b=-3时, ,此时f(x)在x=1处无极值,不合题意.
当a=-4,b=11时,
-3/111时, ,此时x=1是极值点.
从而所求的解为a=-4,b=11.
7、三次函数当x=1时有极大值4，当x=3时有极小值0，且函数过原点，则此函数的表达式是_____________.
8、已知函数 ,则f(1)与f(-1)的大小关系是_____________.
79作业讲评
1. 函数f(x)=asinx+ sin2x在x= 处具有极值，求a的值.
2.已知函数f(x)=ax3+bx2-3x在x=1,-1处取得极值讨论f(1),f(-1)是函数f(x)的极大值还是极小值；
学生活动
数学应用
例2.已知函数f(x)=ax3+bx2-3x在x=1,-1处取得极值，
(1)讨论f(1),f(-1)是函数f(x)的极大值还是极小值；
(2)过点A(0，16)作曲线y=f(x)的切线，求切线方程。
例3.已知b>－1,c>0,函数f(x)=x+b的图象与函数g(x)=x2+bx+c的图象相切.
(1)求b与c的关系式(用c表示b ) ;
(2)设函数F(x)=f(x)g(x)在(－∞,＋∞)内有极值点,求c的取值范围.
数学应用
79EX4.f(x)=x3+ax在R上有极值点，则a的取值范围是___.
解：由
有
又f(x)在x=1时取极值，
所以
得a=1或a=-1/2．
当a=1时，
f(x)在R上单调递增，不合题意；
已知函数
在x=1时取得极值, 求实数a的值.
由 得 或 ，
列表如下：
极大值
极小值
+
0
－
0
+
1
当a=-1/2时，
在x=1时取极小值，符合题意．
综上a=-1/2．
10.已知a≠3,求证:函数f(x)=2x3+(a+3)x2+2ax+b有两个不同的极值点.
证明：
令
解得：x1=-1,x2=
当a<3时
x
f(x)
(-∞,-1)
-1
(-1,-a/3)
-a/3
(-a/3,+∞)
＋
0
－
0
＋
↑
极大值f(-1)
极小值f(-a/3)
↑
所以，
当x=-1时，函数f(x)取得极大值
当x= 时，函数f(x)取得极小值
当a>3时同理可证
综上可知，函数f(x)有两个不同的极值点。